1.3. Загальні підходи до опису систем

1.3. Загальні підходи до опису систем

Приклад графічного та аналітичного опису системи. Описуючи систему, найчастіше вдаються до двох способів: графічного (схеми, графи) та аналітичного (математичні вирази, системи рівнянь). Скажімо, схему можна розглядати як графічну модель системи. Від схемного опису можна перейти до аналітичного. При цьому передбачається, що кожний з елементів виконує перетворення, яке було притаманне йому, перш ніж його включили до системи.

Нехай елементи системи  — лінійні перетворювачі; φ і f — перетворювачі, що реалізують відповідно функції φ і f;  — суматори (рис. 1.3).

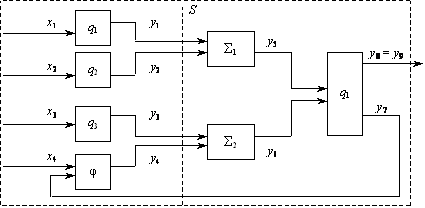
Рис. 1.3. Графічний опис системи

Звідси маємо:

Кількість ступенів свободи системи — це різниця між загальною кількістю змінних та кількістю рівнянь зв’язків між ними. У розглянутому прикладі система має чотири ступені волі.

Динамічний опис систем. Системи, в яких із часом відбуваються деякі зміни, називають динамічними. Стан системи в довільний момент часу можна описати за допомогою набору певних величин — параметрів, що характеризують виходи системи. Зміну станів системи з часом називають рухом сис-
теми.

Описуючи зміну станів та рух системи, застосовують такі способи:

вербальний — послідовно перелічують та описують характеристики стану системи, дістаючи в результаті перше наближення динамічного опису;

графічний — будують діаграми та графіки, що дають наочне уявлення про динаміку процесу в системі;

табличний — подають кількісну оцінку стану системи в дискретні моменти часу;

математичний — записують функціональну залежність стану системи від часу та значень входів системи.

З погляду математики будь-яка динамічна система описує рух точки у так званому фазовому просторі, або просторі станів. Найважливіша характеристика цього простору — його розмірність, тобто кількість величин, які необхідно задати для визначення стану системи. При цьому не так вже й істотно, що це за величини — вони можуть характеризувати кількість різних представників фауни на певній території, або являти собою змінні, що описують сонячну активність чи кардіограму, або подавати частку виборців, які підтримують президента, і т. ін.

Якщо за координатні осі взяти параметри системи, то значення цих параметрів будуть фазовими координатами, а утворений ними вектор z — станом системи.

Кожному стану системи відповідає певна точка фазового простору — зображувальна точка, а кожному процесу зміни стану (руху) системи відповідає певна траєкторія. Сім’ю цих траєкторій називають фазовим портретом системи. Здебіль­шого фазовий портрет являє собою сім’ю неперетинних кри-
вих (рис. 1.4).

Фазова траєкторія, характеризуючи переміщення зображуваль­ної точки, відбиває водночас поводження системи під впливом
деяких факторів. Отже, за допомогою фазової траєкторії можна графічно подавати поводження системи.

Рис. 1.4. Фазовий портрет системи
у двовимірному просторі

Нехай  — функції відповідно входів, виходів та стану динамічної системи, тоді цю систему формально можна описати рівняннями спостереження та стану системи:

,

де f, g — деякі функції.

Коли ці функції та функції зміни входів і виходів неперервні, поводження таких динамічних систем часто описують за допомогою диференціальних рівнянь:

.

Для дискретних систем зміна станів визначається загальним розв’язком рівняння:

.

Розрізняють три характерних типи поводження, або три режими, в яких може перебувати динамічна система: рівноважний, періодичний, перехідний. Рівноважний режим функціонування, або рівновага системи — це здатність її зберігати свій стан як завгодно довго (як за відсутності, так і за наявності зовнішніх збурювальних впливів).

Під стійкістю системи розуміють здатність системи повертатися до стану рівноваги після виведення її з цього стану під впливом зовнішніх збурень. Стан рівноваги, до якого система здатна повертатися, називають стійким станом рівноваги. У складних кібернетичних системах залежно від характеру досліджуваних задач і типу збурень застосовують різні критерії стійкості.

Одним із найбільш поширених є критерій стійкості за Ляпуновим. Стан системи z0 = z(t0) буде стійким за Ляпуновим для всіх , якщо для довільної заданої області допустимих відхилень цього стану  (область  e) існує така область d, що траєкторія довільного руху, яка почалась в області d, не вийде за межі області e, що формально можна записати так:

.

Періодичний режим функціонування системи — це режим, коли протягом рівних проміжків часу система приходить до одного й того самого стану (потрапляє в точку фазового простору).

Перехідним режимом називається рух динамічної системи з одного стійкого режиму (періодичного або рівноважного) до іншого. Швидкість перехідного процесу характеризує інерційність системи.

Усі ці режими характеризують динаміку розвитку соціально-економічних систем. Скажімо, дослідженню рівноважних станів економіки (моделі ринкової рівноваги) та економічним циклам (сезонні цикли, цикли Кондратьєва) приділяється значна увага в економічні теорії. Щодо перехідних (нестійких) режимів функціонування економіки, то останнім часом істотно змінилися погляди на їхню роль в еволюції економічних систем, що посприяло розвитку нових напрямків, зокрема синергетичної економіки (див. розд. 5).

Функція та схема системи. Довільна система має певну функ­цію та схему. Функцією вважатимемо закон перетворення входів сис­теми на її виходи. Схемою назвемо сукупність елементів, що беруть участь у реалізації функції системи, а також структуру їхніх зв’язків.

Очевидно, що таку дійову систему доводиться описувати вже у двох аспектах: з погляду її функцій і дій та з погляду тих методів і засобів, за допомогою яких ці дії реалізовуються. Відповідно така система матиме і дві структури: функціональну та схемну. Зазначену систему можна подати в матричній формі, де найменуваннями рядків будуть елементарні функції, а найменуваннями стовпців — елементарні схеми. Елементи системи міститимуться на перетині рядків і стовпців цієї матриці. Вектор-рядок елементів, пов’язаних із реалізацією певної функції, буде функціональною підсистемою, а вектор-стовпець елементів — схемною підсистемою, що реалізує певний набір функцій.

Такий двовимірний опис системи зручний для будь-яких типів систем. Наприклад, систему управління підприємством або галуззю можна подати, з одного боку, як певний набір функціональних підсистем (планування, керівництва, обліку, матеріального забезпечення), а з другого — як набір схемних підсистем, що відбивають комплекси методів і засобів, за допомогою яких ці функції реалізовуються (інформаційна підсистема, організаційно-правова підсистема, підсистема технічного забезпечення, підсистема математичного забезпечення і т. ін.).

У процесі дослідження систем постають два типи задач.

1. Задача аналізу — за заданою схемою знайти функцію, що її вона реалізовує. Якщо схемна підсистема сама являє собою велику систему, то задача ставиться так: за заданою схемою знайти ієрар­хічну структуру функцій, що їх вона реалізує. Цю задачу можна сформулювати й інакше: за заданою схемою знайти функцію, що реалізовується цією схемою найкраще, тобто знайти оптимальну функцію даної системи.

2. Задача синтезу — за заданою функцією знайти схему, що її реалізує. Якщо функціональна підсистема складна й велика, то необхідно знайти ієрархічну структуру набору схем, що реалізовує дану функцію.

У загальному випадку можна встановити такий орієнтовний порядок опису та роботи із системою:

сформулювати задачу;

обмежити об’єкт дослідження, тобто сформулювати критерії добору елементів системи і скласти список або дати визначення тим підоб’єктам, які включаються до системи; у разі відкритої системи дати також ще один список (визначення) тих об’єктів, що розглядаються як середовище;

визначити ставлення спостерігача до об’єкта;

визначити мову опису системи (тезаурусу, алфавіту, граматики і семантики);

у задачах аналізу на основі спостережень описати схему (структуру) системи та знайти функцію, що реалізовується даною схемою;

у задачах синтезу на основі спостережень описати функцію та знайти схему, що реалізовує дану функцію;

повністю сформулювати систему, тобто знайти відповідність функцій і схем, описавши всі компоненти системи, їхні властивості та взаємозв’язки, що відбиваються у структурі;

подати інтерпретацію результатів, яка полягає у здійсненні перекладу з абстрактної мови системи в більш конкретну, змістов­ну мову опису реального об’єкта.

Для дослідження кожного окремого аспекта системи необхідна відповідна мова опису, яка буде адекватною розв’язанню саме цього аспекта задачі. Для кожного аспекта системи будується своя модель, установлюється взаємозв’язок цих моделей. Кожна з моделей являє собою окрему систему, тому для неї зберігає силу сформульований щойно порядок роботи. Розбіжності виявляються на етапі розгляду складної системи в цілому: для її опису необхідно побудувати об’єднану й розширену метамову, знайти спільну для всіх галузь функціональних або схемних рішень, а в разі розв’язання багатоекстремальної задачі провести операцію послідовної оптимізації.

У роботі зі складною системою неминучі зміщення в послідов­ності етапів роботи, послідовне чергування аналізу і синтезу.

Контрольні запитання та завдання

Охарактеризуйте предмет та методи кібернетики.

Дайте визначення основних понять теорії систем.

Охарактеризуйте місце економічної кібернетики в загальному комплексі економічних наук.

Які методи використовуються в економічній кібернетиці?

Наведіть класифікацію та властивості систем.

У чому полягає динамічний опис систем?

У чому полягають завдання аналізу та синтезу при дослідженні систем?