4.1. Ентропія як міра ступеня невизначеності
4.1. Ентропія як міра ступеня невизначеності
Однією з головних властивостей навколишнього світу та подій, явищ, які в ньому відбуваються, є відсутність повної впевненості щодо їх настання. Це створює невизначеність у плануванні наших дій. Але зрозуміло, що ступінь цієї невизначеності залежно від ситуації випадках буде різною.
У процесі управління економічними системами (наприклад, виробництвом) постійно існує невизначеність щодо стану справ у керованому об’єкті та його дій (поводження) у той чи інший момент. Необхідно знати, як забезпечується виконання встановленої програми, плану дій, які справи з матеріально-технічним, фінансовим, енергетичним, інформаційним забезпеченням. Необхідно також мати вичерпну інформацію щодо стану ринкової кон’юнктури, економічної політики державних органів управління, діяльності конкурентів, партнерів, споживачів тощо. Невизначеність виникає і щодо вибору найбільш доцільного рішення з множини можливих (керувальний вплив). Для того щоб усунути цю невизначеність, необхідна інформація.
На практиці важливо вміти чисельно оцінювати ступінь невизначеності. Розглянемо випробування, яке має K рівноможливих результатів. Зрозуміло, що коли K = 1, результат випробувань не є випадковим і жодної невизначеності немає. Зі збільшенням K невизначеність зростає. Отже, числова характеристика невизначеності f(K) має бути f(1) = 0 і зростати зі збільшенням K. Розглянемо два незалежні випробування α і b. Нехай випробування α має m, а випробування b — n результатів. Добуток подій αb матиме mn результатів. Невизначеність випробування αb буде більшою і від α, і від b.
Природно припустити, що ступінь невизначеності випробування αb дорівнює сумі невизначеностей, які характеризують випробування α і b. Звідси дістаємо таку умову: f(mn) = f(m) + f(n).
Визначимо вигляд цієї функції. Неважко переконатись, що логарифмічна функція y = log(x) — єдина, яка має наведені властивості:
log 1 = 0; log x2 > log x1 при x2 > x1; log(mn) = log m + log n.
Вибір основи системи логарифмів не принциповий, оскільки згідно з формулою logа = logbalogb перехід від однієї основи логарифмів до іншої зводиться до множення на коефіцієнт пропорційності.
У теорії інформації за основу логарифмів беруть число 2, тобто
f(K) = log2(K). Оскільки log22 = 1, то це означає: за одиницю
вимірювання невизначеності взято невизначеність, яка міститься у випробуванні, що має два рівноможливі результати (наприклад, у випробуванні з підкиданням монети).
Така одиниця вимірювання невизначеності називається бітом (bit — binary digit — двійкова цифра).
Розглянемо випробування, що має К рівноймовірних результатів. Тоді таблицю результатів можна подати у вигляді табл. 4.1.
Таблиця 4.1
| Результати | А1 | А2 | … | Аk |
| Імовірність | 1/К | 1/К | … | 1/К |
Оскільки загальна невизначеність випробування дорівнює logK, то можна вважати, що кожний окремий результат вносить у середньому таку невизначеність:
![]() .
.
Щоб обчислити повну невизначеність, знайдемо суму невизначеностей усіх результатів:
![]() .
.
Якщо ж результати випробувань мають різні ймовірності (табл. 4.2), то повна невизначеність буде така:
![]() .
.
Таблиця 4.2
| Результати | А1 | А2 | ………... | Аk |
| Імовірність | P(A1) | P(A2) | ………... | P(Ak) |
Цю величину (за аналогією зі статистичною фізикою) називають ентропією. Отже, ентропія випробування α подається у вигляді
![]() .
.
Властивості ентропії. 1. Н(a) ³ 0 — додатно визначена функція ймовірностей Р(Аi). Справді:
![]() .
.
2. Н(a) = 0 Þ якщо Pj = 1, решта Pі = 0. У цьому випадку невизначеності немає:
![]() , а решта членів
, а решта членів ![]() .
.
3. maxH(a) = max[–SP(Ai)logP(Ai)] = logK при P(A1) = … =
= P(Ak) = ![]() , тобто maxH(a) досягається за рівноможливих результатах.
, тобто maxH(a) досягається за рівноможливих результатах.
Розглянемо два незалежні випробування (табл. 4.3).
Таблиця 4.3
| X | X1 | X2 | … | Xn |
| P | p1 | p2 | … | pn |
| Y | Y1 | Y2 | … | Ym |
| P | q1 | q2 | … | Qm |
Означення. Об’єднанням двох систем X і Y із можливими станами x = {x1, …, xn} і y = {y1, …, ym} називають складну систему (X, Y), стан якої (xi, yj) містить усі можливі значення (комбінації) станів xi, yj систем X, Y.
Очевидно, що кількість можливих станів системи (X, Y) буде nm. Нехай Pij — імовірність того, що система (X, Y) перебуватиме у стані (xi, yj): Pij = P[(X = xi), (Y = yi)] (табл. 4.4).
Таблиця 4.4
|
| x1 | x2 | … | xn |
| y1 | P11 | P12 | … | P1n |
| y2 | P21 | P22 | … | P2n |
| … | … | … | … | … |
| ym | Pm1 | Pm2 | … | Pmn |
За означенням маємо:
![]() ,
, ![]() .
.
Якщо системи X і Y незалежні, то Pij = piqj. Звідси випливає:
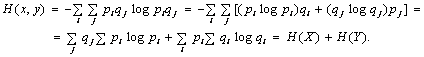
Отже, для незалежних систем виконується рівність: H(X, Y) =
= H(X) + H(Y).
Цей висновок можна узагальнити на скінченну кількість систем: у результаті об’єднання незалежних систем їхні ентропії додаються:
![]() .
.
Умовна ентропія. Нехай маємо дві системи X і Y, які в загальному випадку залежні. Припустимо, що система X набула значення xi. Позначимо через P(yj/xi) умовну ймовірність того, що система Y набуде стану yj за умови, що система X перебуває у стані xi:
![]()
Визначимо умовну ентропію системи Y за умови, що система Х перебуває у стані хi:
![]() (4.1)
(4.1)
де МХi — оператор умовного математичного сподівання величини, що міститься в дужках, за умови Х ~ xi.
Умовна ентропія залежить від того стану xi, якого набула система Х; для одних станів вона більша, для інших менша. Визначимо середню або повну ентропію системи Y, ураховуючи, що система може набувати будь-яких значень. Для цього кожну умовну ентропію (4.1) помножимо на ймовірність відповідного стану Рi, а далі всі такі добутки додамо.
Отже, позначимо повну умовну ентропію через Н(Y / Х). Тоді величина
![]() (4.2)
(4.2)
за означенням буде повною умовною ентропією.
Скориставшись формулою (3.1) та взявши до уваги, що piH ´
´ (Y / xi) = Pij, можна одержати:
![]() . (4.3)
. (4.3)
Величина Н(Y / Х) характеризує ступінь невизначеності системи Y, що залишається після того, як стан системи Х цілком визначився. Її називають повною умовною ентропією системи Y відносно Х.
Для умовної ентропії справджується таке твердження: якщо дві системи Х та Y поєднуються в одну, то ентропія об’єднаної системи буде дорівнювати сумі ентропії однієї з них та умовної ентропії іншої щодо першої:
![]() Н(Х, Y) = Н(Х) + Н(Y / Х); Н(Х, Y) = Н(Y) + Н(X / Y). (4.4)
Н(Х, Y) = Н(Х) + Н(Y / Х); Н(Х, Y) = Н(Y) + Н(X / Y). (4.4)
У частинному випадку, коли системи Х і Y незалежні, тобто
Н(Y / Х) = Н(Y), маємо рівність:
Н(Х, Y) = Н(Х) + Н(Y),
а в загальному випадку виконується нерівність:
Н(Х, Y) £ Н(Х) + Н(Y). (4.5)
Співвідношення (4.5) випливає з того, що повна умовна ен-
тропія не може перевищувати безумовної: Н(Y / Х) £ Н(Y).
Розглянемо інший крайній випадок, коли станом однієї із систем Х цілком визначається стан іншої Y. Тоді Н(Y / Х) = 0, а отже, маємо
Н(Х, Y) = Н(Х) = Н(Y).
Інтуїтивно зрозуміло, що ступінь невизначеності системи не може зрости через те, що стан якоїсь іншої системи став відомим. Зі співвідношення (4.5) випливає, що невизначеність системи, її ентропія досягає максимуму, коли система незалежна.
