4.2. Методи визначення вартості грошової одиниці
4.2. Методи визначення вартості грошової одиниці
Оскільки існують дві складові концепції вартості грошей в часі, відповідно, існують і два способи визначення і нарахування відсотків.
Декурсивний спосіб нарахування відсотків. Відсотки нараховуються в кінці кожного інтервалу нарахування. Їх величина визначається, виходячи з величини капіталу, що надається. Відповідно декурсивна відсоткова ставка (позиковий відсоток) представляє собою виражене у відсотках відношення суми нарахованого за певний інтервал доходу до суми, що є на початок даного інтервалу.
(4.1)
У фінансових розрахунках перший показник ще називається “відсотковою ставкою”, “відсотком”, “ставкою відсотку”, “нормою прибутку”, “доходністю”.
Антисипативний (попередній) спосіб нарахування відсотків. Відсотки нараховуються на початку кожного інтервалу нарахування. Сума процентних грошей визначається, виходячи з нарощеної суми. Відсотковою ставкою буде відношення суми доходу, що виплачується за певний інтервал, до величини нарощеної суми, одержаної по закінченні цього інтервалу (у відсотках).
(4.2)
Визначена таким чином відсоткова ставка називається (в широкому смислі слова) обліковою ставкою, дисконтом або антисипативним відсотком.
Очевидно, що обидві ставки взаємопов’язані, тобто, знаючи один показник, можна розрахувати інший:
або 
Декурсивний спосіб нарахування відсотків є поширеним в світовій практиці; антисипативний метод нарахування відсотків застосовувався в країнах розвинутої ринкової економіки, як правило, в періоди високої інфляції. Але незалежно від способу нарахування відсотків відсоткові ставки можуть бути простими і складними.
Простий відсоток. Простий відсоток – це нарахування відсотку лише на початково інвестовану суму.
Наприклад, на початку року інвестор розміщує на рахунку в банку суму Р під відсоток r. Через рік він одержить суму Р1, яка дорівнює початково інвестованим коштам плюс нараховані відсотки, або
Р1 = Р + Рr = Р (1 + r)
Через два роки сума на рахунку складатиме:
Р2 = Р + Рr + Рr= Р (1 + 2r)
Аналогічно можна представити суму Рn, яку вкладник одержить через n років:
Рn = Р (1 + r n), (4.3)
де: Рn – майбутня вартість;
Р – сьогоднішня вартість.
Приклад
Розрахуйте нарощену суму з вихідної суми в 20000 грн. при розміщенні її в банку на умовах нарахування простих відсотків, якщо річна ставка 15 %, а період нарахування – 10 років.
Нарощена сума складає:
20000 (1 + 0,15 х 10) = 50000 грн.
(Щоб зробити формули більш компактними, відсотки, що нараховуються, беруть одразу в десяткових значеннях, тому замість 15 % ми поставили 0,15).
Нарахування за схемою простих відсотків застосовується, як правило, в короткострокових фінансових операціях, коли інтервал нарахування співпадає з періодом нарахування (і дорівнює строку менше одного року), або коли після кожного інтервалу нарахування кредитору виплачуються відсотки. Природно, що нарахування простих відсотків може застосовуватись і в будь-яких інших випадках за домовленістю сторін, що беруть участь в операції.
Якщо простий відсоток нараховується протягом періоду, який складає менше року, формула (4.3) набуває вигляду:
(4.4)
де: t – кількість днів нарахування відсотку протягом року;
Т – кількість днів в році;
Pt – сума, яка одержується при нарахуванні відсотку за t днів;
r – відсоток, що нараховується.
Якщо не зазначено інше, звичайно нарахований відсоток задається як відсоток в розрахунку на рік. Тоді за t днів буде нарахована тільки його частина, а саме 
або 
.
(4.5)
або
, (4.6)
В формулі (4.5) фінансовий рік складатиме 360, а в формулі (4.6) – 365 днів. Вибір формули (4.5) або (4.6) залежить від того, з яким інструментом працює інвестор. Так, в банківській системі рік вважається рівним 360 дням. Тому розрахунки по нарахуванню відсотків по вкладах потрібно робити за допомогою формули (4.5). Розрахунки по операціях з державними короткостроковими облігаціями здійснюються на базі, рівній 365 дням. В даному випадку використовують формулу (4.6).
В залежності від способу визначення тривалості фінансової операції розраховується або точний, або приблизний (комерційний) відсоток.
Дата видачі і дата погашення позики завжди приймаються за один день. При цьому можливі два варіанти:
використовується точна кількість днів позики, яка визначається по спеціальних таблицях, де вказані порядкові номери кожного дня року; з номеру, який відповідає дню закінчення позики, рахують день першого дня;
береться приблизна кількість днів позики, коли тривалість повного місяця приймається за 30 днів; цей метод використовується, коли не потрібна велика точність, наприклад, при частковому погашенні позики.
Точний відсоток одержують, коли за часову базу беруть фактичну кількість днів в році (365 або 366) і точне число днів позики.
На практиці вибір того чи іншого способу залежить від величини суми, яка використовується при здійсненні фінансової операції.
Приклад
60000 грн. надані підприємству в кредит на 4 місяці з 1.05. ц. р. за ставкою 14 % річних. Необхідно визначити суму кредиту до погашення, якщо нарахування здійснюється з використанням: а) точних відсотків, б) приблизних відсотків.
Сума кредиту дорівнює:
при використанні точного відсотку:
;
при використанні приблизного відсотку:
;
Для порівняльного аналізу фінансові розрахунки необхідно здійснювати на підставі одного часового періоду, тобто 360 або 365 днів. Тому виникає необхідність перерахунку величини відсотку з однієї часової бази на іншу. Це можливо зробити за допомогою формул (4.7) і (4.8):
(4.7)
, (4.8)
де: r365 – ставка відсотку на базі 365 днів;
r360 – ставка відсотку на базі 360 днів.
Приклад
. Визначити ставку відсотку на базі 365 днів.
Відсоткова ставка дорівнює:
В прикладі відсоткова ставка на базі 365 днів дорівнює 15,21 %, а для 360 днів – тільки 15 %. Такий результат одержується в зв’язку з тим, що в першому випадку додатково передбачається нарахування відсотків ще протягом 5 днів.
Якщо період нарахування відсотків вимірюється в місяцях, то формули (4.5) і (4.6) можна представити наступним чином:
, (4.9)
де: t – кількість місяців, протягом яких нараховується відсоток;
Рt – сума, яку інвестор отримає через t місяців.
Приклад
50000 грн. надані підприємству в кредит на шість місяців за ставкою 8 % річних. Необхідно визначити суму кредиту до погашення.
Вона дорівнює:
Складний відсоток: нарахування відсотку один раз на рік
У довгострокових фінансово-кредитних угодах частіше використовують нарахування складних відсотків. При нарахуванні складних відсотків їх нараховують не тільки на основну суму, а й на суму, що включає як основну суму, так і нараховані раніше відсотки. У цьому випадку кажуть, що відбувається капіталізація відсотків в міру їх нарахування.
Відповідно до ідеології нарахування складних відсотків за перший період нарахування відсотків базою для нарахування є основна сума:
Р1 = Р (1 + r)
Відмінність результатів для складного і простого відсотків виникає, починаючи з другого періоду нарахування, оскільки в кінці другого року його капітал зросте до:
Р2 = Р (1 + r) + Р(1 + r) r = Р (1 + r) (1 + r) = Р (1 + r)2
В кінці третього року він складе:
Р3 = Р (1 + r)2 + Р(1 + r)2 r = Р (1 + r)2 (1 + r) = Р (1 + r)3
Аналогічно можна показати, що через n років сума на рахунку зросте до величини:
Рn = Р (1 + r)n (4.10)
Формула складних відсотків є однією з базових формул у фінансових розрахунках, тому для зручності користування значення множника 
, який носить назву мультиплікованого множника і який забезпечує нарощення вартості, табульовані для різних значень r і n (див. додаток 1).
Приклад
250000 грн. інвестовані на 4 роки під 6 % річних. Яку суму одержить інвестор в кінці строку?
Нарахування відсотків декілька разів на рік. Складний відсоток може нараховуватися частіше, ніж один раз на рік, наприклад, раз в півроку, квартал, місяць тощо. Нарахування складних відсотків декілька разів на рік називається компаундингом. Як правило, у фінансових контрактах фіксується річна відсоткова ставка і при цьому відсотки можуть нараховуватися по півріччях, кварталах, місяцях тощо. Відсотки, що нараховуються з певною періодичністю, називаються дискретними. В цьому випадку річна ставка називається номінальною, а відсоткова ставка за один інтервал нарахування вважається рівною відношенню номінальної ставки до кількості інтервалів в році. Нарощена сума буде розраховуватись за наступною формулою:
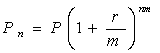, (4.11)
де: m – періодичність нарахування відсотку протягом року.
Приклад
На вклад до банку в розмірі 9000 грн. строком на 5 років банк нараховує 18 % річних. Яка сума буде на рахунку в кінці строку, якщо нарахування відсотків здійснюється за схемою складних відсотків: а) щопівроку; б) щоквартально?
а) 
б) 
Отже, можна зробити висновок, що при фіксованій номінальній ставці є необхідним зазначення частоти нарахувань, оскільки зі зростанням кількості нарахувань відсотків протягом року абсолютний річний доход зростає.
Безперервні нарахування відсотку. Складний відсоток може нараховуватись дуже часто. Якщо тривалість інтервалу нарахування наближається до нуля, а періодичність нарахування відсотків – до нескінченності (m → ∞), ми одержимо безперервне нарахування відсотків, яке нерідко використовується в світовій практиці. Іншими словами, безперервне нарахування відсотків називається нескінченним компаундингом. Не дивлячись на те, що непросто уявити частоту нарахування відсотків, яка дорівнює нескінченності, математично можливо визначити ту суму коштів, яку одержить інвестор, якщо розмістить гроші на умовах відсотку, що нараховується безперервно. Формула для нескінченно нараховуваного відсотку має наступний вигляд:
, (4.12)
де: rn – відсоток, що нараховується безперервно;
n – період часу нарахування відсотку;
е – 2,71828...
Приклад
Знайти нарощену за два роки суму при безперервному нарахуванні відсотків на 500 грн. за ставкою 6 % річних.
Формулу (4.12) можна одержати наступним чином:
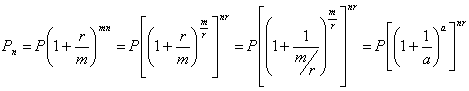
де:
При безперервному нарахуванні відсотків m → ∞ і, відповідно, а → ∞. В даному випадку:
Тоді
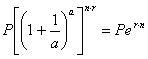
Еквівалентний і ефективний відсотки. В практиці фінансового ринку відсоток, що нараховується по активу, задають як простий відсоток з розрахунку на рік. Однак, якщо в рамках року по активу передбачено нарахування складного відсотку, то загальний результат, який одержить інвестор, буде вище декларованого. Щоб його визначити, необхідно розрахувати ефективний або реальний відсоток.
Ефективний (реальний) відсоток – це відсоток, який одержується за результатами року при нарахуванні складного відсотку.
Ефективний відсоток можна визначити з наступного співвідношення:
, (4.13)
де: rеф – ефективний відсоток;
r – простий відсоток з розрахунку на рік, який заданий за умовами фінансового інструменту.
(4.14)
Приклад
Знайти річну ефективну відсоткову ставку, еквівалентну номінальній ставці 16 % при щоквартальному нарахуванні відсотків.
або 16,99 %
Якщо відомий ефективний відсоток, то за формулою (4.15), яка випливає з формули (4.14), можна визначити еквівалентний йому простий відсоток з розрахунку на рік:
(4.15)
Приклад
, нарахування проводяться раз у півроку. Визначити еквівалентний простий відсоток.
або 14,48 %
Еквівалентність безперервно нарахованого відсотку і відсотку, нарахованого m разів на рік. У фінансових розрахунках може виникнути необхідність знайти еквівалентність між безперервно нарахованим відсотком і відсотком, нарахованим m разів на рік. Наприклад, у формулах визначення курсової вартості опціону використовується відсоток, що нараховується безперервно. В той же час на фінансовому ринку інвестори, головним чином, оперують ставками, що передбачають нарахування відсотку m разів на рік, півроку, квартал і місяць.
Еквівалентність між двома видами відсотків можна знайти, прирівнявши суми, отримані з врахуванням безперервно нарахованого відсотку і нарахування відсотку m раз на рік, а саме:
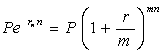, (4.16)
де: rn – безперервно нарахований відсоток
або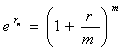 
(4.17)
Звідси
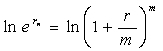(4.18)
або
(4.19)
Приклад
Знайти відсоткову ставку, що відповідає безперервному нарахуванню відсотків, еквівалентну номінальній ставці 12 % при нарахуванні по півріччях.
або 11,654 %
З формули (4.15) відсоток r можна одержати наступним чином:
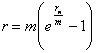(4.20)
Приклад
rn =20 %. Визначити еквівалентний йому відсоток з розрахунку на рік, якщо він нараховується щомісячно.
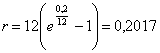або 20,17 %
Комбінація простого і складного відсотків. Досить часто фінансові контракти укладаються на період, що відрізняється від цілої кількості років. В даному випадку відсотки можуть нараховуватись або за схемою складних відсотків (формула (4.10)), або за схемою, яка передбачає нарахування відсотків, що включає і складний, і простий відсотки (за змішаною схемою). Наприклад, кошти вкладника знаходяться на рахунку в банку n років і t днів. Відсотки капіталізуються (тобто приєднуються до основної суми коштів, на яку нараховується відсоток) в кінці кожного року. Протягом року нараховується простий відсоток. Для такого випадку суму, яку одержить інвестор, можна розрахувати за наступною формулою:
, (4.21)
де: Pn+t – сума, яку одержить інвестор за n років і t днів;
P – початково інвестована сума;
t – число днів, за які нараховується простий відсоток;
r – відсоток, що нараховується протягом року.
На практиці в даному випадку часто користуються формулою складних відсотків з відповідними нецілими показниками ступеня. Але потрібно взяти до уваги, що з точки зору сутності нарахування відсотків цей спосіб є приблизним і погрішність при розрахунках буде тим більшою, чим більше значення величин, що входять до формули. Потрібно враховувати, що приблизний метод дає менший, ніж є в дійсності, результат.
Таким чином, в ситуації, коли номінали грошових сум досить високі, від цього методу краще взагалі відмовитися.
Приклад
Нехай 6000 грн. інвестовані на 1 рік і 4 місяці під складні відсотки за ставкою 22 % річних. Знайти нарощену до кінця строку суму а) за схемою складних відсотків; б) за змішаною схемою.
а)
б)
В залежності від того, коли вкладник розміщує кошти на рахунку, простий відсоток може нараховуватись також на початку періоду інвестування коштів або і на початку, і в кінці. Суми, які одержить вкладник, можна розрахувати за допомогою формул (4.22) і (4.23) (капіталізація відсотків здійснюється щорічно):
, (4.22)
, (4.23)
Дисконтована вартість. У фінансових розрахунках виникає необхідність порівнювати між собою різні суми грошей в різні моменти часу.
Щоб порівняти суми грошей в часі, їх необхідно привести до одного часового знаменника. В практиці фінансових розрахунків прийнято приводити суми коштів, які одержить інвестор, до сьогоднішнього дня (початкової точки відліку), тобто визначити величину суми Р, яка в майбутньому повинна скласти задану величину Pn. В цьому випадку Р буде називатись поточною (теперішньою, приведеною) величиною суми Pn.
Теперішня вартість – грошова вартість майбутніх доходів на теперішній час. Розрахунки теперішньої вартості здійснюють за допомогою дисконтування.
Дисконтування – це зведення економічних показників різних років до порівнянного в часі вигляду. Дисконтування здійснюється за допомогою коефіцієнта дисконтування (дисконтуючого множника), в основі якого лежить формула складних відсотків і значення якого також табульовані (див. додаток 2).
Цю задачу вирішують за допомогою формули (4.24), яка називається формулою дисконтованої або приведеної вартості. Вона випливає з формули (4.10):
. (4.24)
де Pn – це майбутня вартість;
Р – дисконтована або приведена вартість (в літературі в якості синонімів використовують також терміни сьогоднішня, дійсна, поточна вартість);
– це коефіцієнт дисконтування. Економічний зміст даного коефіцієнта полягає в тому, що його величина відповідає поточній вартості однієї грошової одиниці, яка буде одержана в кінці періоду n при складному відсотку r. Його величина залежить від тривалості часового періоду і необхідної ставки дисконту.
Формула (4.24) використовується і при оцінці облігацій з нульовим купоном. Оскільки грошові надходження по цій облігації за роками, за винятком останнього, дорівнюють нулю.
Приклад
Визначити поточну вартість облігації з нульовим купоном номінальною вартістю 5000 і строком погашення 12 років, якщо прийнятна норма прибутку складає 14 %.
Vt = 
При нарахуванні складного відсотку m разів на рік формула (4.24) набуває вигляду:
, (4.25)
а для відсотку, що нараховується безперервно:
. (4.26)
На підставі формул (4.24), (4.25) і (4.26) одержуємо відповідно формули дисконтованої вартості для простого відсотку:
. (4.27)
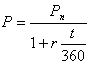. (4.28)
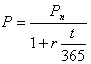. (4.29)
Визначення періоду нарахування відсотків. На практиці виникають питання визначення періоду часу, який необхідний для збільшення суми Р до значення Рn при нарахуванні відсотку r.
Для простого відсотку з формули (4.27) одержимо:
(4.30)
Приклад
За який строк вклад в 8000 грн. збільшиться в 3 рази при ставці 20 % річних?
Приклад
За який строк вклад в 5000 грн. зросте до 13500 грн. при ставці 25 % річних?
Нехай рік дорівнює 365 дням, тоді 0,8 року еквівалентно 
. Таким чином, вклад буде дорівнювати 13500 грн. через 6 років і 292 дні.
З формул (4.28) і (4.29) період t буде дорівнювати відповідно:
