4.3. Рентні платежі (ануїтети) та їх оцінка
4.3. Рентні платежі (ануїтети) та їх оцінка
Визначення майбутньої вартості потоку платежів. Нехай інвестор протягом певного періоду часу в кінці кожного року одержує платежі, які не є однаковими. Якщо він буде інвестувати суму кожного платежу на час до закінчення даного періоду, то після його завершення одержить деяку суму грошей, яку називають майбутньою вартістю потоку платежів.
Майбутню вартість потоку платежів можна визначити за формулою:
, (4.34)
де: F – майбутня вартість потоку платежів;
Ct – сума платежу за рік t;
r – відсоток, під який інвестується сума Ct;
n – кількість років, протягом яких проводяться виплати.
Як видно з формули (4.34), нарахування відсотків на перший платіж здійснюється протягом (n – 1) року, тоді як сама виплата відбувається тільки в кінці першого року.
Приклад
Підприємством були інвестовані кошти на 5 років. В кінці першого року воно одержало 100000 грн., в кінці другого – 200000 грн., третього – 200000 грн., четвертого – 300000 грн., п’ятого – 300000 грн. та інвестувало суму кожного платежу під 30 % річних до закінчення цього п’ятирічного періоду. Визначити майбутню вартість потоку платежів.
100000(1 + 0,3)5-1 + 200000(1 + 0,3)5-2 +200000(1 + 0,3)5-3 +300000(1 + 0,3)5-4 +300000(1 + 0,3)5-5 =1753010 грн.
Майбутня вартість звичайного ануїтету при нарахуванні складного відсотку один раз на рік.
Виникають ситуації, коли отримують (або виплачують) не одну суму, а декілька. Причому виплату (отримання) цих сум проводять за такими правилами: однакова сума через рівні проміжки часу за однієї й тієї самої діючої відсоткової ставки.
Такий механізм припливу (відпливу) грошей одержав назву ануїтету або ренти. Теорія ануїтетів є важливою частиною фінансової математики. Вона застосовується при розгляді питань доходності цінних паперів, в інвестиційному аналізі. Прикладами ануїтету є однакові суми коштів, які перераховують один раз на місяць на депозитний рахунок; однакові суми коштів, які отримують за договором фінансової оренди; однакові щомісячні виплати за кредитом; виплати по облігаціях; премії по страхуванню; регулярні внески до Пенсійного фонду.
Розрізняють два основних типи рент: безумовні й умовні ренти. Безумовні – ренти з фіксованим строком, тобто дати першої і останньої виплати визначені до початку ренти. Умовні – ренти, в яких дата першої та останньої виплат залежить від деякої події. Наприклад, пенсія чи премія по страхуванню життя. Рента називається звичайною або постнумерандо, якщо виплати здійснюються в кінці кожного періоду, і приведеною (авансованою, вексельною або пренумерандо), якщо виплати відбуваються на початку кожного періоду. В зв’язку з тим, що період ренти може співпадати або не співпадати з періодом нарахування відсотків, ренти класифікують на прості і загальні.
Найбільший інтерес з практичної точки зору представляють ануїтети, в яких всі платежі рівні між собою (постійні ануїтети) або змінюються у відповідності до деякої закономірності.
Як і для простої величини, для ануїтету можна визначити його майбутню та теперішню вартість.
Майбутню вартість ануїтету визначають як суму всіх платежів і складних відсотків, що їх нараховують на кожний платіж за період часу, який пройшов від моменту кожного платежу до моменту останнього платежу. Майбутня вартість ануїтету визначається на момент останнього платежу.
Визначити майбутню вартість звичайного ануїтету можливо за допомогою формули (4.34). Однак її можна привести до більш зручного вигляду, так як величина кожного платежу є однаковою. Помножимо обидві частини рівняння (4.34) на (1 + r) і віднімемо одержаний результат з рівняння (4.34). Одержимо:
або
або
(4.35)
Приклад
В кінці кожного року робиться внесок на депозит в сумі 2000 грн. на умовах 9 % річних при щорічному нарахуванні відсотків. Яка сума буде на рахунку через 12 років?
Перетворимо формулу (4.35), щоб одержати значення С:
. (4.36)
Цю формулу можна використати, щоб визначити розмір щорічних відрахувань для формування фонду грошових коштів необхідного розміру, наприклад, пенсійного фонду або фонду по викупу підприємством своїх облігацій.
Приклад.
Підприємство повинно погасити через 3 роки облігації на суму 5000 грн. Визначити розмір щорічних відрахувань для формування викупного фонду, якщо дані кошти до моменту погашення облігації інвестуються під 30 % річних.
Сума щорічних відрахувань складе:
Майбутня вартість звичайного ануїтету при здійсненні виплат m разів на рік. Якщо умови ануїтету передбачають здійснення платежів m разів на рік, то формула (4.34) набуває вигляду:
, (4.37)
де: С – величина виплати за рік.
Помножимо обидві частини рівняння (4.37) на 
і вирахуємо результат з рівняння (4.37). Після перетворення одержимо:
(4.38)
Майбутня вартість ануїтету при нарахуванні відсотку m разів на рік. Випадок, що розглядається, відрізняється від попереднього тим, що складний відсоток нараховується протягом року m разів, а платежі по ануїтету здійснюються тільки в кінці кожного року. Це означає, що відсотки по першому платежу нараховуються з початку другого року і здійснюються m разів на рік; по другому платежу – з початку третього року і також здійснюються m разів на рік тощо.
В даному випадку майбутня вартість ануїтету дорівнює:
(4.39)
Помножимо обидві частини рівняння (4.38) на (1 + r/m)m і вирахуємо результат із рівняння (4.39). Після перетворення одержимо:
(4.40)
Приведена вартість ануїтету при нарахуванні відсотку один раз на рік
Оберненим до поняття майбутньої вартості ануїтету є поняття теперішньої вартості ануїтету. Це – теперішня, поточна або сьогоднішня вартість майбутніх рівномірних платежів, які здійснюють через рівні проміжки часу.
Теперішня вартість ануїтету розраховується шляхом дисконтування на задану ставку і задану кількість періодів, тобто на величину 
:
або
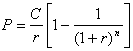, (4.41)
де: Р – приведена вартість ануїтету.
Приклад
В кінці кожного року робиться внесок на депозит в сумі 2000 грн. на умовах 9 % річних при щорічному нарахуванні відсотків протягом 12 років. Визначити приведену вартість ануїтету.
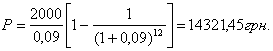
Формулу приведеної вартості ануїтету можна також використати у випадку, коли позичальник бере кредит на умовах його погашення в майбутньому щорічними рівними платежами. Для цього знайдемо з формули (4.41) величину С:
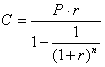, (4.42)
де: P – сума кредиту;
r – відсоток по кредиту;
C – платіж по кредиту;
N – термін кредиту.
Приклад
Ви позичили на чотири роки 10000 грн. під 14 % річних, що нараховуються за схемою складних відсотків на непогашений залишок. Повертати потрібно рівними сумами в кінці кожного року. Визначити величину річного платежу.
Він складе:
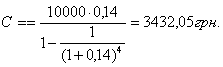
Приведена вартість ануїтету при здійсненні виплат m разів на рік. Для випадку, що розглядається, приведену вартість ануїтету знаходять дисконтуванням майбутньої вартості ануїтету на (1 + r/m)mn.
Тоді
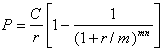(4.43)
Приведена вартість ануїтету при нарахуванні відсотку m разів на рік. Майбутня вартість такого ануїтету розраховується за формулою (4.40). Приведена вартість визначається дисконтуванням правої частини формули (4.40) на (1 + r/m)mn.
Тоді
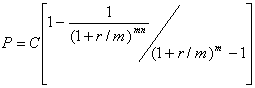(4.44)
Довічна рента. Довічна рента – рента, виплати якої не обмежені ніякими строками. Інша назва довічної ренти – перпетуїтет. Майбутню вартість такого ануїтету визначити неможливо, так як вона не є кінцевою величиною. Однак можна розрахувати приведену вартість довічної ренти, скориставшись формулою (4.41). Оскільки для такого ануїтету n → ∞, то вона набуває вигляду:
(4.45)
Прикладом довічного ануїтету є безстрокові облігації (наприклад, англійська безстрокова державна облігація (консоль), яка випущена у 18 столітті і по ній сплачується дохід кожні півроку) та привілейовані акції, що генерують доход невизначено тривалий час, тому їх поточна теоретична вартість визначається за формулою (4.45).
Найбільш простим варіантом оцінки привілейованої акції є відношення величини дивіденду до ринкової норми прибутку за акціями даного класу ризику (наприклад, ставки банківського проценту за депозитами з поправкою на ризик).
Приклад
Розрахувати поточну ціну безстрокової облігації, якщо річний дохід, що сплачується, складає 100 грн., а ринкова доходність – 12 %.
Vt = 100/0,12 = 833,33 грн.
Таким чином, в умовах рівноважного ринку в даний момент часу облігації даного типу будуть продаватися за ціною 8333,33 грн.
Негайний ануїтет. Ми розглянули звичайний ануїтет, відповідно до якого періодичні та рівномірні платежі здійснюють наприкінці кожного періоду нарахування відсотків.
Існує також авансовий ануїтет (або обернений ануїтет). При авансованому ануїтеті платежі здійснюють не наприкінці кожного періоду нарахування відсотків, а на початку. При цьому кількість платежів однакова, а ось періодів нарахування відсотків на один більше.
Прикладами приведеної ренти є рахунок в банку, земельна рента, премії по страхуванню.
Для розрахунку майбутньої або теперішньої вартості авансованих ануїтетів можна використати формули розрахунку вартості звичайного ануїтету, трохи переробивши їх шляхом множення відповідної величини на (1 + r).
Майбутню вартість ануїтету можна визначити, помноживши формулу (4.45) на (1 + r), так як на кожний платіж відсотки будуть нараховуватися на один рік більше в порівнянні з умовою відкладеного ануїтету.
(4.46)
де: Fn – майбутня вартість негайного ануїтету;
n – кількість років, протягом яких сплачується ануїтет.
Приведену вартість негайного ануїтету знайдемо дисконтуванням правої частини формули (4.46) на (1 + r)n.
Тоді
або
, (4.47)
де: Pn – приведена вартість негайного ануїтету.
Аналогічно рентам з кінцевим строком довічна приведена рента визначається як послідовність періодичних виплат, що здійснюються на початку кожного періоду нескінченно тривалий час.
Приведену вартість негайної довічної ренти можна одержати, помноживши формулу (4.45) на (1 + r).
Тоді
(4.48)