4.3. Розрахунок еластичності попиту за ціною для окремої точки на кривій

Еластичність попиту за ціною можна виміряти для нескінченно малих змін ціни в кожній точці кривої попиту. Необхідність таких розрахунків підтверджується, зокрема, тим, що на одній і тій самій ділянці кривої при застосуванні традиційної методики еластичність буде різною, якщо ціни зростають і якщо вони знижуються. Для прикладу візьмемо таку ситуацію:                   

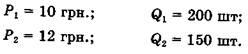
Якщо ціна зросла з 10 до 12 грн., то еластичність попиту буде розраховуватися так:                                       

Якщо ціна зменшилася з 12 до 10 грн., то еластинність попиту буде:

Дещо виправити розрахунки можна, використовую-чи для розрахунку відсоткових змін середні значення ціни та попиту. Однак це не дасть точних результатів для практичного застосування, оскільки еластичність на початку кривої та в її кінці суттєво відрізняється. Ось  чому  потрібно  розраховувати  еластичність для кожної точки кривої попиту.

Припустимо, що маємо справу з лінійною кривою попиту.   Вона  має  постійний  нахил  в  усіх  точках  але не постійну еластичність, яку мозк-

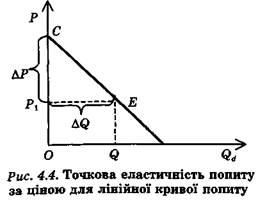
на розрахувати через співвідношення відрізків на осі цін. На рис.

 Тоді розрахунок еластичності попиту за ціною набуде такого вигляду:

Вираз (4.2) називається формулою відстаней, її ви­користовують для розрахунку точкової еластичності.

Отримані результати можуть бути використані та­кож для кривих попиту з нелінійною залежністю. Для цього в точці, де потрібно визначити еластичність, про­водять дотичну до кривої попиту та визначають спів­відношення відрізків на осі цін: відрізка від початку координат до рівня ціни, що відповідає точці на кривій попиту, та відрізка від цього рівня ціни до точки пере­тинання дотичної з віссю цін.