4.5. Оцінка фінансових активів
4.5. Оцінка фінансових активів
Оцінка облігацій з купоном. Грошовий потік в цьому випадку складається з однакових за роками надходжень (С) і номінальної вартості облігації (М), які сплачуються в момент погашення.
(4.64)
де FM2 (r, n) і FM4(r, n) – дисконтуючі множники з фінансових таблиць.
Приклад
Облігація номіналом 500 грн. з піврічним нарахуванням відсотків і купонною ставкою 10 % річних буде погашена через 6 років. Яка її поточна ціна, якщо ринкова норма прибутку 8 %?
Грошовий потік в даному випадку можна представити наступним чином: є 12 періодів; в кожний з перших одинадцяти періодів грошові надходження складуть 25 грн. 
; в останньому періоді, крім 25 грн., інвестору належить ще номінальна вартість облігації. Оскільки ринкова норма прибутку – 8 %, коефіцієнт дисконтування в розрахунку на півроку складе 4 %.
грн.
Оцінка звичайних акцій з рівномірно зростаючими дивідендами. Ціну звичайних акцій з постійними темпами приросту дивідендів знаходять, спираючись на загальну схему оцінки фінансових активів, тобто шляхом складання дисконтованих грошових надходжень від володіння акцією.
Передбачається, що базова величина дивіденду (тобто останнього сплаченого дивіденду) дорівнює С; щорічно вона збільшується з темпом приросту g. По закінченні першого року періоду прогнозування буде сплачений дивіденд в розмірі C x (1+g) тощо. Професор Майрон Дж. Гордон спростив такий підрахунок і довів, що оцінювати вартість акцій з рівномірно зростаючим дивідендом можна наступним чином:
(4.65)
Ця формула має зміст при r > g і носить назву моделі Гордона. Відмітимо, що показники r і g в формулах беруться в частках одиниці.
Приклад
Доходи та дивіденди на звичайні акції фірми щорічно зростали на 6 %. Найближчими роками сподіваються на збереження цих темпів приросту. Останній річний дивіденд становив 2,5 грн. на акцію. Визначити вартість звичайної акції фірми, якщо ставка доходу – 12 %
грн.
Визначення вартості дисконтного векселя. Дисконтні векселі котируються на підставі ставки дисконту. Вона говорить про величину знижки, яку продавець надає покупцю. Ставка дисконту вказується у відсотках до номіналу векселя як простий відсоток в розрахунку на рік. Ставку дисконту можна перерахувати в грошовий еквівалент за допомогою формули:
(4.66)
де: D – дисконт векселя;
N – номінал векселя;
d – ставка дисконту;
t – число днів з моменту придбання векселя до його погашення.
В знаменнику зазначається 360 днів, оскільки розрахунки з векселем здійснюються на базі фінансового року, який становить 360 днів.
Приклад
Визначити величину знижки на вексель номіналом 5000 грн. строком 35 днів, якщо ставка дисконту дорівнює 15 %.
грн.
Ставка дисконту визначається за формулою:
(4.67)
Приклад
Визначити ставку дисконту, якщо номінал векселя – 5000 грн., дисконт векселя – 150 грн. До погашення залишилось 60 днів.
або 18 %
Визначення ціни векселя. Ціну векселя можна визначити, вирахувавши з номіналу величину знижки, а саме:
(4.68)
де: P – ціна векселя.
Якщо відома ставка дисконту, то ціна визначається за формулою:
(4.69)
Приклад
Оцініть поточну вартість векселя номіналом 2500 грн. і строком погашення через 24 дні, якщо ставка дисконту – 9 %.
грн.
Якщо інвестор визначив для себе значення доходності, яку б він бажав забезпечити по векселю, то ціну паперу можна розрахувати за формулою:
(4.70)
де: r – доходність, яку бажає забезпечити собі інвестор. (Якщо вкладник порівнює інвестиції у вексель з іншими паперами, для яких фінансовий рік становить 365 днів, то у формулі доцільно в знаменнику ставити цифру 365).
Визначення суми нарахованих відсотків і вексельної суми за процентним векселем. За процентним векселем нараховуються відсотки за ставкою, яка зазначається у векселі. Суму нарахованих відсотків можна визначити за формулою:
, (4.71)
де: I – сума нарахованих відсотків;
N – номінал векселя;
C% – відсоткова ставка, що нараховується за векселем;
ts – кількість днів від початку нарахування відсотку до його погашення.
Приклад
Номінал векселя дорівнює 2500 грн., за векселем нараховуються 20 % річних, з початку нарахування відсотків до моменту пред’явлення векселя до оплати пройшло 25 днів. Визначити суму нарахованих відсотків.
грн.
Загальна сума, яку держатель процентного векселя отримає при його погашенні, дорівнює сумі нарахованих відсотків і номіналу. Її можна визначити за формулою:
, (4.72)
де: S – сума відсотків і номіналу векселя.
Визначення ціни векселя. Ціна векселя визначається за формулою:
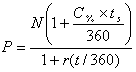, (4.73)
де: P – ціна векселя;
t – кількість днів від купівлі до погашення векселя;
r – доходність, яку бажав би забезпечити собі інвестор.
Визначення суми нарахованих відсотків і суми погашення банківського сертифікату. При погашенні сертифікату інвестор одержить суму нарахованих відсотків, яка визначається за формулою:
, (4.74)
де: N – номінал сертифікату;
I – сума нарахованих відсотків;
C% – купонний процент;
t – строк, на який випущено сертифікат.
Приклад
Сертифікат номіналом 5700 грн. з купоном 30 % був випущений на 70 днів. Визначити суму нарахованих відсотків, які будуть сплачені при погашенні.
грн.
При погашенні сертифікату інвестору також повернуть суму номіналу паперу. Загальну суму, яку одержить вкладник при погашенні сертифікату, можна визначити за формулою:
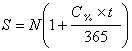, (4.75)
де: S – сума відсотків і номіналу сертифікату.
При погашенні сертифікату із попереднього прикладу інвестор одержить суму, що дорівнює:
грн.
Визначення ціни сертифікату. Ціна сертифікату визначається за формулою:
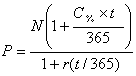, (4.76)
де: P – ціна сертифіката;
t – кількість днів з моменту купівлі до погашення сертифікату;
r – доходність, яку бажав би забезпечити собі інвестор.
Приклад
Сертифікат номіналом 5700 грн. з купоном 30 % був випущений на 70 днів. За якою ціною інвестору потрібно купити сертифікат за 55 днів до погашення, щоб забезпечити доходність 36 %?
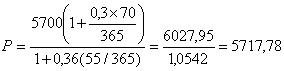грн.