5.1. Вартість грошей у часі
Концепція часової вартості грошей
Час — це гроші! Даний закон конкуренції визначає мотивацію підприємців, а відповідно, і прийняття фінансових рішень менеджерами. Однією з проблем корпорації у її підприємницькій і фінансовій діяльності є проблема нестикування в часі потоків прибутків і витрат. Прибуток ще не накопичено в достатній сумі, але корпорація може прийняти рішення, обумовлене економічними обставинами. Тому вона залучає певні суми для фінансування проекту в борг. Виникає дуже важливе питання: чи виправдане це рішення, тобто «чи варта шкурка вичинки?». Менеджери корпорації мають визначити, чи принесуть позичкові гроші необхідний дохід у майбутньому.
Прийняття фінансових рішень завжди передбачає обмін сьогоднішніх грошей на майбутні гроші. Оскільки купівельна спроможність грошей постійно змінюється, то в кінцевому підсумку відбувається обмін купівельної спроможності сьогоднішніх грошей на купівельну спроможність майбутніх грошей. Процентна ставка, за якою здійснюється цей обмін, залежить від вартості грошей у часі або від тимчасової вартості грошей.
Основи теорії часової вартості грошей викладені американським економістом Ірвінгом Фішером (1867—1947). У своїй праці «Теорія процента», виданій у 1930 р., він розвиває теорію часової вартості грошей. Категорію «час» увів в економіку представник австрійської школи Євген Бем-Баверк (1851—1914). Заслуга І. Фішера полягає в тому, що він на підставі теорії процента показав економічне значення вартості грошей у часі. І. Фішер пише, що «фундаментальна проблема визначення вартості грошей у часі, яку поставила Природа, полягає в приведенні майбутньої вартості до сьогоднішньої, тобто у визначенні капітальної вартості майбутніх прибутків»[1] (курсив наш. — В. С.). І. Фішер підкреслює, що всі інвестори цікавляться майбутніми доходами. Вони об’єднуються для утворення акціонерних товариств і передають функції управління капіталом менеджерам. Основна мета управління корпорацією — максимізація багатства акціонерів, тобто отримання приведеної вартості грошей і, в кінцевому підсумку, нетто приведеної вартості.
Філософською основою розвитку теорії часової вартості грошей є праці лауреата Нобелівської премії І. Пригожина, котрий писав, що «час — фундаментальний вимір нашого існування» і що «час передує буттю»[2]. Прискорення темпів економічного розвитку на основі принципово нових технологій, які «підштовхують час», змусило по-новому глянути на «гроші», інвестовані корпорацією в нові проекти. Вимагалося привести майбутні доходи до «сьогоднішніх грошей».
З 1950-х років, коли загострились економічні проблеми розвитку, інтерес до часової теорії вартості грошей зростає. По-новому постала проблема відновлення капіталу на передовій науково-технічній основі, введення інновацій, нових інформаційних технологій. Потреба збільшення норми накопичення капіталу, її інтенсифікація диктувала необхідність визначення вартості грошей у часі в економічному світі, що швидко розвивається.
Концепція вартості грошей у часі передбачає визначення:
майбутньої вартості грошей;
приведеної (сьогоднішньої) вартості грошей.
Основу концепції часової вартості грошей становить розкриття сутності приведених (сьогоднішніх) грошей.
Як зазначається в західній економічній літературі, концепції тимчасової вартості грошей, а також ризику є основними в теорії і практиці корпоративних фінансів і функціонування ринку капіталу.
По-перше, сьогоднішній долар (євро, єна і т. п.) коштує більше ніж той, який одержить корпорація в майбутньому: через тиждень, через рік. Він сьогодні вже «в роботі», тобто приносить дохід.
По-друге, майбутній долар містить більше ризику, тобто непевності в одержанні очікуваного прибутку, ніж сьогоднішній.
Визначення майбутніх грошових потоків дає можливість обчислити приведену вартість грошей, тобто фінансових потоків, дізнатися, скільки вони коштують сьогодні, зараз. І навпаки, визначення майбутньої вартості дає змогу передбачити рух грошових потоків у майбутньому, тобто їх зростання.
Оцінка майбутньої вартості грошей
Майбутня вартість грошей (Future Value — FV) являє собою суму грошових потоків, яка буде отримана від їх інвестування на певний строк за певною процентною ставкою.
У західній фінансовій літературі підкреслюється, що поняття складних процентів є головним у математичних розрахунках, які стосуються руху фінансових потоків. Оцінка грошових потоків дається в часі. Менеджер постійно аналізує не тільки статику, а й динаміку.
У процесі обчислення майбутньої вартості проценти на певну суму коштів (наприклад, на певний рахунок у банку), отримані за перший рік, додаються до основної суми. За другий рік проценти нараховуються на всю суму, отриману в першому році, і т. д. Отже, проценти нараховуються на проценти отримані. Чим раніше у часі корпорація одержує гроші, тим швидше зростатимуть її майбутні потоки. На практиці це положення змушує менеджерів постійно думати про прискорення оборотності капіталу.
Майбутня вартість визначається за формулою:
![]() ,
,
де FVn — майбутня вартість у n-му році;
х0 — початкова сума капіталу (наприклад, рахунки в банку);
r — процентна ставка (rate).
Для розрахунків звичайно користуються таблицею коефіцієнтів майбутньої вартості або фінансовим калькулятором.
Припустимо, що на рахунку в банку у фірми 10 000 дол., покладені на 10 років з річною ставкою 10 %, тоді
FV = 10 000 · FVIF = 10 000 · 2,5937 = 25 937 дол.
FVIF (Future Value Interest Flow) — майбутня вартість процентних потоків, або процентний фактор майбутньої вартості (за 10 %, терміном на 10 років). Отже, гроші на рахунку зросли за 10 років майже в 2,6 раза, оскільки відбулася капіталізація процентів. Зростання вкладу в банку залежить від його тривалості і процентної ставки.
Майбутню вартість грошей можна обчислити без таблиці і без калькулятора на підставі правила 72. Воно полягає в тому, що кількість років, необхідних для того, щоб сума грошей подвоїлася («час подвоєння»), приблизно дорівнює числу 72, поділеному на процентну ставку:
![]()
Отже, вартість грошей зросте у 2 рази через 7,2 року, тобто дорівнюватиме 20 000 дол., відповідно, через 14,4 року рахунок
у банку зросте до 40 000 дол.[3]
За банківськими депозитами і кредитами процентні ставки встановлюються в річному обчисленні. На практиці використовують різні періоди нарахування процентів (півріччя, місяць, тиждень і т. п.). Для цього ставки приводяться до порівнянної бази через обчислення ефективної процентної ставки EAR (Effective Annual Rate).
Для обчислення ефективної процентної ставки використовується формула:
![]()
де m — кількість періодів нарахування процентів за рік.
Таблиця 5.1
ЕФЕКТИВНІ ПРОЦЕНТНІ СТАВКИ
ДЛЯ РІЧНОЇ ПРОЦЕНТНОЇ СТАВКИ 6 %[4]
| Частота нарахувань | Кількість періодів | Ефективна річна |
| Щороку | 1 | 6,00000 |
| Кожні півроку | 2 | 6,09000 |
| Щокварталу | 4 | 6,13614 |
| Щомісяця | 12 | 6,16778 |
| Щотижня | 52 | 6,17998 |
| Щодня | 365 | 6,18313 |
| Безперервно | Максимальне значення | 6,18365 |
Припустимо, що річна ставка, яка нараховується 2 рази на рік, дорівнює 6 %, тобто кожне півріччя нараховується 3 %. Ефективна процентна ставка становитиме:
![]()
Як видно з таблиці, зростання кількості періодів нарахувань процентів впливає на збільшення ефективної процентної ставки. Вона досягає максимального значення в разі неперервного нарахування процентів, тобто за e = 2,718280,06 = 1,0618365. Тоді
EAR = 1,0618365 – 1 = 0,0618365, або 6,183365 % на рік. Значення е див. у дод. до цього розділу.
Оцінювання приведеної (сьогоднішньої) вартості
Приведена, або сьогоднішня, вартість грошей (Present Va-
lue — PV) являє собою суму грошових потоків, що дисконтуються за певною процентною ставкою.
Припустимо, що фірма може одержати в наступні два роки 10 000 дол. доходу. Якщо взяти найбільш прийнятний ринковий обліковий процент («ціна шансу» — opportunity cost) фондів фірми 8 %, то визначимо, скільки коштує 10 000 дол. сьогодні. З цією метою скористаємося методом дисконтування грошових потоків за формулою:
![]() , або
, або ![]() ,
,
де PVn — сьогоднішня вартість в n-му році;
Х0 — грошовий потік наприкінці n-го року;
r — дисконтна ставка;
![]() — коефіцієнт дисконтування;
— коефіцієнт дисконтування;
FV — майбутня вартість.
Коефіцієнт дисконтування менший 1: ![]() . Це відповідає твердженню, що вартість приведеного долара (євро, єни і т. п.) вища, ніж вона буде в наступному часовому періоді.
. Це відповідає твердженню, що вартість приведеного долара (євро, єни і т. п.) вища, ніж вона буде в наступному часовому періоді.
Першого року сьогоднішня вартість становитиме:
![]()
Другого року:
![]()
Отже, 10 000 дол., отриманих два роки тому, коштують сьогодні менше ніж рік тому. У цьому полягає основна ідея часової вартості грошей. На цьому положенні ґрунтується фінансова й інвестиційна політика корпорації. Фінансові менеджери постійно стежать за рухом цін (курсів) корпоративних акцій і облігацій, за оборотністю активів, реінвестицією прибутку, ціною капіталу, оскільки чим дешевшим буде капітал, залучений корпорацією на фінансовому ринку, тим вища її сьогоднішня вартість. А це, у свою чергу, створює можливість збільшити грошові потоки, вкладені в інвестиційні проекти, які в майбутньому дадуть прибуток. Отже, ціна грошей контролюється як «на вході», так і «на виході», що підтверджує всім відому істину про необхідність обліку грошових потоків — «гроші люблять рахування». Корпорації ведуть облік кожного долара, євро, єни тощо.
Таблиця 5.2
ВАРТІСТЬ КАПІТАЛУ в часі.
ДЕПОЗИТ У БАНКУ 1000 дол. НА 5 РОКІВ, 5 %
| Майбутня вартість | Приведена (сьогоднішня) вартість |
| Future Value (FV) 5 років, 5 % | Present Value (PV) 5 років, 5 % |
| х0 (1 + r)n = 1000 (1 + 0,05)5 = 1000 ´ |
|
| (1 + 0,05)5 = 1,2763 — процентний фактор майбутньої вартості (FVIF) 5 років, 5 % |
|
| Нарахування складних процентів (compounding) | Дисконтування складних процентів (discounting) |
Як випливає з табл. 5.2, приведена (сьогоднішня) вартість — це дисконтована майбутня вартість. Це означає, що якщо для досягнення певної мети корпорації через п’ять років буде потрібно 1276,3 дол., то сьогодні вона повинна мати на рахунку 1000 дол. Припускаємо, що процентні ставки ринку істотно не змінюються. Для визначення майбутньої вартості ми капіталізували проценти, для обчислення сьогоднішньої вартості ми їх дисконтуємо, тобто приводимо вартість грошей у майбутньому до їхньої сьогоднішньої вартості.
Майбутня вартість і сьогоднішня вартість — це дві логічно пов’язані категорії, про що свідчить наведена вище схема (табл. 5.2).
Платежі за боргами, а також різного роду надходження коштів можуть відбуватися рівномірними платежами. Ануїтетами називаються рівномірні платежі корпорації суб’єктам ринку або, навпаки, надходження від них, що здійснюються через однаковий інтервал в однаковій сумі протягом певного періоду. Відомі два методи визначення ануїтетів:
звичайні ануїтети (Ordinary Annuity) — платежі проводяться наприкінці періоду (рік, півроку тощо);
строкові (авансові) ануїтети (Annuity Due) — платежі здійснюються на початку періоду;
безстрокові ануїтети (ренти, консолі), виплата за якими відбувається постійно.
За ануїтетами визначається їх майбутня і сьогоднішня вартість. Особливість полягає в тому, що ануїтет визначається за процентною ставкою на кожний періодичний платіж, потім усі річні суми підсумовуються.
Припустимо, що фірма повинна сплачувати фінансовій інституції чи комерційному банку 10 000 дол. три роки підряд, ануїтет звичайний, тобто платіж відбувається наприкінці періоду.
Фірма—одержувач платежів вкладає отримані суми на поточний рахунок у комерційний банк під 5 % річних. Визначимо щорічні грошові потоки та їх майбутню вартість (див. рис. 5.1).
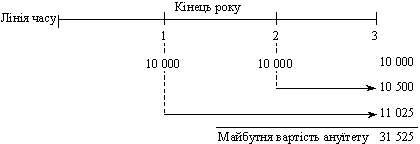
Рис. 5.1. Майбутня вартість звичайного ануїтету
за 5 % річних терміном три роки
Отже, наприкінці терміну, тобто через три роки, грошові потоки становитимуть 31 525 дол. За перший і другий роки визначається майбутня вартість, у третьому році вклад не зросте, оскільки він надійде наприкінці року.
Сьогоднішня вартість звичайного ануїтету за тих самих умов визначається через дисконтування річних платежів.
Отже, до кінця третього року сьогоднішня вартість становитиме 27 232,5 дол., тобто вартість грошей у часі знижується, виявляється дія дисконтного чинника (рис. 5.2).
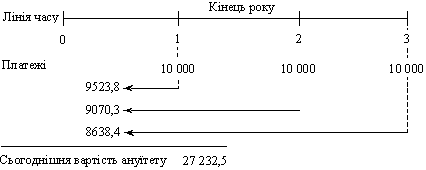
Рис. 5.2. Сьогоднішня вартість звичайного
ануїтету за умови 5 % річних
Безстрокові ануїтети називаються також довічними. Вони були дуже популярні в Західній Європі в XIX ст., в умовах золотого стандарту, коли грошові системи були стійкими. За своєю сутністю привілейовані акції є безстроковими ануїтетами.
Найскладнішою практичною проблемою в часовій вартості грошей є вибір ставки дисконтування r. Ставка дисконтування розглядається як гранична норма дохідності або як альтернативні витрати капіталу. В інвестора є вибір (альтернатива): вкласти гроші у певний проект або купити на фінансовому ринку цінні папери, але він у даному разі віддав перевагу проекту.
Правило норми дохідності полягає в тому, що норма дохідності за інвестиціями повинна перевищувати їх альтернативні витрати.
Сьогоднішня вартість залежить від ставки дисконтування і терміну, на який інвестуються гроші:
чим нижча ставка дисконтування, тобто гранична норма дохідності, тим вища приведена вартість;
чим менший термін, на який вкладено гроші, тим вища приведена вартість.
Звідси виводяться практичні рекомендації: вкладати гроші за найнижчої норми дохідності і на відносно короткий термін, щоб отримати найвищу вартість приведених грошей.
У. Черчіллю приписується фраза: «Той, хто володіє інформацією, володіє світом». Її можна перефразувати, підкресливши значущість інформації для управління фінансами: «Той, хто володіє фінансовою інформацією, володіє фінансовим ринком». Завдання фінансових аналітиків полягає у вивченні руху граничних норм дохідності. Чим успішніша їхня робота, тим ефективніше інвестується капітал корпорації.
Припустимо, що фірма А інвестує 1000 дол. на один рік за ставкою 10 %, фірма Б, що є конкурентом, — за ставкою 9 %, тоді сьогоднішня вартість становить:
для фірми А — ![]()
для фірми Б — ![]()
Далі, фірма А інвестує 1000 дол. на три роки за ставкою 10 %, фірма Б — на два роки за ставкою 9 %, тоді:
для фірми А — ![]()
для фірми Б — ![]()
Отже, фірма Б, що є конкурентом, інвестувала гроші за най-
сприятливіших умов, її сьогоднішня вартість вища, ніж у фірми А.
Графік показує залежність руху очікуваного потоку дивідендів та їх сьогоднішньої вартості в найбільшій американській корпорації «АйБіеМ» (IBM).
За умови рівномірного зростання дивідендів за ставкою 12 % через 15 років дивіденд може зрости до 23 дол. на акцію, але його сьогоднішня вартість буде найнижчою за весь період (рис. 5.3).
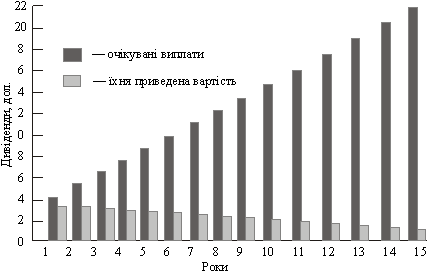
Рис. 5.3. Очікуваний дивідендний потік корпорації «АйБіеМ»
(суми виплат і їх приведеної вартості)[5]
Оцінювання чистої приведеної вартості
Чиста приведена вартість (Net Present Value, NPV) — це різниця між сьогоднішньою вартістю грошових потоків, отриманих від проектних інвестицій, і реальними витратами на здійснення проекту.
Показник чистої приведеної вартості використовується корпорацією для планування капітальних вкладень, тобто інвестування в реальні активи.
Чиста приведена вартість визначається за формулою:
![]() ,
,
де С0 — інвестиції в проект (вхідний грошовий потік);
![]() і т. п. — дисконтовані річні суми припливу капіталу за інвестиціями (результативні грошові потоки).
і т. п. — дисконтовані річні суми припливу капіталу за інвестиціями (результативні грошові потоки).
Коефіцієнт нетто дисконтована вартість показує доцільність очікуваних інвестицій. Якщо дисконтовані грошові потоки інвестування дорівнюють нулю або вищі ніж початкові вкладення за проектом, то менеджери можуть приймати рішення інвестувати в проект. Як уже зазначалося вище, менеджери повинні забезпечити приріст капіталу корпорації. Він може бути досягнутий через збільшення інвестицій у реальні активи і приріст виробленої вартості.
Правила коефіцієнта NPV — інвестувати в проект за позитивного або нульового коефіцієнта.
Припустимо, що корпорація має намір інвестувати в нове інформаційне устаткування 100 млн дол. Очікуваний термін окупності — три роки, гранична ставка дохідності — 15 %. Передбачається, що надходження від проекту в перший рік становитимуть 40 млн дол., у другий — 50 млн дол., у третій — 50 млн дол. Прийняття рішень менеджерами буде визначатися показником NPV.
![]()
= – 100 млн + 34,78 млн + 37,81 млн +
+ 32,89 млн = 5,48 млн > 0.
Менеджери можуть ухвалити рішення про прийняття проекту. Однак вони повинні ще провести додаткові дослідження.
[1] Fisher I. The Theory of Interest. — N.Y.: The Macmillan Company, 1930. — P. 14.
[2] Пригожин И. Конец определенности. Время, Хаос и новые законы Природы. — М.; Ижевск: RAC Dynamics, 2001. — С. 143.
[3] Докладніше про майбутню вартість див.: Боди З., Мертон Р. К. Финансы: Пер.
с англ. — М.: Вильямс, 2000. — С. 158—165.
[4] Там само. — С. 165.
[5] Shapiro A. C. Modern Corporate Finance. — N.Y.: Mac Millan Publishing Company, 1990. — Р. 81.
