5.3. Оцінювання акцій
Оцінювання привілейованої акції
Привілейована акція (Preferred Stock) — гібридна форма цінного папера, що має властивості акції й облігації. Як акція вона підтверджує власність її утримувача на частину майна корпорації. Власник облігації, на відміну від власника звичайної акції, одержує фіксований дохід. У ряді компаній емітуються конвертовані привілейовані акції, власник яких має право обміняти їх на звичайні акції. Привілейована акція випускається як безстроковий цінний папір. Проте є винятки; у такому разі на лицьовому боці акції зазначається її термін. Корпорація має право викуповувати такі акції зазвичай за ціною, вищою номіналу. З цією метою створюється фонд погашення акцій (Sinking Fond). Оцінювання привілейованої акції здійснюється за формулою:
![]()
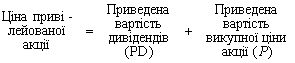 .
.
Привілейована акція більш ризикована, ніж корпоративна облігація, але менше ризикована, ніж звичайна акція. Ця обставина враховується в дисконтній ставці ринкового доходу. Проте привілейовані акції мають деякі податкові переваги, чим користуються інвестори, віддаючи перевагу їхнім корпоративним облігаціям.
Припустимо, що інвестор купує привілейовану акцію з дивідендом 5 дол. щорічно, очікувана облікова ринкова ставка 10 %, корпорація через 5 років викуповує акцію за 30 дол. Визначимо ціну привілейованої акції.
![]()
= 5 · 3,7908 + 30 · 0,6209 = 18,95 + 18,63 = 37,58 дол.
Фінансовий аналітик рекомендує інвестору купити безстрокову привілейовану акцію на тих самих умовах. Її ціна становитиме:
![]()
Ціна акції буде вищою, але прибутковість інвестиції падатиме. У першому випадку вона становитиме ![]() , у другому —
, у другому — ![]() .
.
Звичайна акція (Common Stock у США, Shares — у Великобританії) — цінний папір, що підтверджує власність його утримувача на частину майна корпорації. Фундаментальна ціна звичайної акції визначається дисконтуванням майбутніх доходів, які може отримати її власник. Такими доходами є дивіденди і курсова різниця, які може одержати акціонер, продаючи акції. Для оцінювання акцій застосовується модель дисконтування дивідендів за ринковою дисконтною ставкою або ринковою ставкою капіталізації:
![]() .
.
Оскільки ціна будь-яких безстрокових активів дорівнює майбутнім грошовим потокам, поділеним на дисконтну ставку, то формулу можна спростити:
![]() .
.
Припустимо, що D = 1,82 дол., rs = 16 %, тоді фундаментальна, базисна ціна акції дорівнюватиме:
![]()
Якщо акція буде продана через три роки, то формула виводиться в такий спосіб:
![]() .
.
У даному випадку акція була продана через три роки, отже, до дисконтованих дивідендів додаємо дисконтовану курсову різницю.
Ситуація 1
Припустимо, що корпорація в даний період виплачує дивіденд у розмірі 0,7 дол. Очікується, що наступні чотири роки дивіденди будуть рівномірно зростати на 11 % щорічно. Проте в наступні роки корпорація на певний період припинить виплату дивідендів. Інвестор купив акцію корпорації за 2 дол. Визначте очікувану ціну акції після п’ятого року за дисконтної ставки 12 %.
1. Визначаємо ціну дивідендного доходу:
| Дивіденди (D) |
| PVIF12 % |
| PV | ||||
| D0 | = | 0,7 | ´ | 0,8929 | = | 0,625 | ||
| D1 | = | D0 (1 + 0,11) | = | 0,777 » 0,78 | ´ | 0,7972 | = | 0,6218 |
| D2 | = | D1 (1 + 0,11) | = | 0,8658 » 0,87 | ´ | 0,7118 | = | 0,6193 |
| D3 | = | D2 (1 + 0,11) | = | 0,9657 » 0,97 | ´ | 0,6355 | = | 0,6164 |
| D4 | = | D3 (1 + 0,11) | = | 1,0767 » 1,08 | ´ | 0,5674 | = | 0,6128 |
|
|
|
|
|
|
|
|
| 3,0953 |
2. Визначаємо ціну приросту курсової різниці:
![]() .
.
3. Ціна акції, за якою держатель може її продати після п’ятого року:
3,095 + 0,6213 = 3,72 дол.
Важливою проблемою є визначення r — ринкової дисконтної ставки. Інформаційні фінансові інституції обчислюють ставки за класами цінних паперів. Акціонер звичайної акції може визначити очікувану ставку прибутку за формулою:
![]() .
.
Ситуація 2
Припустимо, що дивіденд останнього року дорівнює 1,82 дол., інвестор купив акцію на вторинному ринку за 11,38 дол., тоді його прибуток становитиме:
![]() .
.
Формула ускладнюється, якщо до неї включається курсова різниця:
![]() .
.
Припустимо, що дивіденд становить 2 дол., поточна ціна акції, за якою інвестор купив акцію, — 14,6 дол. Отже, інвестор може одержати дохід у розмірі ![]() . Далі припустимо, що інвестор продав акцію за 15,1 дол. У даному випадку інвестор отримає дохід:
. Далі припустимо, що інвестор продав акцію за 15,1 дол. У даному випадку інвестор отримає дохід:
![]() .
.
Очікувана ставка доходу зростає, тому що акціонер, продаючи акцію, отримав позитивну курсову різницю. Якщо акціонер продає акцію за 14 дол., тобто нижче ціни придбання (14,0 – 14,6 = –0,6),
то очікувана ставка доходу значно скоротиться:
![]() .
.
Оцінювання звичайних акцій
з постійним темпом зростання дивідендів
Дивіденди на акції можуть щорічно збільшуватися. Якщо вони зростають із постійним темпом, то ціна акції визначається за формулою:
![]() ,
,
де Dt — дивіденд t року, який визначається як D0 (1 + g).
У західній літературі ця формула називається «моделлю Гордона» за іменем американського економіста, котрий увів її в науковий обіг і практику визначення ціни акції.
Ситуація 1
Припустимо, що ми визначаємо ціну акції за темпу зростання дивіденду g = 10 %, процентної ставки — 16 %, D0 = 1,82 дол.
Тоді D1 = D0 (1 + g) = 1,82 (1 + 0,1) = 2,00 дол. Ціна акції становитиме:
![]()
Очікуваний темп зростання дивідендів на практиці у певні періоди може дорівнювати 0, тоді формула оцінки акції трансформується у формулу ціни довічної ренти і буде така: ![]() . Якщо D1 і r є константами (тобто незмінні), то чим вище значення g, тим вища ціна акції.
. Якщо D1 і r є константами (тобто незмінні), то чим вище значення g, тим вища ціна акції.
Ситуація 2
Припустимо, що показник постійного зростання g зріс із 10 до 12 %, а потім — до 13 %. Тоді ціна акції в першому випадку становитиме 73,25 дол., у другому — 97,7 дол.
Попит на такі акції підвищуватиметься, оскільки акціонери, придбаваючи акцію, цікавляться насамперед дивідендами. Виникає питання: чи можливо застосовувати формулу Гордона в тому разі, якщо показник g дорівнює або перевищує процентну ставку r?
З наближенням значення g до значення r модель починає «вибухати», тобто ціна прямує до нескінченності. Тому моделлю можна користуватися тільки у випадках, коли значення g менше значення r.
Було б нереалістичним припускати, що приріст дивіденду протягом тривалого часу не змінюється. Відхилення можливі, але всі вони будуть обертатися навколо очікуваного значення g. Тому формула, як зазначається в західній фінансовій літературі, є однією з кращих у фінансовій практиці для оцінювання акцій.
Оцінювання звичайної акції
з нерівномірним зростанням дивідендів
У періоди економічного розвитку дивіденди зростають, але це зростання може бути нерівномірним. Обчислення ціни акції ускладнюється. Дивіденди корпорацій з надшвидким економічним розвитком (наприклад виробництво комп’ютерів) можуть зростати в перші три-чотири роки піднесення до 30 % за рік, але потім темпи зростання можуть скоротитися до 10 %. Тому ціна акції визначається поетапно. Перший етап — визначаємо сьогоднішню вартість дивідендів у період їх незвичного, бурхливого зростання. Другий етап — обчислюємо сьогоднішню вартість акції в період зниження темпів зростання дивідендів. Оскільки починається
рівномірне зростання дивідендів, то використовується формула Гордона. Третій етап — визначаємо ціну акції, для чого обидва показники складаємо.
Ситуація
Припустимо, що:
rs — ставка доходу, яку сподіваються одержати акціонери (у нашому прикладі — 16 %);
n — роки швидкого зростання дивідендів (три роки);
gs — ставка зростання доходів і дивідендів у період їх швидкого зростання (30 %);
gn — ставка зростання доходів і дивідендів після періоду швидкого зростання (10 %);
D0 — базовий дивіденд (1,82 дол.).
Визначаємо ціну акції:
І. Обчислюємо суму сьогоднішньої вартості дивідендів у період швидкого зростання (за три роки) через послідовні три дії:
1) визначаємо майбутню вартість дивідендів:
D0 · FVIF30 %, t → Dt ;
2) отримане значення дисконтуємо за ставкою 16 %:
Dt · PVIF16 %, t → PV Dt ;
3) підсумовуємо значення наведеної вартості дивідендів за три роки:
D1 = 1,82 · 1,3000 = 2,366 · 0,8621 = 2,040 дол.
D2 = 1,82 · 1,6900 = 3,076 · 0,7432 = 2,286 дол.
D3 = 1,82 · 2,1970 = 3,999 · 0,6407 = 2,562 дол.
Сума сьогоднішньої вартості дивідендів за три роки » 6,89 дол.
PVIF (present value interest factor) — сьогоднішня вартість процентного фактора;
FVIF (future value interest factor) — майбутня вартість процентного фактора.
Показники визначені за відповідними таблицями.
ІІ. Визначаємо ціну акції наприкінці третього року, з урахуванням зниження темпів зростання дивідендів. З цією метою:
а) знаходимо очікувану ціну акції наприкінці третього року:
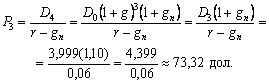
б) знаходимо сьогоднішню ціну акції в третьому році:
![]()
ІІІ. Визначаємо ціну акції з нерівномірним зростанням дивідендів:
![]()
Оцінювання акцій
за допомогою коефіцієнта Р/Е
Коефіцієнт Р/Е — відношення ринкової ціни акції до отриманого доходу після відрахування податків. Коефіцієнт показує, як фінансовий ринок оцінює акцію.
Очікувану ціну акції можна визначити множенням двох коефіцієнтів: доходу на одну акцію, обчисленого для даної корпорації, і Р/Е порівнянної корпорації або середньогалузевої:
![]() .
.
Припустимо, що дохід у розрахунку на одну акцію становить 1,5 дол., а середньогалузевий коефіцієнт Р/Е — 10, тоді очікувана вартість акції корпорації дорівнюватиме: 1,5 ´ 10 = 15 дол.
Ціну акції можна визначити, використовуючи показники прибутку й інвестицій. Інвестиційною політикою корпорації завжди цікавляться інвестори. Акції корпорації, що має високі інвестиційні можливості або ухвалені інвестиційні проекти, користуються великим попитом, навіть за низьких дивідендних виплат.
Якщо припустити, що корпорація не випускала нових акцій, то дивіденди дорівнюють отриманому доходу за мінусом чистих нових інвестицій. Формула для оцінки акції набуває такого вигляду:
![]() ,
,
де Et — дохід, отриманий у році t;
Jt — чисті інвестиції в році t.
Ціна акції дорівнює приведеній вартості її майбутнього доходу за мінусом приведеної вартості майбутніх інвестицій.
Коли ми розглядали модель Гордона, то зазначали, що якщо процент зростання дивідендів перевищує обліковий ринковий процент, користуватися цим методом некоректно. Корпорації, у яких ставка прибутковості за майбутніми інвестиціями перевищує облікову ринкову ставку, називаються корпораціями швидкого зростання, а акції, які вони емітують, швидкозростаючими акціями (growth stocks).
Для оцінювання таких акцій доцільно застосовувати метод оцінювання з використанням реінвестування прибутку.
