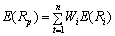6.1. Теорія ризику інвестицій Г. Марковіца
6.1. Теорія ризику інвестицій Г. Марковіца
У даному розділі ми розглянемо поняття ціни капіталу. Корпорація купує необхідний їй капітал на фінансовому ринку, його ціна — позичковий процент.
Для корпорації сплата процента є витратами; чим вища ціна капіталу, тим вищі витрати. Від ціни капіталу залежить прибуток корпорації, який залишається після виплати процентів і податків. Він визначає подальші можливості нагромадження й економічне зростання. Для кредитора корпорації позичковий процент — це дохід; чим вищий процент, тим більший дохід одержує кредитор. На доходи кредитора і, відповідно, на витрати корпорації впливає ризик.
У сучасній економічній літературі вживаються два поняття: невизначеність і ризик, пов’язані з ціною капіталу. Невизначеність — ситуація, за якої неможливо точно передбачити, що буде, наприклад, якщо ціна капіталу підвищується. Ризик — поняття складніше, це ситуація, коли, приймаючи рішення, необхідно враховувати невизначеність, оскільки від цього залежить подальший розвиток корпорації, її добробут. Припустимо, що на ринку складається ситуація, за якої ціна капіталу буде підвищуватися обов’язково, що підтверджується рухом показників ринку капіталів. Менеджери корпорації зобов’язані брати це до уваги, приймаючи рішення щодо емісії цінних паперів. Отже, ризик — це невизначеність у русі майбутніх грошових потоків.
Почнемо виклад теорії ризику з вивчення його статистичного виміру. Коливання доходу акцій або інших цінних паперів, тобто ризик, виражається в тому, що інвестор не отримує очікуваного доходу, або отримує його в розмірі, нижчому від очікуваного.
Ризик вимірюється двома статистичними показниками: дисперсією (variance) і стандартним відхиленням (standard deviation).
Дисперсія (s2) — це середнє значення квадрата різниці між реальною дохідністю акції (портфеля) і середньою дохідністю. Стандартне відхилення визначається як квадратний корінь з дисперсії (![]() ). Обидва показники вимірюють відхилення
). Обидва показники вимірюють відхилення
доходу даного року (місяця і т. д.) від середнього історичного; чим більше відхилення від середньої величини доходу, тим більш ризикованим є інвестування в даний цінний папір.
Наведемо приклад розрахунку дисперсії і стандартного відхилення. Припустимо, що дві гіпотетичні компанії N і M мали таку дохідність своїх акцій за п’ять років:
| Рік | Дохідність компанії N(x) | Дохідність компанії M(x) |
| 1 | –0,18 | 0,04 |
| 2 | 0,40 | 0,08 |
| 3 | 0,28 | –0,10 |
| 4 | 0,10 | 0,09 |
| 5 | 0,07 | 0,11 |
| Σ | 0,67 | 0,22 |
1. Визначаємо середню дохідність за п’ять років (![]() ):
):
Компанія N: 0,67 / 5 = 0,134 або 13,4 %;
Компанія M: 0,22 / 5 = 0,044 або 4,4 %.
2. Визначаємо відхилення реальної дохідності від середньої і квадрат відхилення:
| Рік |
| Квадрат відхилення |
| Квадрат відхилення |
| 1 | –0,314 | 0,099 | –0,004 | 0,000016 |
| 2 | 0,266 | 0,071 | 0,036 | 0,0013 |
| 3 | 0,146 | 0,021 | –0,144 | 0,0207 |
| 4 | –0,034 | 0,0012 | 0,046 | 0,0021 |
| 5 | –0,064 | 0,004 | 0,066 | 0,0044 |
| Σ | 0 | 0,1962 | 0 | 0,028516 |
3. Вимірюємо ризик за цінними паперами: дисперсію (s2) і стандартне відхилення (s):
| Корпорація N | Корпорація M |
| s2 = 0,1962 / 5 = 0,03924 | s2 = 0,02516 / 5 = 0,0057 |
|
|
|
Ситуація
Уявімо, що ви — фінансовий менеджер з формування портфеля інвестицій і вам потрібно вибрати один із двох цінних паперів. Акції К°N приносять вищий дохід, у середньому за п’ять років — 13,4 %, акції К°M дають нижчий дохід — 4,4 %. Високий дохід акцій К°N пов’язаний з вищим ризиком, s дорівнює 19,81 %, тоді як у К°M значення s нижче — 7,55 %. У цьому випадку, якщо компанія проводить агресивну політику на фінансовому ринку, менеджер повинен вибрати акції компанії N. Якщо ж компанія проводить оборонну політику, то краще віддати перевагу акціям компанії M.
Основні принципи теорії Г. Марковіца
Теорію ризику інвестицій на ринку капіталу розробив американський економіст Гаррі Марковіц, основні положення якої були опубліковані в 1952 р. Зауважимо, що до Г. Марковіца великих праць з проблеми, що розглядається, не було. Це можна пояснити браком інформації. Її накопичення відбувалося в умовах швидкого розвитку фінансового ринку, акціонерного капіталу, поглиблення його капіталізації. У цих умовах постали практичні завдання врахування ризику і його можливого подолання, що, у свою чергу, вимагало створення фундаментальної теорії.
Основна концепція Г. Марковіца може бути сформульована так: поведінка учасників ринку капіталу визначається не тільки одержанням очікуваного доходу на свої інвестиції. Вивчення ринку капіталу в США показало, що на всі цінні папери, які обертаються на ринку, є попит. Низькодохідні цінні папери за певних обставин для деяких інвесторів можуть бути більш привабливими, ніж високодохідні. Отже, інвестор визначав свій вибір цінного папера не тільки одержанням очікуваного доходу, а й можливим ризиком. Основною проблемою, яку повинен вирішувати інвестор, є досягнення максимального рівня очікуваної дохідності інвестицій за певного рівня ризику і скорочення можливого ризику за очікуваної дохідності. Мета кожного інвестора — більше доходу за меншого ризику. В американській економічній літературі зазначається, що фінансові аналітики і фінансові менеджери з цінних паперів приділяють цьому питанню багато уваги.
Г. Марковіц, якого вважають батьком сучасної портфельної теорії, запропонував концепцію «оптимального» портфеля інвестицій. Сутність цієї концепції полягає в тому, що в портфелі мають міститися, за можливості, цінні папери всіх видів і модифікацій, вони мають бути різними за термінами, а також емітовані корпораціями різних галузей і географічного положення. Процес формування оптимального портфеля називається диверсифікацією портфеля.
Г. Марковіц запропонував модель диверсифікації, яка широко застосовується на практиці. Її сутність полягає в тому, що диверсифікація здійснюється на основі двох змінних: очікуваної дохідності і стандартного відхилення розподілу дохідності портфеля (тобто можливого ризику). Кожний інвестор повинен підібрати свій власний набір цінних паперів залежно від напряму інвестиційної діяльності. Підбір провадиться методом «проб і помилок», для чого використовуються математичний метод побудови кривих байдужності (Indifference curves).
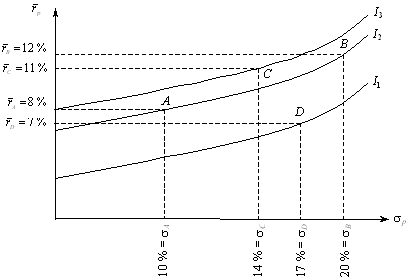
Рис. 6.1. Графік кривих байдужності інвестора, котрий уникає ризику[1]
На горизонтальній прямій (рис. 6.1) відкладені значення стандартних відхилень (sр), на вертикальній — очікувана дохідність ![]() . На підставі аналізу кривих байдужності можна зробити такі висновки.
. На підставі аналізу кривих байдужності можна зробити такі висновки.
Перший — усі портфелі, що містяться на одній кривій байдужності, для інвестора є рівноцінними. Портфель В зі стандартним відхиленням у 20 % більш ризикований, ніж портфель А зі стандартним відхиленням у 10 %. Проте вища очікувана дохідність портфеля В, що становить 12 %, відшкодовує високий ризик, тоді як очікувана дохідність портфеля А становить 8 %.
Другий — для інвестора будь-який портфель, розташований на кривій байдужності вище і лівіше, буде привабливішим, ніж портфель, розташований нижче і правіше[2]. Точки, які розташовані на графіку, показують, що вище і лівіше будуть міститися портфелі більш ризиковані, але і з вищими доходами. Портфель С з більшою очікуваною дохідністю, ніж портфель А, що відшкодовує вищий ризик, тому для інвестора він більш привабливий. Портфель С з меншим стандартним відхиленням, ніж портфель В, що компенсує його меншу очікувану дохідність. Тому портфель С є найбільш привабливим для інвестора. Американські автори вважають, що кожний потенційний інвестор повинен побудувати для свого внутрішнього користування криві байдужності, які б ураховували різні варіанти сполучень очікуваних показників дохідності і стандартних відхилень.
Інвестор може скласти нескінченну множину портфелів. Проте оцінювати всі портфелі йому не обов’язково. Свій оптимальний портфель він мусить вибрати з множини портфелів. З цією метою використовується теорема про ефективну множину (efficient set theorem). На графік з кривими байдужності наноситься рисунок ефективної множини.
На рисунку ефективної множини (заштриховано) точками позначені дохідність і ризик кожної акції (рис. 6.2). Інвестор на підставі своїх переваг може з цих акцій скласти найрізноманітніші портфелі. Область, в якій розташовані точки, називається ефективною множиною (efficient set), а лінія, що графічно її окреслює, — ефективною межею (efficient frontier). Наміри інвестора полягають у тому, щоб очікувана дохідність інвестицій зростала зі зниженням ризику, тому портфелі, що містяться на ефективній межі, будуть оптимальними. При цьому слід зауважити, що ефективний портфель індивідуальний для кожного інвестора. У точці G буде розташований ефективний портфель для інвестора, що очікує мінімальний дохід за мінімального ризику. У точці S міститься ефективний портфель для інвестора, що передбачає максимально високий дохід з максимально можливим ризиком. Можливі численні проміжні варіанти.

Рис. 6.2. Вибір оптимального портфеля[3]
Як показано на рис. 6.2, ефективний портфель буде розташований на одній із кривих байдужності в точці дотику межі ефективної множини. Точка О* на кривій байдужності І2 дотикається межі ефективної множини. Портфель, що міститься в точці О*, буде найефективнішим з усіх портфелів, які можуть бути розташовані вздовж межі ефективної множини. Ця точка найвища і розташована лівіше інших. Теоретично інвестор бажав би, щоб точка дотику містилася на кривій І3, проте в даному варіанті її немає.
Модель Г. Марковіца з практичного погляду в 1950-х роках була мало придатною. Засоби опрацювання інформації тих часів не могли забезпечити швидкого і надійного обчислення ефективної множини й ефективних портфелів. З появою у 80-х роках високопродуктивних комп’ютерів з’явилася реальна можливість розрахунку ефективної множини для кількох тисяч цінних паперів за лічені хвилини. З’являється і відповідна лексика.
Обчислення ефективної множини й ефективного портфеля з допомогою використання комп’ютера називається «оптимізацією», а інвестори застосовують «техніку оптимізації». Проте інвестори часто віддають перевагу використанню певного набору правил і закономірностей. Як зазначають американські автори, «оптимізація» веде до знищення «артистизму і грації» в управлінні інвестиціями. «Оптимізація» не може врахувати історичних подій, надзвичайних обставин. Висновок, якого доходять автори, такий: «Ніщо не може замінити прогноз кваліфікованого спеціаліста про дохідність і ризик цінних паперів, заснований на правильному застосуванні поняття ринкової рівноваги»[4].
Визначення очікуваної дохідності і ризику портфеля
Очікуваний дохід портфеля залежить від очікуваної дохідності кожного цінного папера, що міститься в ньому, та його питомої ваги. Формула очікуваної дохідності портфеля з двох цінних паперів має такий вигляд:
E (Rp) = W1E (Ri) + W2E (Rj),
де E (Rp) — очікуваний дохід портфеля;
Wi і Wj — питома вага цінних паперів у портфелі (W — Weight — вага) за умови, що Wi + Wj = 1;
E (Ri), E (Rj) — очікувані дохідності цінних паперів у портфелі.
Припустимо, що в портфелі дві акції i і j з такими показниками:
| Акція | Очікувана дохідність | σ2 | Питома вага |
| i | 0,078 | 0,0127 | 0,7 |
| j | 0,058 | 0,0034 | 0,3 |
Визначаємо дохідність портфеля:
E (Rp) = 0,078 (0,7) + 0,058 (0,3) = 0,072 → 7,2 %.
Ризик портфеля залежить від питомої ваги кожного цінного папера в портфелі і коваріації їхніх доходів. Формула визначення варіації (мінливості) портфеля:
![]() ,
,
де ![]() — варіація портфеля (вимір ризику);
— варіація портфеля (вимір ризику);
Wi і Wj — питома вага кожного цінного папера в портфелі;
![]() і
і ![]() — варіації (коливання) доходів цінних паперів;
— варіації (коливання) доходів цінних паперів;
sij або Covij — коваріація доходів двох цінних паперів;
2 — коефіцієнт.
Використовуємо ті самі дані, що й за обчислення очікуваного доходу. Додатково нам треба визначити показник коваріації sij за формулою:
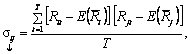
де Т — кількість періодів, використовуваних для визначення коваріації.
Визначаємо стандартне відхилення для кожного цінного папера в кожному році.
2. Визначаємо коваріацію (множимо відхилення від середньої за акцією i на відхилення від середньої за акцією j):
| Рік | Акція i |
| Акція j |
|
|
| 1 | 0,102 | ´ | 0,082 | = | 0,0084 |
| 2 | 0,072 | ´ | 0,032 | = | 0,0023 |
| 3 | –0,208 | ´ | –0,038 | = | 0,0079 |
| 4 | 0,422 | ´ | –0,088 | = | –0,037 |
| 5 | 0,062 | ´ | 0,012 | = | 0,0007 |
| Σ |
|
|
|
| –0,0177 |
3. Визначаємо показник коваріації за п’ятирічний період:
![]() .
.
4. Визначаємо варіацію (мінливість) портфеля:
![]() = (0,7)2 · 0,0127 + (0,3)2 · 0,0034 + 2 · 0,7 · 0,3 · (–0,00354) =
= (0,7)2 · 0,0127 + (0,3)2 · 0,0034 + 2 · 0,7 · 0,3 · (–0,00354) =
= 0,006223 + 0,000306 – 0,0015 = 0,005.
5. Визначаємо стандартне відхилення портфельного доходу (тобто його ризик):
![]() .
.
Можливий другий варіант розв’язання задачі.
Для визначення ризику можна використовувати не тільки показник коваріації, а й коефіцієнт кореляції, які між собою тісно пов’язані.
1. Визначаємо si і sj:
![]() ,
, ![]() .
.
2. Визначаємо коефіцієнт кореляції за формулою:
![]() .
.
3. Вносимо зміни у формулу і визначаємо варіацію портфеля:
![]()
= (0,7)2(0,0127) + (0,3)2(0,0034) + 2(0,7)(0,3) ´
´ (–0,5396)(0,1127)(0,0583) = 0,00622 + 0,000306 +
+ 0,00185 = 0,006529 – 0,001489 = 0,005.
4. Визначаємо ризик портфеля:
![]() .
.
Коефіцієнт кореляції являє собою розщеплену, по суті, зважену коваріацію. Це означає, що коефіцієнт кореляції коливається від +1 до –1. Якщо коефіцієнт кореляції більший 0, то це означає, що дві змінні (у даному разі доходи за двома акціями) змінюються в одному напрямку. Портфельний ризик буде залежати від ризику кожної акції та її питомої ваги в портфелі. Чим менша тіснота зв’язку між рухом доходів від акцій, тим нижчий можливий ризик. У випадку, коли коефіцієнт становить –1, рух доходів за акціями відбувається в різних напрямках. Інвестор звичайно прагне створити портфель з нульовою варіацією через регулювання частками акцій у ньому.
Дохідність і ризик портфеля з множиною цінних паперів визначаються за формулами: