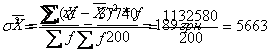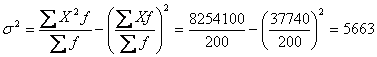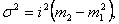6.2. Абсолютні показники варіації: економічний зміст та способи обчислення
Для вимірювання та оцінки розміру варіації використовується система абсолютних показників, які розглядаються як абсолютна міра варіації:
1. Розмах варіації (R), що характеризує максимальну амплітуду коливань значень ознаки у сукупності:
R = xmax – xmin,
де xmax, xmin — відповідно найбільше та найменше значення ознаки
сукупності.
В інтервальних рядах розподілу розмах варіації визначається як різниця між верхньою межею останнього та нижньою межею першого інтервалу. Перевагою даного показника є простота обчислення та ясність економічної інтерпретації. Головний недолік полягає у тому, що він визначається по двох граничних величинах, які часто є випадковими.
2. Середнє лінійне відхилення (l), що характеризує середній розмір коливань значень ознаки навколо середнього рівня:

Просте середнє лінійне відхилення визначається по індивідуальних даних, а зважене — в рядах розподілу. В інтервальних рядах розподілу спочатку знаходиться середина кожного інтервалу, а далі робляться обчислення за наведеною формулою.
![]()
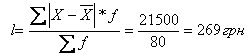
3. Дисперсія (σ2) — це середній квадрат відхилень значень ознаки від середнього рівня:

Для полегшення підрахунків використовують формули:
В інтервальних рядах розподілу для знаходження дисперсії спочатку визначається середина кожного інтервалу.
В інтервальних рядах розподілу з рівними інтервалами дисперсію можна визначити методом «моментів» за формулою:
![]()
де

і — величина інтервалу.
Приклад розрахунку:
|
|
Число сімей |
Серед. інтер. |
х–А, А = 325 |
(х–А)/і і = 50 |
|
|
|
| 100–150 | 5 | 125 | –200 | –4 | –20 | 16 | 80 |
| 150–200 | 15 | 175 | –150 | –3 | –45 | 9 | 135 |
| 200–250 | 10 | 225 | –100 | –2 | –20 | 4 | 40 |
| 250–300 | 20 | 275 | –50 | –1 | –20 | 1 | 20 |
| 300–350 | 17 | 325 | 0 | 0 | 0 | 0 | 0 |
продовження таблиці
| 350–400 | 23 | 375 | 50 | 1 | 23 | 1 | 23 |
| 400–450 | 8 | 425 | 100 | 2 | 16 | 4 | 32 |
| 450 і більше | 2 | 475 | 150 | 3 | 6 | 9 | 18 |
| Разом | 100 | х | х | х | –60 | х | 348 |

Момент першого порядку:
Момент другого порядку:
Дисперсія

4. Середнє квадратичне відхилення (σ) — показує, на скільки в середньому відхиляються значення ознаки від середнього рівня:
![]()
Наприклад, на основі попередніх підрахунків середнє квадратичне відхилення місячного доходу становить:
![]()
Середнє квадратичне відхилення найчастіше використовується у статистичному аналізі, тому його називають стандартним відхиленням. Зрозуміло, що чим меншою є його величина, тим слабкішою є варіація і більш однорідною - статистична сукупність.