6.3. Ізоморфні та гомоморфні системи
6.3. Ізоморфні та гомоморфні системи
Ізоморфними системами з погляду кібернетичного моделювання називаються системи, однакові для спостерігача, якому доступні лише входи та виходи цих систем.
Отже, умовою ізоморфності систем А і В є така система рівностей для довільного елемента (моменту часу) t:
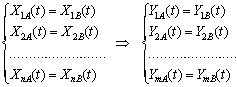
Тут ізоморфізм тлумачиться як ідентичність поводження розглядуваних систем у деякому середовищі, з яким вони контактують через свої входи та виходи. При цьому системи А і В можуть мати різну фізичну природу. Ізоморфні системи є ідеальними
функціональними моделями одна одної.
Гомоморфізм. Нехай маємо дві системи, структуру яких ілюструє рис. 6.2.

Рис. 6.2. До означення гомоморфізму
При цьому залежність між входами та виходами має вигляд:
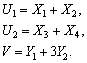
У такому разі системи А і В уже не будуть ізоморфними, та й структура в них різна: модель Y «простіша», має менше входів і виходів. Але зауважимо таке: для кожного стану системи А маємо тільки один цілком визначений стан системи В, тобто за станом системи А ми однозначно можемо визначити стан системи В.
Наприклад, якщо значення параметрів для системи А буде
{Х1 = 1, Х2 = 3, Х3 = 5, Х4 = 2, Y1 = 7, Y2 = 4}, то для системи В дістанемо {U1 = 4, U2 = 7, V = 19}.
Але якщо ми задамо якийсь стан системи В, то однозначно визначити стан системи А не зможемо — у системи А можлива множина станів. Наприклад, якщо для системи В маємо {U1 = 5, U2 = 4, V = 10}, то для системи А дістанемо 6 змінних і 3 рівняння:
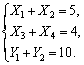
Отже, система А не буде однозначно визначеною. Таку відповідність називають гомоморфізмом (рис. 6.3).

Рис. 6.3. Гомоморфні системи
Нехай система А — оригінал. Для цієї системи побудуємо модель В. Система А має розмірність n, а В — розмірність m < n. Якщо при цьому кожному стану А відповідає один цілком визначений стан B, але не кожному стану B відповідає один стан А, то систему В називають гомоморфною моделлю системи А.
Взагалі, створюючи модель В системи А ми намагаємося, як правило, втілити в цій моделі найбільш істотні властивості системи А, відкидаючи множину менш істотних властивостей з метою спрощення моделі. У результаті цього спрощення розмірність моделі В завжди буде меншою за розмірність А (тобто m < n).
Отже, модель — це гомоморфний образ оригіналу.
Модель «чорної скриньки» у вивченні великих економічних систем. З погляду «чорної скриньки» системи, що мають однакові входи та виходи й однаково реагують на зовнішні впливи, є ізоморфними, хоча за внутрішньою структурою вони можуть бути різними.
Модель «чорної скриньки» незамінна під час вивчення великих, зокрема й економічних систем. Зауважимо, що докладно вивчати поводження таких систем, впливаючи на їхні входи та спостерігаючи за виходами, як правило, неможливо, оскільки потребувало б надто багато часу. Навіть тоді, коли б ми мали у своєму розпорядженні всю інформацію про стан усіх елементів системи, навряд чи можна було б скласти повне уявлення про її поводження. Адже за величезної кількості зв’язків між елементами наявну інформацію не вдається звести в єдине ціле.
У цьому разі потрібно реальну складну економічну систему замінити іншою, простішою, але такою, що функціонує аналогічно. Отож економічну систему розглядають як «чорну скриньку»
і будують її спрощену модель, причому сама «чорна скринька» і модель, що її відтворює, описуються однаковими математичними співвідношеннями.
За такого абстрагування однозначним перетворенням реальної економічної системи дістають простішу модель, вилучаючи неістотні змінні, з певним наближенням оцінюючи значення істотних змінних, апроксимуючи нелінійні та стохастичні залежності лінійними й детермінованими, і т. ін. Здобута модель буде гомоморфною і, якщо зроблені припущення є достатньо обґрунтованими, то й адекватною моделлю складної реальної економічної системи.
Завдяки спрощенню реальної системи дістаємо однозначну відповідність її стану гомоморфній моделі, а також неоднозначність оберненої відповідності.
