6.4. Графічний аналіз ціни капіталу і ризику
6.4. Графічний аналіз ціни капіталу і ризику
Лінія ринку капіталу (The Capital Market Line — CML) відтворює графічно рівняння:
.
Отже, лінія ринку капіталу являє собою пряму лінію з позитивним нахилом, що показує рівновагу між загальним ризиком і дохідністю повністю диверсифікованого портфеля цінних паперів.
Точка М (рис. 6.4) демонструє рівновагу між ризиком ринкового портфеля sm і його дохідністю Rm. У точці М кут нахилу лінії ринку капіталів можна виразити як
, що є коефіцієнтом винагороди за ризик. Очікувана дохідність портфелів Pi і Pj вища ринкового портфеля Rm, відповідно, ці портфелі матимуть вищий ризик spi і spj і вищі премії за ризик: (Rpj – Rf) і (Rpi – Rf).
Коефіцієнт винагороди за ризик (премія за ризик) у портфелів Pi і Pj буде однаковим, тому всі вони будуть розташовані на лінії ринку капіталів. Передбачається, що не тільки портфель Pj матиме найвищий дохід, а і його премія за ризик буде вищою. Відповідно, портфель Pi, мабуть, одержить дохід нижчий, але і премія за ризик у нього буде нижчою.
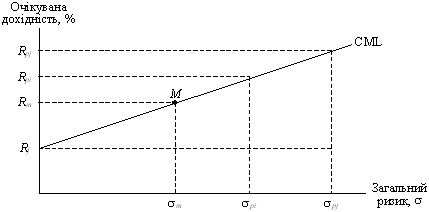
Рис. 6.4. Лінія ринку капіталу
Припустимо, що безризикова процентна ставка становить 7 %,
sm ринкова — 0,22, sp цінних паперів i — 0,20, цінних паперів j — 0,26, g — 0,22. Очікувана процентна ставка ринкового портфеля — 16 %. Потрібно визначити очікувану дохідність за кожним цінним папером.
1) 
;
2) 
;
3) 
.
Отже, очікувана дохідність портфеля цінних паперів i становить 15,1 %, що нижче ринкової. Дохід портфеля j зі ступенем ризику, вищим від ринкового, може принести інвестору дохід, вищий ринкового, в розмірі 17,6 %. Портфель g з ризиком, рівним ринковому, принесе дохід також рівний ринковому.
Лінія ринку цінних паперів, яка ще називається лінією стану фондового ринку (The Security Market Line — SML), графічно відтворює рівняння Шарпа:
.
Отже, лінія ринку цінних паперів являє собою пряму лінію з додатним нахилом, що показує рівновагу між систематичним ризиком і дохідністю певного цінного папера (або портфеля цінних паперів). У літературі відзначається універсальність лінії стану фондового ринку.
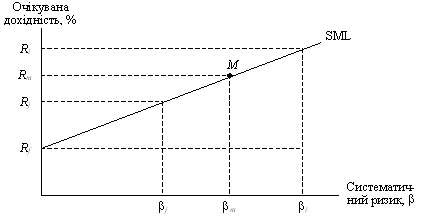
Рис. 6.5. Лінія ринку цінних паперів
Точка М (рис. 6.5) показує рівновагу між систематичним ризиком цінного папера (або портфеля) і ринковою β, що дорівнює 1.
Усі точки, що виражають лінійне відношення між β й очікуваним доходом за цінним папером (портфелем цінних паперів), будуть розташовані на лінії ринку цінних паперів. Тому премія за ризик становить:
.
Якщо інвестор володіє цінним папером (або портфелем цінних паперів) з β = 1, то він фактично володіє ринковим портфелем.
Припустимо, що безризикова процентна ставка дорівнює 7 %, b за цінним папером j — 0,5; за цінним папером i — 1,5; за цінним папером g — 1; очікувана ставка ринкового портфеля — 16 %. Визначимо очікувану дохідність за кожним цінним папером:
1) 
;
2) 
;
3) 
.
Інвестори проводять політику на ринку капіталів відповідно до своїх мотивацій. Ті з них, які намагаються не ризикувати, одержують дохід нижчий ринкового, інші йдуть на високий ризик, сподіваючись одержати високий дохід. У першому випадку інвестор проводить оборонну політику, у другому — агресивну.
Отже, цінний папір за оборонної політики може принести інвестору дохід у розмірі 11,5 %, що нижче ринкового; за агресивної політики — 20,5 %, тобто вищий ринкового. Цінний папір з β = 1 принесе дохід, рівний ринковому, тобто 16 %.
Обидві лінії, розглянуті нами, мають ту саму мету: визначити очікуваний дохід фінансового активу з урахуванням ризику. Проте між ними є відмінності:
По-перше, лінія ринку капіталів заснована на використанні показника загального ризику (стандартного відхилення — s), тоді як лінія ринку цінних паперів — на використанні систематичного ризику (b).
По-друге, лінія ринку капіталів виражає рівновагу між ризиком і доходом повністю диверсифікованого портфеля, тоді як лінія ринку цінних паперів виражає рівновагу будь-якого портфеля цінних паперів, а також окремого цінного папера.
По-третє, на лінії ринку капіталів розташовані всі повністю диверсифіковані портфелі, тоді як окремі цінні папери будуть міститися нижче лінії. На лінії ринку цінних паперів розташовані всі портфелі і цінні папери.
Лінія характеристики цінного папера
Лінія характеристики цінного папера (The Characteristic Line of a Security) графічно відтворює рівняння регресії:
E(Ri)t = ai + biRmt + eit,
де E(Ri)t — дохід за цінним папером i у період t;
Rmt — дохід ринкового портфеля в період t;
ai — параметр точки перетину лінії характеристики осі абсцис;
bi — параметр коефіцієнта нахилу лінії характеристики цінного папера;
eit — випадкові помилки.
Лінія характеристики цінного папера являє собою пряму лінію регресії доходу цінного папера (або портфеля) відносно доходу ринкового портфеля, який зазвичай виражається певним індексом. Американські аналітики переважно використовують індекс Стендард енд Пур’з 500 (рис. 6.6).
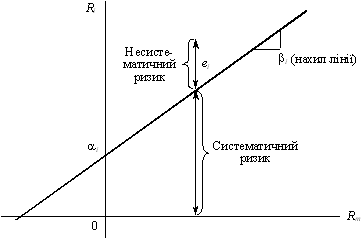
Рис. 6.6. Лінія характеристики цінного папера[1]
У рівнянні лінія характеристики a показує ступінь зміни ціни на акцію i у процентах щодо зміни ринкових цін m за певний період t. Показник a може бути як позитивним, так і негативним. Позитивне значення a показує зростання дохідності цінного папера відносно ринкового доходу. Негативне значення a показує зниження дохідності цінного папера відносно ринкового доходу. У цьому випадку інвестори на ринку в цілому нічого не зароблять.
В умовах рівноваги цін a прагне до 0. На графіку a є точкою перетину лінії характеристики і лінії абсцис, на якій показані доходи, що приносить цінний папір i (Ri) або портфель (Rp).
Коефіцієнт b показує нахил лінії характеристики. Якщо b = 1,
то a = 0. У випадку, коли b > 1, політику інвестора можна визначити як агресивну, тобто виявляється прагнення до більшої ризикованості з метою одержати великий дохід. Тут a буде додатна, оскільки спостерігатиметься зростання дохідності цінного папера відносно ринкового доходу. У разі від’ємної a зниження дохідності може призвести до зниження коефіцієнта b. З цих теоретичних рівнянь і графіків виходить визначення інвестиційної політики інвесторів. Цінний папір з надлишковою дохідністю, тобто коли a додатна, є привабливішим, ніж коли вона від’ємна, тоді як цінні папери з b, вищою ринкової, є менш привабливими, ніж з більш низькою b. Звідси виникає неписане правило для інвесторів: тримай a за цінним папером високою, а b — низькою (Keep your a high, your b low).
Відхилення від середньої квадратичної, що розташована вище лінії характеристики, називається помилкою регресії (the error of regression — eit) (рис. 6.6) і в даному випадку показує несистематичний ризик за цінним папером. Чим більше відхилення, тим вищий систематичний ризик за інших рівних умов. У західній фінансовій літературі зазначається, що застосування техніки оцінки стандартного відхилення розташування понад лінію характеристики показує, що помилка регресії дорівнює 0. Зведення в квадрат означає, що додатне і від’ємне відхилення належать (relevant) до систематичного ризику[2]. Звідси виводиться формула чинника ризику цінного папера за постійної ai:
,
тобто
.
Ситуація
Фінансовий аналітик одержав завдання визначити: 1) коефіцієнти a і b для акції корпорації, яка виробляє радіотелефонну апаратуру; 2) систематичний і несистематичний ризик у загальному ризику. Отримано інформацію:
Дисперсія:
ринку акцій даного класу
;
акції компанії 
.
Середня дохідність:
ринку акцій даного класу 
;
акції компанії 
.
Коваріація дохідності ринку й акції (Covim) = 0,00119.
Рівняння регресії:
(en у цьому прикладі ігноруємо).
Розв’язання
1) 
;
2) 
= 0,01551.
На підставі розрахованих коефіцієнтів будуємо графік лінії характеристики цінного папера i (рис. 6.7).
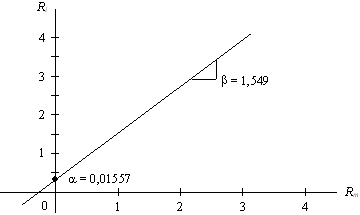
Рис. 6.7. Лінія характеристики цінного папера
З цією метою визначаємо коефіцієнт кореляції ризику дохідності ринку m та акції i:
.
Розраховуємо:
1) стандартне відхилення:
; 
; 
;
2) коефіцієнт 
;
3) коефіцієнт детермінації: 
.
Коефіцієнт детермінації показує, що 37,24 % мінливості доходу за цінним папером визначаються рухом ринкового індексу, тобто мінливістю ринкового доходу.
Визначаємо частки систематичного і несистематичного ризику в загальному ризику, взявши за показник загального ризику дисперсію (s2):
;
0,00493 = 0,3724 · 0,00493 + (1 – 0,3724) · 0,00493 =
= 0,00183 + (0,6277) · 0,00493 = 0,00183 + 0,00310 = 0,00493.
Отже, 37,2 % у загальному ризику становить систематичний ризик; 62,8 % — несистематичний.