6.5. Структурні середні – мода і медіана
Для характеристики розподілу одиниць сукупності за певною ознакою використовується так звані порядкові або структурні середні — мода і медіана.
Мода (М0) — це значення ознаки, що найчастіше зустрічається у сукупності. Таким чином, у дискретному ряді розподілу - це варіанта, що має найбільшу частоту. В інтервальному ряді розподілу мода знаходиться за формулою:
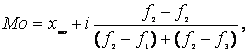
де: хмо — нижня межа модального інтервалу;
і — величина модального інтервалу;
f2, f1, f3 — відповідно частота модального, передмодального та після модального інтервалів.
Слід мати на увазі, що в інтервальних рядах розподілу з нерівними інтервалами модальним вважається інтервал з найбільшою щільністю розподілу, а мода дорівнює його середині.
Медіана (Ме) — це значення ознаки, що ділить рангований ряд значень показника на дві рівні частини. У першої половини одиниць значення ознаки менше медіани, а у другої — більше. Тобто, медіана — це серединне значення.
У тому випадку, коли відомі індивідуальні значення ознаки, їх спочатку рангують (розміщують в порядку зростання чи спадання). Потім визначають номер (місце) медіани:
![]()
При непарній кількості одиниць медіана дорівнює значенню ознаки з порядковим номером (n + 1)/2 . При непарній кількості одиниць медіана визначається як півсума двох значень — з порядковими номерами n/2 та (n + 2)/2.
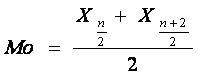
Наприклад, маємо ранговий ряд росту студентів (см):
163, 165, 167, 168, 171, 174, 175, 178, 180, 185, 187, 190.
Номер медіани: (12 + 1)/2 = 6,5. Отже, медіана — це півсума 6-го та 7-го значення:
![]()
Таким чином, половина студентів має зріст менше 174,5 см, а половина — більше, ніж 174,5 см.
В інтервальному ряді розподілу медіана визначається за формулою:
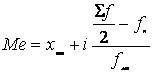
де хме — нижня межа медіанного інтервалу;
і — величина інтервалу;
fн — нагромаджена частота передмедіанного інтервалу;
fме — частота медіанного інтервалу.
Приклад розрахунку моди і медіани для інтервального ряду розподілу:
| Розмір штрафу, грн. | Число штрафів | Нагромаджена частота (fн) |
| До 100 | 4 | 4 |
| 100-200 | 20 | 24 |
| 200-300 | 26 | 50 |
| 300-400 | 15 | 65 |
| 400-500 | 8 | 73 |
| 500-600 | 3 | 76 |
| 600-700 | 2 | 78 |
| 700 і більше | 2 | 80 |
Мода дорівнює:
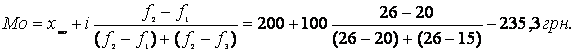
Медіана становить:
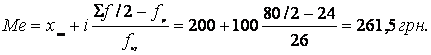
Таким чином, найчастіше розмір штрафу становить 235,3 грн, половина штрафів менше 261,5 грн, а половина — більше.
