7.5. Характеристики форми розподілу
При вивченні форми розподілу в залежності від значень частот розрізняють одно-, дво- та багатовершинні ряди розподілу. Якісно однорідні сукупності мають одновершинний (одномодальний) розподіл одиниць. Наявність декількох вершин свідчить про неоднорідність сукупності.
Серед одновершинних рядів розподілу розрізняють симетричні та несиметричні, госто- та плосковершинні. У симетричних рядах розподілу середня арифметична, мода і медіана співпадають.
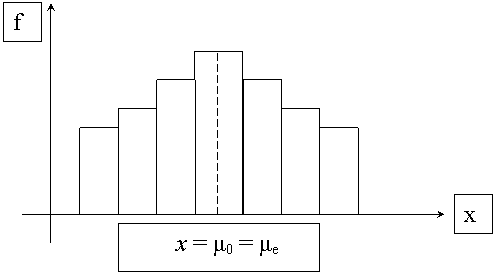
В асиметричних рядах розподілу вершина зміщена вправо або вліво, а напрямок асиметрії є протилежний до зміщення вершини. Так, при правосторонній асиметрії:
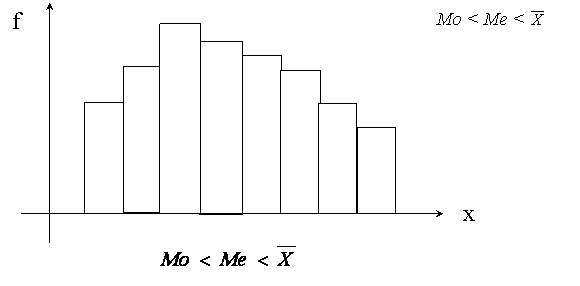
При лівосторонній асиметрії:
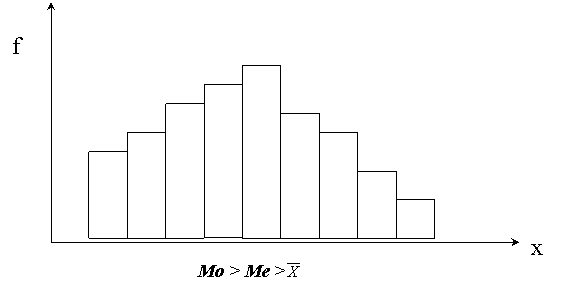
Напрямок та міру асиметрії характеризують коефіцієнти асиметрії, які обчислюються за формулами:
При правосторонній асиметрії А > 0, при лівосторонній А < 0, при симетричному розподілі А = 0. Вважається,
що при |A| < 0,25 асиметрія слабка, при 0,25<|A| <0,5 – середня, при |A| > 0,5 - сильна.
Наприклад, якщо σ = 24,6; X = 180,5; Мо = 164,4; Ме = 170,1 коефіцієнти асиметрії становлять:
Одержані результати свідчать про наявність сильної правосторонньої асиметрії.
Коефіцієнт асиметрії можна також визначити за формулою:
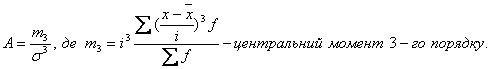
При дослідженні ступеня концентрації одиниць навколо середнього рівня визначають коефіцієнт ексцесу:
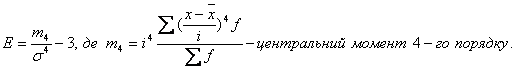
При гостровершинному розподілі Е > 0, при плосковершинному Е < 0, а при нормальному розподілі Е = 0. Наприклад,
Отже, в даному випадку має місце слабка плосковершинність розподілу.
Закономірність розподілу одиниць сукупності за значеннями варіючої ознаки можна описати певною функцією, яка має назву теоретичної кривої розподілу. Найбільш часто використовується нормальна крива розподілу, а сам розподіл, котрий можна описати цією кривою, має назву нормального розподілу. Він має наступні властивості:
68,3% одиниць сукупності знаходяться в межах Х ± σ;
95,5% — в межах Х ± 2σ;
99,7% — в межах Х ± 3σ.
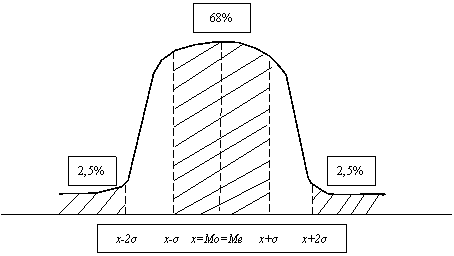
Частоти, які розміщені на кривій нормального розподілу, називаються теоретичними частотами (ft). Відхилення теоретичних та фактичних (емпіричних) частот свідчить про ступінь наближення до нормального розподілу.
Теоретичні частоти знаходяться за формулою:
де і - величина інтервалу;
σ - середнє квадратичне відхилення;
уt - ординати кривої нормального розподілу (знаходяться за спеціальними таблицями):
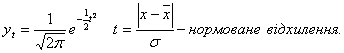
Для об’єктивного судження про відповідність емпіричного розподілу кривій нормального розподілу використовуються спеціальні критерії відповідності (Пірсона, Колмогорова, Ястремського та ін.).
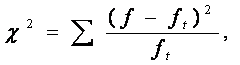
Критерій Пірсона χ2 визначається за формулою:
де f — емпіричні частоти;
ft — теоретичні частоти.
Значення χ2 табульовані для числа ступенів волі k = m–3. У тому випадку, коли χ2 < χ2таб, розподіл можна вважати наближено нормальним, а при χ2 > χ2таб — навпаки, розподіл не можна вважати наближено нормальним.
Отже, χ2 = 6,336. При числі ступенів волі k = 7–3=4 та рівні ймовірності 0,95 χ2таб = 9,5. Оскільки χ2 < χ2таб, розподіл можна вважати наближено нормальним.
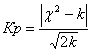
Величини χ2 та k використовуються також для розрахунку критерію сполучення Романовського:
Якщо величина Кр менше 3, відмінності між емпіричними та теоретичними частотами можна вважати несуттєвими, а розподіл — наближено нормальним.
У статистичному аналізі часто використовують критерій сполучення Колмогорова (λ):
де |Dmax| — максимальна різниця нагромаджених емпіричних та теоретичних частот.
Із спеціальних таблиць ймовірностей для λ знаходять величину р(λ). Якщо це значення близьке до нуля — розподіл не можна вважати наближено нормальним, якщо р(λ) прямує до 1 — розподіл нормальний.
За раніше наведеним прикладом:
| Нагромаджені частоти | fн | 2 | 10 | 45 | 86 | 95 | 99 | 100 |
| fнt | 1,47 | 12,45 | 44,73 | 81,17 | 97,02 | 99,62 | 100 | |
| fн – fнt | |D| | 0,53 | 2,45 | 0,27 | 4,83 | 2,02 | 0,62 | 0 |
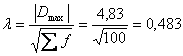
Отже, |Dmax| = 4,83. Тоді
З таблиці при λ = 0,483 р(λ) = 0,97.Розподіл можна вважати нормальним.