8.3. Динамічні міжгалузеві балансові моделі
8.3. Динамічні міжгалузеві балансові моделі
Розглянуті в попередній темі міжгалузеві балансові моделі є статичними, тобто такими, в яких усі залежності стосуються одного й того самого моменту часу. Ці моделі можуть розроблятися лише для окремо взятих періодів, причому в межах таких моделей не встановлюється зв’язок із попередніми чи наступними періодами. Економічна динаміка відображається, таким чином, поза рамками побудованих моделей, що, очевидно, вносить певне спрощення та звужує можливості аналізу.
До таких спрощень насамперед варто віднести те, що у статичних МГБ не аналізуються розподіл, використання та виробнича ефективність інвестицій. Інвестиції винесено зі сфери виробництва до сфери кінцевого використання разом із предметами споживання та невиробничих витрат, тобто включено до кінцевого продукту.
Розглянемо динамічну модель, побудовану як розвиток статичної МГБ, де виробничі капітальні вкладення виокремлюються зі складу кінцевої продукції, досліджується їхня структура і вплив на зростання обсягу виробництва [4, 5]. В основу побудови моделі у вигляді динамічної системи рівнянь покладено математичну залежність між обсягом капітальних вкладень і приростом продукції. Розв’язок системи, як і в разі статичної моделі, приводить до певних рівнів виробництва, але в динамічному варіанті на відміну від статичного ці шукані рівні залежать від обсягів виробництва в попередніх періодах.
Принципову схему квадрантів І і ІІ динамічного міжгалузевого балансу ілюструє табл. 8.2.
Модель містить дві матриці міжгалузевих потоків. Матриця поточних виробничих витрат з елементами xij збігається з відповідною матрицею статичного балансу. Елементи другої матриці ΔФij показують, яку кількість продукції i-ї галузі в поточному періоді j-та галузь спрямовує як виробничі капітальні вкладення у свої основні фонди. Матеріально це виражається у прирості обсягів виробничого устаткування, споруджень, виробничих площ, транспортних засобів тощо в галузях, що споживають відповідну продукцію.
Таблиця 8.2
Принципова схема динамічного балансу
| Галузі, що | Галузі, що споживають | Міжгалузеві потоки | Кінцевий продукт | Валовий продукт | ||||||
| 1 | 2 | … | n | 1 | 2 | … | n | |||
| 1 | x11 | x12 | … | x1n | DФ11 | DФ12 | … | DФ1n | Y1 | X1 |
| 2 | x21 | x22 | … | x2n | DФ21 | DФ22 | … | DФ2n | Y2 | X2 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| n | xn1 | xn2 | … | xnn | DФn1 | DФn2 | … | DФnn | Yn | Xn |
У статичному балансі потоки капіталовкладень не диференціюються за галузями-споживачами і подаються загальною величиною у складі кінцевої продукції Yi кожної i-ї галузі. У динамічній схемі кінцевий продукт Yi містить продукцію i-ї галузі, що йде на особисте та суспільне споживання, нагромадження невиробничої сфери, приріст оборотних фондів, незавершеного будівництва, на експорт тощо. Отже, сума потоків капіталовкладень і кінцевого продукту Yі¢ динамічної моделі дорівнює кінцевій продукції статичного балансу:
![]()
тому рівняння розподілу продукції в динамічному балансі набирає вигляду:
![]()
Міжгалузеві потоки поточних витрат, як і у статичній моделі, можна подати через валову продукцію галузей за допомогою коефіцієнтів прямих матеріальних витрат: xij = aijXj.
На відміну від потоків поточних витрат міжгалузеві потоки капітальних вкладень пов’язані не з усім обсягом випуску продукції, а лише з її приростом, який вони зумовлюють. При цьому в наведеній моделі передбачається, що приріст продукції поточного періоду зумовлюється вкладеннями, зробленими в цьому самому періоді. Якщо поточний період позначити через t, то приріст продукції ΔХj дорівнює різниці абсолютних рівнів виробництва в період t і в попередній щодо нього (t – 1)-й період:
![]()
Вважаючи, що приріст продукції пропорційний до приросту виробничих фондів, дістаємо:
![]()
Розглянемо в останній рівності коефіцієнти пропорційності φij. Оскільки
![]()
то економічний зміст цих коефіцієнтів полягає в тому, що вони показують, скільки продукції i-ї галузі потрібно вкласти в j-ту галузь, щоб збільшити виробничу потужність j-ї галузі на одиницю продукції. Передбачається, що виробничі потужності використовуються цілком і приріст продукції дорівнює приросту потужності. Коефіцієнти φij називаються коефіцієнтами вкладень, або коефіцієнтами прирісної фондомісткості.
За допомогою коефіцієнтів прямих матеріальних витрат і коефіцієнтів вкладень φij динамічну систему рівнянь можна подати в такому вигляді:
![]()
Ця система являє собою систему лінійних різницевих рівнянь
1-го порядку. Її можна звести до звичайної системи лінійних рівнянь, урахувавши, що всі обсяги валової і кінцевої продукції належать деякому періоду t, а приріст валової продукції визначено порівняно з (t – 1)-м періодом:
![]()
Звідси випливають такі співвідношення:
![]()
Нехай нам відомі обсяги валової продукції всіх галузей у попередньому періоді (величини Xj(t–1)) і кінцевий продукт галузей у періоді t. Тоді останні співвідношення являють собою систему n лінійних рівнянь із n невідомими обсягами виробництва t-гo періоду. Отже, розв’язок динамічної системи лінійних рівнянь дає змогу визначити випуск продукції в наступному періоді залежно від рівня, досягнутого в попередньому періоді. Зв’язок між періодами встановлюється через коефіцієнти вкладень φij, що характеризують фондомісткість одиниці приросту продукції.
Переходячи від дискретного аналізу до неперервного, дістаємо:
![]() .
.
Або, переходячи до границі, маємо:
![]()
Остаточно для випадку неперервних змін дістаємо таку систему співвідношень:
![]()
Здобуте співвідношення являє собою систему n лінійних диференціальних рівнянь 1-го порядку зі сталими коефіцієнтами. Для її розв’язання окрім матриць коефіцієнтів прямих матеріальних поточних витрат і коефіцієнтів капітальних витрат (вкладень) необхідно
знати рівні валового випуску в початковий момент часу t = 0 та закон зміни обсягу кінцевого продукту, тобто вид функцій Yі¢(t). На підставі цих даних, розв’язавши відповідну задачу Коші для системи диференціальних рівнянь, теоретично знайдемо обсяги валового випуску для будь-якого моменту часу. Практично ж більш-менш достовірний опис валових і кінцевих обсягів випуску як функцій часу можна дістати лише для порівняно невеликих проміжків часу.
У динамічній моделі особливу роль відіграють коефіцієнти прирісної фондомісткості φij. Вони утворюють квадратну матрицю n-го порядку:

кожен стовпець якої характеризує для відповідної j-ї галузі розмір та структуру фондів, необхідних для збільшення на одиницю її виробничої потужності (випуску продукції). Матриця коефіцієнтів прирісної фондомісткості дає підстави для подальшого економічного аналізу та планування капітальних вкладень.
У розглянутій динамічній моделі МГБ передбачається, що приріст продукції поточного періоду зумовлений капіталовкладеннями, зробленими в цьому самому періоді. Для порівняно коротких періодів це припущення може виявитися нереальним, оскільки існують відомі, іноді доволі значні відставання в часі (так звані часові лаги) між вкладенням засобів у виробничі фонди і приростом випуску продукції. Моделі, що так чи інакше враховують лаги капітальних вкладень, утворюють особливу групу динамічних моделей міжгалузевого балансу. З-поміж теоретичних моделей цього типу варто виокремити насамперед лінійну динамічну МГБ Леонтьева, в якій капітальні вкладення подаються у вигляді так званого інвестиційного блока у формі Леонтьєва. Математичним узагальненням цієї та низки інших динамічних моделей є динамічна модель у матричній формі Неймана, що ґрунтується на математичній теорії рівномірного пропорційного зростання економіки (магістральна теорія).
Модель Неймана. Раніше було розглянуто трисекторну нелінійну динамічну модель економіки. Коли йдеться про розгляд багатьох галузей, доводиться відмовлятися від нелінійності через численні труднощі, що пов’язані з нею. Проте дослідження навіть лінійних динамічних багатогалузевих моделей також становить певні труднощі, хоча й приводить до змістовних економічних висновків.
Модель Неймана є узагальненою моделлю Леонтьєва, оскільки припускає виробництво одного продукту різними способами (у моделі Леонтьєва кожна галузь виробляє один продукт, і жодна інша галузь не може виробляти цей продукт).
У моделі подано n продуктів і m способів їх виробництва, кожний j-й спосіб задається вектором-стовпцем витрат аj і вектором-стовпцем випусків bj у розрахунку на одиницю інтенсивності процесу:

З векторів витрат і випуску утворюються матриці витрат і випуску:
![]()
Коефіцієнти витрат аij, і випуску bij невід’ємні. Природно припустити, що для реалізації будь-якого процесу необхідні витрати хоча б одного продукту, тобто для кожного j знайдеться хоча б одне і, таке що aij > 0, і кожен продукт може бути зроблений хоча б одним способом, тобто для кожного i існує деяке j, таке що bij > 0. З цієї умови випливає, що кожний стовпець матриці А та кожен рядок матриці В повинні мати принаймні один додатний елемент.
Інтенсивність процесів має бути також невід’ємною: ![]() j = 1, …, m.
j = 1, …, m.
Позначимо через xt вектор-стовпець інтенсивності виробництва:
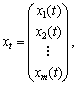
а через рt — вектор-рядок невід’ємних цін: pt = (p1(t), p2(t), …, pn(t)).
Вектор уt = Аxt — це вектор витрат за заданого вектора інтенсивності процесів xt, а вектор zt = Вxt — вектор випусків.
Модель Неймана описує замкнену економіку в тому сенсі, що для виробництва продукції в наступному виробничому циклі (протягом року t витрачається продукція, виготовлена в попередньому виробничому циклі, тобто протягом року (t – 1)):
![]()
при цьому передбачається, що задано початковий вектор запасів Вх0 ≥ 0. Це модель Неймана в натуральній формі.
У рамках моделі Неймана можна ставити і розв’язувати оптимізаційні економічні задачі. Найбільше оптимізаційна задача формулюється так: знайти оптимум лінійної функції стану наприкінці розглянутого періоду:
![]()
