8.7. Оцінка тісноти взаємозв’язку між атрибутивними ознаками
Для аналізу взаємозв'язку між атрибутивними ознаками будуються спеціальні таблиці, що мають назву таблиць співзалежності. В тому випадку, коли утворюються по дві групи за факторною та результативною ознаками, або коли вони є альтернативними, для оцінки тісноти зв'язку визначають коефіцієнти асоціації та контингенції за формулами:
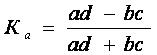і 
.
- сильний зв'язок; 
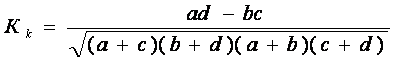- сильний зв'язок.
Для розрахунку названих коефіцієнтів використовують так звані тетрахорічні таблиці, що показують розподіл одиниць за факторною та результативною ознаками.
| Факторна ознака (х) Результативна ознака (у) | х1 | х2 | Разом |
| у1 | 12 а | 198 b | 210 (a+b) |
| у2 | 78 с | 122 d | 200 (c+d) |
| Разом | 90 (а+с) | 320 (b+d) | 410 (n) |
Визначимо коефіцієнти асоціації та контингенції за даними таблиці:
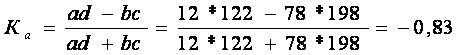
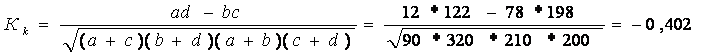
Отже, між Х та Y існує сильний обернений зв'язок.
В тому випадку, коли утворюється більше, ніж дві групи по X та Y, тісноту зв'язку оцінюють з допомогою коефіцієнтів співзалежності:
- Чупрова (при m1 = m2):
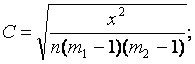
- Крамера (при m1 ≠ m2):
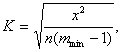де mmin – менше з двох значень.
Значення х2 визначається за формулою:
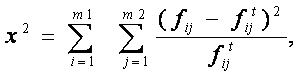
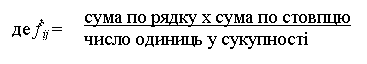
Розглянемо приклад розрахунку коефіцієнта співзалежності:
| xj yi m2=2 m1=3 | х1 | х2 | Разом |
| у1 | 5 3 | 9 11 | 14 |
| у2 | 7 6 | 20 21 | 27 |
| у3 | 1 4 | 16 13 | 17 |
| Разом | 13 | 45 | 58 |
Визначаємо теоретичні частоти:
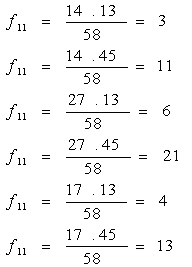
Розраховуємо значення коефіцієнта Крамера, оскільки 
:
К=
Отже, можна зробити висновок, що між досліджуваними показниками існує прямий середній зв'язок.