9.4. Використання сучасної портфельної теорії у портфельному менеджменті. Модель оцінювання капітальних активів (САРМ). Необхідна ставка дохідності. Арбтражна теорія. Оцінювання ефективності управління портфелем цінних паперів. Критерії ефективності

9.4. Використання сучасної портфельної теорії у портфельному менеджменті. Модель оцінювання капітальних активів (САРМ). Необхідна ставка дохідності. Арбтражна теорія. Оцінювання ефективності управління портфелем цінних паперів. Критерії ефективності. Коефіцієнт Трейнора. Коефіцієнт Шарпа

Сучасна портфельна теорія (Modern Portfolio Theory) — теорія фінансових інвестицій, у межах якої за допомогою статистичних методів здійснюють якомога вигідніший розподіл ризику портфеля цінних паперів і оцінювання доходу, складовими елементами її є оцінювання активів (sekuriti valuation); прийняття інвестиційних рішень (asset allocation decision); оптимізація порт­феля (portfolio optimization); оцінювання результатів (performance measurement).

Попри значний рівень абстракції, нехтування доволі важливими, на перший погляд, практичними аспектами (податками й операційними витратами), припущення щодо нескінченної поділь­ності фінансових аспектів, а також абсолютно однакового рівня поінформованості інвесторів стосовно ринкової дохідності й ризикованості фінансових інструментів, розроблення сучасної порт­фельної теорії та подальший розвиток її у САРМ і арбітражній теорії (підходи, розрахунки, коефіцієнти, висновки) мають велике практичне значення. На підставі цих розроблень портфельний інвестор дістає необхідні базові знання стосовно регулювання дохідності й ризику портфеля цінних паперів.

На досконалому (прозорому) ринку цінних паперів фахівець із портфельного інвестування має можливість з’ясування ринкових тенденцій і прогнозування майбутньої динаміки, аналізу інвестиційних властивостей фінансових інструментів, характеристик, що спричинюють зміни в портфелі в разі залучення до його складу окремих активів. Теоретичні аспекти допомагають з’ясувати загальні закономірності ринку цінних паперів і обґрунтовано оперувати ефективними критеріями на практиці.

Стосовно припущень сучасної портфельної теорії зазначимо, що на розвинених фінансових ринках потужні фінансові інститути відзначаються дуже високим рівнем поінформованості, а операційні витрати порівняно з обсягами здійснюваних операцій малі, тому за певних умов ними можна знехтувати.

Модель Марковіца з формування портфеля як комбінації мож­ливих інвестицій можна сформулювати так: слід знайти такі пропорції розподілу інвестицій (коштів) між наявними фінансовими активами, щоб за передбачуваної (прийнятної) очікуваної дохідності ризик портфеля як стандартне відхилення дохідності виявився для інвестора прийнятним (мінімальним). За певного рівня ризику інвестори віддають перевагу більшій дохідності, а за заданого рівня очікуваної дохідності — перевагу меншому ризику.

Марковіц запропонував математичний апарат для пошуку ефективного портфеля, здатного забезпечувати найменший рівень ризику для зазначеного рівня дохідності, або максимізувати очікувану дохідність за прийнятного рівня ризику. Проте модель Марковіца не уможливлює вибір оптимального портфеля, а пропонує набір ефективних портфелів.

Для практичного використання моделі Марковіца необхідно для кожного фінансового активу (акції) визначити очікувану дохідність, її стандартне відхилення і коваріацію між фінансовими активами. Згідно з тлумаченням Марковіца (рис. 9.7), якщо розглянути деякий портфель Z, то він буде неефективним, оскільки портфель F може забезпечити той же рівень очікуваної дохідності за меншого ризику, а портфель U за того ж рівня ризику — більш високу дохідність. Так само можна дійти висновку про неефективність портфеля C. Ефективні портфелі розташовані упродовж лінії HE, яка ілюструє допустиму множину ефективних портфелів. За умови існування багатьох альтернатив інвестування (множини активів) існує і множина ефективних портфелів.

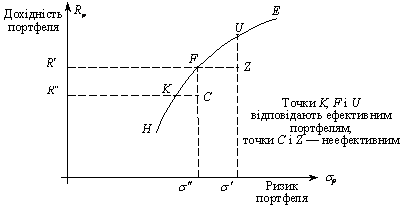
Рис. 9.7. Допустима множина портфелів

Раціональні інвестори завжди прагнуть сформувати ефективний портфель. Яку саме комбінацію фінансових активів обере портфельний інвестор, залежатиме від його намірів і преференцій щодо співвідношення очікуваної дохідності та ризику.

Менше схильний ризикувати інвестор (точка К) згодний втратити у дохідності, а більше здатний на ризик інвестор (точка U) сподіватиметься на вищу дохідність. Утім, спільним для всіх інвесторів, портфелі яких розташовані на лінії НЕ, є прагнення сформувати ефективний портфель.

Вихідна позиція Марковіца ґрунтована на твердженні, що фінансові (портфельні) інвестиції інвестор оцінює за такими параметрами, як очікувана дохідність (приріст доходу на одиницю вкладень) і стандартне відхилення дохідності як міра ризику. Заслуговують на увагу висновки щодо ефекту диверсифікації, котру розглядають як умову зниження ризику інвестування без втрати дохідності шляхом розподілу інвестицій між різними фінансовими інструментами. Чим вищий рівень диверсифікації за меншої кореляції окремих активів, тим ширшими є можливості зменшення ризику.

У загальному вигляді модель Марковіца «дохідність — ризик» — це стандартна модель квадратичного програмування. Втім, техніка створення портфеля за цією моделлю вимагає великої кількості обчислень, а деякі припущення надто ускладнюють отримання вихідної інформації. Прикладне застосування цієї моделі обмежене також складністю інформативного забезпечення розрахунків очікуваної дохідності, стандартного відхилення й коваріації цінних паперів. Так, для моделі Марковіца з N кількістю фінансових активів потрібно розрахувати  коефіцієнтів кореляції. Однак ця обставина в умовах високого рівня комп’­ютеризації не є сьогодні складною проблемою. Значно більшим недоліком і перешкодою застосування моделі «дохідність — ризик» Марковіца є те, що на її підставі пропонується багаточисель­ний набір ефективних портфелів, який ускладнює прийняття конкретного інвестиційного рішення. Але конче важливим є значення розроблень Марковіца для з’ясування підходів і методів обчислення параметрів моделі, засадових підходів і принципів побудови ефективних портфелів, тлумачення поведінки окремих інвесторів, вибору їх рішень щодо розподілу авансованого капіталу серед багатьох альтернативних можливостей спрямування інвестицій.

У межах портфельної теорії особливе прикладне значення має, зокрема, запропонована В. Шарпом (W. Sharpe) модель ув’язу­вання дохідності цінних паперів і систематичного b-ризику (Сapitfl Asset Pricing Model — CАРМ, або модель оцінювання капітальних активів — МОКА).

Заслуговують на увагу головні припущення цієї моделі:

інвестори оцінюють ефективність інвестиційних рішень за двома параметрами — очікуваною (середньою) дохідністю та рів­нем ризику, вимірюваного як b-коефіцієнт;

існує безризикова ставка доходу, однакова як для кредитів, так і для інвестицій;

можливості з безризикованого кредитування й інвестування необмежені, натомість активи нескінченно подільні, тобто існує можливість придбання та продажу активів у будь-якому обсязі;

відсутні податки й операційні витрати, існують необмежені можливості коротких продажів (запозичені активи із зобов’яза­нням повернення);

усі інвестори не схильні до ризику, й інвестують у ризикованіші активи лише заради більших очікуваних доходів (премії за ризик);

усі інвестори однаковою мірою поінформовані стосовно очікуваної дохідності й ризику інвестицій і характеризуються однаковими очікуваннями щодо майбутнього;

фінансові ринки конкурентні, а горизонт прийняття рішень однаковий для всіх інвесторів.

Модель САРМ має такий вигляд:

Ri = Ro + βi ´ (Rm – Ro),

де Ri — очікувана дохідність акцій і-го емітента (необхідна ставка доходу);

Ro — дохідність безризикових цінних паперів;

Rm — середня дохідність ринку цінних паперів;

βi — бета-коефіцієнт як міра систематичного ризику.

Показник надлишкової дохідності ринку (Rm – Ro) має наочну інтерпретацію, бо становить ринкову (середню) премію за ризик за умови вкладання капіталу різною мірою в ризиковані цінні папери (звичайні акції, корпоративні облігації тощо). Аналогічно показник (Ri – Ro) — це премія за ризик у разі вкладання капіталу в цінні папери певного емітента. Модель САРМ означає, що премія за ризик вкладання капіталу в цінні папери конкретного емітента прямо пропорційна ринковій премії за ризик (прямолінійний зв’язок).

Графічне відображення САРМ — лінію ринку капіталу CML можна побудувати, враховуючи, що вона увиразнює компроміс між дохідністю і ризиком для ефективних портфелів. Якщо b-коефіцієнт дорівнює 0, очікувана дохідність дорівнює дохідності безризикових активів (6 %), а якщо 1 — ринковій дохідності 10 %. На підставі зазначених даних отримують дві крапки на графіку (F і M), через які проводять пряму лінію Capital Market Line CML, що демонструє, якою мірою зростання ризику збільшується очікувана дохідність (рис. 9.8).

Очікувана дохідність активу (необхідна ставка доходу), наприклад, дорівнюватиме 11 %, коли β дорівнює 1,25. Якщо збільшити β до 2, дохідність становитиме 14 %.

Нахил лінії CML відбиває рівень несприйняття ризику середнім інвестором. Чим більше несприйняття ризику, тим менший нахил прямої, тим вищі, відповідно, премія за ризик і необхідна ставка доходу.

Рис. 9.8. Лінія ринку капіталу

Важливий підсумок САРМ — побудова лінії ринкової дохідності цінних паперів або лінії ринку фінансового активу (Security Market Line — SML). SML увиразнює те, що в умовах ринкової рівноваги, коли всі інвестори формують найвигідніший для себе портфель, дохідність цінних паперів Rі зумовлена такими чинниками, як безризикова дохідність Rо, дохідність ринкового портфеля Rm, ризик (стандартне відхилення дохідності) ринкового портфеля sm і величина коваріації між дохідністю і-го цінного папера й дохідністю ринкового портфеля sim відповідно до рівняння:

.

Як випливає з наведеного рівняння, відмінності в дохідності цінних паперів зумовлені лише величиною sim, оскільки решта показників рівняння однакові для всіх фінансових активів ринку. Тобто SML графічно інтерпретує залежність очікуваної дохідності цінного папера від коефіцієнта коваріації sim (рис. 9.9). За умови стану рівноваги показники очікуваної дохідності усіх фінансових активів, які обертаються на ринку, повинні розташуватися уздовж прямої SML відповідно до індивідуального значення ризику — коефіцієнта коваріації sim.

Рис. 9.9. Лінія ринку фінансового активу

Проте практики-аналітики ринку цінних паперів для характеристики ризику частіше використовують показник коваріації sim, нормований за величиною дисперсії ринкового портфеля, тобто b-коефіцієнт:

.

Для ринкового портфеля значення чисельника (sim) дорівнює , або

.

На практиці під час побудови лінії ринку фінансового активу на горизонтальній осі графіка зазвичай відкладають значення
b-коефіцієнта.

Розглянемо застосування САРМ на конкретному прикладі.

Інвестиція є прийнятною для інвестора, якщо дохідність фінансового активу становитиме не менше 14 %. Визначимо доцільність альтернативи інвестування коштів в акції компанії Z, яка має β = 1,6, або компанії Q, що має β = 0,9. Безризикова дохідність Ro = 6 %, середня дохідність ринку Rm = 12 %. Очікувана дохідність акцій для компанії Z: RZ = 0,06 + 1,6 ´ (0,12 – 0,06) = 0,156;
для компанії Q: RQ = 0,06 + 0,9 ´ (0,12 – 0,06) = 0,114.

На підставі розрахунків доходимо висновку, що інвестиція доцільна в акції компанії Z. Взаємозв’язок розглянутих показників графічно можна продемонструвати лінією ринку капіталів (рис. 9.10).

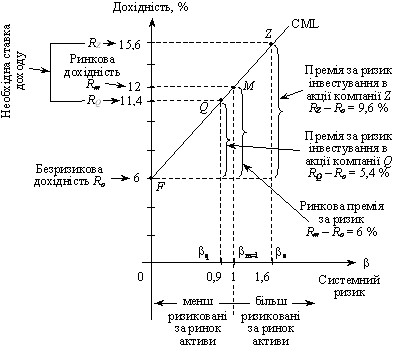
Рис. 9.10. Схема використання CML для розрахунку
очікуваної (необхідної) дохідності акцій

Лінію ринку капіталів можна використати для порівняльного аналізу портфельних інвестицій. Ця лінія (за іншими джерелами — лінія ринку цінних паперів, лінія надійності ринку цінних паперів) дає можливість передбачити необхідну ставку доходу певної акції.

Відбираючи фінансові активи до портфеля, інвестор може визначити, якою має бути дохідність їх за заданого рівня ризику.

Як випливає з САРМ, кожному фінансовому активу відповідає точка на рис. 9.10. Можливі три варіанти розташування цієї точки: на лінії ринку капіталів, вище або нижче цієї лінії. У другому разі актив вважають інвестиційно привабливим, у третьому — не привабливим. Можливі й інші способи використання лінії ринку капіталів.

Якщо безризикова ставка 0,06, середня за (фондовим індексом) дохідність ринку — 0,12, а β-коефіцієнт акції — 1,2, необхідна ставка доходу і-го фінансового активу дорівнює Rі = 0,06 +
+ 1,2 ´ (0,12 – 0,06) = 0,132. Це означає, що акції з ризиком β = 1,2 мають забезпечити дохідність, не меншу за 13,2 %. Якщо дохідність акцій менша, їх треба позбутися, якщо вища — має сенс залучити до портфеля.

Якщо Rі (необхідну ставку доходу) розраховують на майбутній період, дохідність дисконтують за цією ставкою.

Найскладнішим питанням стосовно практичного використання моделі САРМ є визначення показників, а саме безризикової ставки доходу, ринкової дохідності, очікуваної дохідності активів, β-коефіцієнтів як міри системного ризику.

Як безризикову ставку під час практичних досліджень обирають, як правило, дохідність за короткотерміновими (від трьох місяців до року) державним зобов’язанням, облікову ставку (або ставку рефінансування) центрального банку, або розраховану визначеним способом середньозважену ставку за кредитами на міжбанківському ринку (наприклад, ставку LIBOR — London Interbank Offered Rate).

Для розрахунку ринкової дохідності використовують фондові індекси, які вимірюють середньозважений рівень цін за певною групою активів. Серед аналітиків тривають суперечки щодо сутності фондових індексів. Дехто з них взагалі заперечує можливість визначення на їх підставі середніх ринкових показників для САРМ. Утім, практики вже мають достатній позитивний досвід застосування індексів Standart and Poor’s (SP-500) та інших фондових індексів за умови залучення до їх обчислення ринкових цін великої кількості цінних паперів.

Приріст фондового індексу за конкретний період — це середньозважений капітальний дохід за цінними паперами, ціни на які використано під час розрахунку індексу. Проте за багатьма цінними паперами капітальний дохід — це лише одна складова загаль­ного доходу. Так, за акціями також виплачують дивіденди, за облігаціями — відсотки. Крім того, доходи, отримані впродовж певного періоду, можуть бути реінвестовані. За наявності потрібної інформації можна врахувати також середньозважені проміжні доходи за цінними паперами.

Суттєва проблема, пов’язана з практичним використанням індексів, полягає в тому, наскільки індекс адекватний ринковому портфелю (чи в повному обсязі враховано фінансові активи, що обертаються на ринку?).

Загалом проблема під час використання фондових індексів для розрахунку середньоринкової дохідності зводиться до того, що:

1) індекс не враховує дохідність від реінвестування та проміж­них витрат;

2) не повною мірою репрезентує ринковий портфель (наскільки повно він охоплює всі наявні фінансові активи);

3) індекси обчислюють не за ринком (фондовою біржею), а за видами цінних паперів;

4) індекс не враховує закордонних інвестицій.

Водночас іншого підходу для визначення ринкової дохідності, крім використання фондових індексів, поки не знайдено, тому дослідники переймаються переважно лише міркуваннями методів стосовно розрахунку їх.

Загалом середньоринкову дохідність ринкового портфеля цінних паперів Rm можна обчислити за формулою:

Rm = Rk + RD + Rp ,

де Rm — дохідність ринкового портфеля за індексом;

Rk — дохідність від приросту капіталу (ринкових цін);

RD — дохідність від виплати дивідендів і відсотків;

Rp — дохідність від реінвестування коштів.

Під час використання розроблень портфельної теорії найпростішим і найчастіше застосованим на практиці підходом до розрахунку очікуваної дохідності й міри ризику є розрахунок на підставі історичних значень. Головна суперечність такого підходу поля­гає в тому, що мають використовувати майбутні показники (значення ex ante), тоді як наведений метод уможливлює застосування лише оцінок минулих значень (ex post). Справді, подеколи історичні показники дохідності можна розглядати як підґрунтя прогнозування, однак за інших умов зв’язок між попередньою динамікою дохідності та її майбутніми змінами може бути цілком відсутній.

Для прогнозування майбутньої дохідності фінансових активів існує ціла низка підходів. Чим важчий і точніший метод прогнозування, тим більше витрат часу і коштів він потребує від аналітика, тим повнішою має бути вихідна інформація. Саме тому практикам часто доводиться користуватися грубими оцінками (ex post).

Для розрахунку β-коефіцієнта також використовують минулі значення дохідності окремих активів і ринкового портфеля загалом (на підставі індексу). Проте значення дохідності є показниками ex post тож оцінки за розрахунками можуть суттєво відрізнятися від того, що станеться в майбутньому. Але саме цей метод є найпоширенішим завдяки його простоті.

Значення β визначають на підставі пошуку параметрів регресивної моделі «характеристичної» лінії («Characteristic» Line) типу Ri – Rо = αі + βі (Rm – Rо), де Ri — дохідність і-го цінного папера (рис. 9.11), Rо — безризикова ставка доходу, αі — постійна надлиш­кова дохідність активу, Rm — середньоринкова дохідність, βі — тангенс кута нахилу, міра системного ризику. Ця модель визначає залежність між надлишковою дохідністю (премією за ризик) і-го цінного папера (Ri – Rо) і надлишковою дохідністю ринку (Rm – Rо). Значення αі може бути більшим і меншим за 0. Чим вище α, тим привабливіша акція. Якщо α > 0, актив недооцінено, якщо α < 0, актив переоцінено. За американським висловом: «keep your α high and β low» (дотримуйся високого α і низького β). Дисперсія окремих емпіричних значень навколо «характеристичної» лінії не має бути великою. За умови значного розпорошення під час розрахунків слід врахувати додаткові елементи ризику.

Для спрощення розрахунків α і β на практиці застосовується модель типу Ri = αі + βіRm, де Ri — дохідність і-го цінного папера, Rm — дохідність ринку, αі і βі — відповідні параметри.

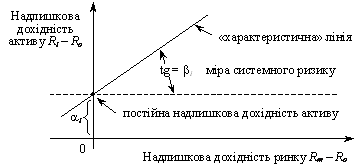
Рис. 9.11. «Характеристична» лінія для визначення β-коефіцієнта

На ринках цінних паперів деяких країн створено спеціальні служби, які визначають β-коефіцієнти акцій і регулярно публікують їх. У США розрахунки β-коефіцієнта здійснюють компанії Merril Lynch та Value Line. Значення β знаходиться в межах від 0,5 до 1,5. У розрахунках зазвичай використовують інформацію про минулі коливання ринкових цін. Деякі фахівці отримують оцінки β на підставі використання спеціальних факторних моделей.

У розрахунках використовують переважно інформацію стосовно щотижневих даних за два роки або щомісячних — за п’ять років. Значення β-коефіцієнта для американських цінних паперів, наприклад, оцінюють на підставі біржового індексу Standart and Poor’s 500 та сукупного індексу Нью-Йоркської фондової біржі. Хоча вважається, що оцінки β як міри ризику для окремих паперів дуже приблизні, вони, за відсутності інших, часто дістають практичне застосування у ринковому аналізі. Утім, ставитися до рекомендацій щодо β слід критично.

Практики нерідко застосовують коригування β. Найпростіший метод коригування ґрунтований на твердженні, що за умов відсут­ності будь-якої інформації можна припустити, що β дорівнює одиниці. Відтак, якщо ринковий аналітик отримав значення історичної β, її справжнє значення перебуває в інтервалі між одиницею та розрахунковим значенням. Скориговану β (βа) отримують на підставі формули:

βа = γ ´ βh + (1 – γ),

де βh — історичне значення β;

γ — умовно прийнятий коефіцієнт, який зазвичай перевищує 0,5 (але менше за 1).

Скориговану βа (adjusted beta) для кожної акції ринкові аналітики умовно часто розглядають як суму середньоринкової β вагою 34 % та історичної β вагою 66 %. У загальному вигляді скоригована β дорівнює:

βа = 0,34 + 0,66 ´ βh ,

де βа і βh — скоригована та історична β відповідно.

Із наведеного рівняння бачимо, що згідно з поправкою значення історичної β коригується в бік наближення до 1.

Існують й інші підходи до уточнення β залежно від минулої інформації щодо запозиченого капіталу, галузевої належності компанії, дивідендної дохідності тощо.

На практиці з огляду на особливості обчислення β, а також спрощення моделі, САРМ можна розглядати лише як орієнтовну. Однак її застосування дає змогу значно обмежити кількість вхідних параметрів. Наприклад, важливо, що за умови залучення
100 різних видів фінансових активів для моделі Марковіца слід обчислити 4950 параметрів, для моделі Шарпа — лише 201.

Модель Шарпа, як і модель Марковіца, застосовують лише для умов стабільного і прогнозованого фондового ринку. У країнах з фондовими ринками у фазі становлення, до яких належить Україна, практичне використання цих моделей ускладнено. За нестабільного ринку достатньо ефективно впроваджують модель «Квази-Шарп» [15]. Її доцільно використовувати за обмеженої кількості фінансових активів окремого ринкового сегмента з однієї або кількох галузей.

На думку фахівців, модель «Квази-Шарп» уможливлює підтримування оптимальної структури наявного портфеля. Суттєвий недолік цієї моделі в тому, що вона орієнтована на ізольоване розглядання певного сегмента ринку без врахування загальних тенденцій і зрушень.

Утім, модель Шарпа теж має недоліки, зокрема, не враховує мінливість безризикової ставки доходу.

Більш узагальненою порівняно з САРМ є арбітражна теорія оцінювання капітальних активів (АТО). Однофакторна модель АТО дуже подібна до САРМ, проте важливо, що АТО враховує вплив на дохідність фінансових активів не лише ринкового ризику, а й інших чинників (це багатофакторна модель).

Для оцінювання інвестиційних рішень портфельному аналітикові треба з’ясувати, наскільки доцільними будуть ці рішення, чи достатньою мірою обрана стратегія відповідає інвестиційним цілям. Оцінювання управління портфелем уможливлює правильний вибір з-поміж альтернативних можливостей розміщення кош­тів у фінансових інструментах.

Головним критерієм ефективності управління портфелем цінних паперів є його дохідність — R за певний проміжок часу. Дохідність за певний період R принципово складається з капіталізованої дохідності, пов’язаної зі змінами курсової ціни, і дивідендної (відсоткової) дохідності.

Дохідність портфеля можна визначити як приріст вартості на одиницю вкладень і розрахувати на підставі формули:

,

де Vn — вихідна ринкова вартість портфеля цінних паперів (на початок періоду);

Vk — ринкова вартість портфеля цінних паперів на кінець періоду.

Одначе наведена формула не враховує розміру вкладень у пев­ний актив із відповідною дохідністю. Тому додатково аналізують показник середньозваженої дохідності портфеля цінних паперів:

,

де R — середньозважена дохідність портфеля;

Ri — дохідність і-го фінансового інструменту;

Vi — вкладення в і-й фінансовий інструмент;

V — загальна вартість портфеля.

Як показник ефективності управління портфелем цінних паперів використовують також його середню дохідність за певний історичний період. Середня дохідність портфеля R визначається як

,

де Rt — дохідність у t-му минулому періоді,

Т — кількість розглядуваних минулих періодів.

Проте показник середньої дохідності не враховує ризику.

Висока дохідність портфеля може зумовлюватися високим ризиком інвестиційних рішень або впливом випадкових чинників, і не свідчити про ефективність управління. Для адекватного оцінювання ефективності управління потрібне додаткове коригування на ризикованість вкладень. Відтак оцінку ефективності управління портфелем цінних паперів можна давати на підставі порівняльного аналізу з урахуванням ризикованості реалізованих інвестиційних рішень та оцінки достатньої тривалої стабільності рівня дохідності інвестицій.

Оскільки в минулому не були відомі підходи, які одночасно поєднували дохідність і ризик, портфельні аналітики розглядали зазначені чинники ефективності ізольовано, групуючи портфелі спочатку на підставі ознаки мінливості доходів у класи з однаковим рівнем ризику, а потім й у межах кожного класу порівнювали дохідність окремих портфелів. Сьогодні відомо три основні складові оцінювання ефективності портфеля цінних паперів, здат­ні об’єднати дохідність і ризик — безпосередньо дохідність, стан­дартне відхилення і b-коефіцієнт як міру ризику.

Проте оцінювання ефективності управління портфелем не можна здійснювати ізольовано (абсолютно), без порівняння з іншими реальними портфелями або ринковим (індексним) портфелем.

Дж. Л. Трейнор (J. L. Traynor) уперше запропонував критерій (коефіцієнт), який врахував одночасно дохідність і ризик. За еталон для оцінювання ефективності конкретного портфеля цінних паперів використано показник надлишкової дохідності ринкового портфеля, розрахований на підставі реального фондового індексу і віднесений до рівня ринкового ризику b.

Критерій Трейнора обчислюють за певний період часу, він являє собою відношення надлишкової дохідності (премії за ризик) портфеля до показника (міри) системного ризику β.

Для i-го портфеля цінних паперів він становить (Ті):

,

де Rі — середньорічна дохідність і-го портфеля за певний період;

Rо — середньорічна безризикова ставка доходу за цей же період;

bі — історичний b-коефіцієнт і-го портфеля за цей період [10].

Для ринкового портфеля критерій Трейнора (Тm) становить:

,

де Rm — середньорічна ринкова дохідність за певний період;

Rо — середньорічна безризикова ставка доходу;

βm — коефіцієнт b як міра системного ризику ринкового портфеля (βm ринку = 1,0).

Вище значення критерію Ті свідчить про досконаліший склад портфеля інвестора, незалежно від його ставлення до ризику. Зазначимо, що у критерії Трейнора змінна ризику визначає лише ринковий (системний) ризик. Системний (ринковий) ризик є конче важливим, оскільки залишковий ризик можна звести до мінімуму (елімінувати) за рахунок широкої диверсифікації портфель­них інвестицій. Критерій Трейнора дає змогу зіставляти різні портфелі на підставі відносного показника надлишкового доходу за портфелем на одиницю вимірювання системного ризику.

Припустімо, що за останні n років середньорічна дохідність сукупного ринкового (індексного) портфеля становила 16 %, тобто Rm = 16, а безризикова дохідність Rо — 8 %. За портфелем цінних паперів фірми «Делмі» середня дохідність за той самий проміжок часу становила 17 %, фірми «Лайн» — 0,32 %, фірми «Грета» — 14 %, показники системного ризику β відповідно β1 = 0,89, β2 = 1,08 і β3 = 1,2.

На підставі цієї інформації можна обчислити критерій Трейнора для ринкового портфеля (Тm) і кожного (і-го) портфеля зазначених фірм:

;

;

;

.

Найвище значення критерію Трейнора Т2 притаманне портфелю цінних паперів фірми «Лайн». Цей портфель забезпечив найвищу дохідність на одиницю ризику й згідно з розрахунками може вважатися найефективнішим.

У. Шарп запропонував інший критерій (коефіцієнт), подібний до критерію Трейнора, але який враховує загальний ризик портфеля, визначений як стандартне відхилення, а не тільки системний b-ризик. Розрахувати за певний період ризик як стандартне відхилення за звичайною формулою вибіркового стандартного відхилення портфеля (історичного стандартного відхилення) відносно нескладно, хоча й потребує певних зусиль.

У загальному вигляді для і-го портфеля критерій Шарпа (S) за певний період визначають так:

,

де Rі — середньорічна дохідність і-го портфеля за певний період;

Rо — безризикова дохідність;

sі — історичне значення стандартного відхилення і-го портфеля.

Числівник цього рівняння визначає надлишкову дохідність (премію за ризик), знаменник — загальний ризик, тобто критерій Шарпа визначає премію за ризик на одиницю вимірювання загаль­ного ризику.

Коефіцієнт Шарпа вважається найпростішим серед показників оцінювання ефективності управління портфелем. У загальному розумінні він характеризує для портфеля міру стабільності (стійкості) перевищення безризикової дохідності (надлишкової дохідності).

Припустімо, що середньорічна дохідність ринку Rm упродовж n років дорівнює 16 %, а безризикова дохідність Rо — 8 %. Стандартне відхилення як показник ризику (s) приблизно 21,2 залишається незмінним на ринку акцій упродовж багатьох років, тому саме це значення найчастіше використовують у різних обчисленнях у разі поточного оцінювання і на майбутнє. Додатково розглядаються дані стосовно портфелів цінних паперів фірми «Е», «І» і «K», які мали в аналізованому періоді середньорічну дохідність відповідно 17, 32 і 13 % і стандартне відхилення як міру ризику відповідно 0,13, 0,19 і 0,13.

На підставі наведених даних обчислюємо коефіцієнт Шарпа: для ринку

;

для портфелів цінних паперів зазначених фірм

;

;

.

Аналізуючи ці дані, можна дійти висновку, що найефективніший портфель у фірми «І». Найнижчий рівень премії за ризик на одиницю вимірювання ризику має портфель фірми «K». Проте всі розглянуті портфелі ефективніші за ринок.

Розглянемо цікавий приклад [10] оцінювання ефективності портфелів цінних паперів двох фірм із такими інвестиційними характеристиками за певний період, які наведено в табл. 9.1.

Таблиця 9.1

	Середньорічна дохідність	Стандартне відхилення дохідності	β-коефіцієнт
Портфель 1	0,25	0,10	0,95
Портфель 2	0,30	0,20	1,05

Якщо середня безризикова ставка доходу за цей період умовно становила 0,10, критерії Трейнора, визначені з використанням b-коефіцієнта портфеля, розрахованого відносно ринкового індексу для цих портфелів, дорівнюють:

Критерії Шарпа:

Аналізуючи одержані результати, дійдемо висновку, що згідно з критерієм Трейнора, ефективнішим можна вважати другий портфель, але, згідно з критерієм Шарпа, ефективнішим виглядає перший портфель. Як свідчить практика, трапляються поодинокі випадки, коли коефіцієнти Трейнора і Шарпа дають протилежні оцінки ефективності портфелів. У наведеному прикладі це обумовлено тим, що вартість першого портфеля набагато менш мінлива від вартості ринкового (індексного) портфеля.

Для повністю врізноманітненого портфеля (портфеля, позбавленого будь-якого диверсифікованого несистемного ризику) кри­терій Трейнора і критерій Шарпа збігаються, оскільки цілковита дисперсія повністю врізноманітненого портфеля є водночас системною дисперсією. Зазначені критерії доповнюють одне одного, тому їх слід використовувати в аналізі ефективності управління портфелями разом.

Теорія пропонує й інші, складніші підходи до оцінювання ефективності управління портфелем цінних паперів, які на практиці застосовують рідко. Це насамперед критерій Дженсена і так звана техніка декомпозиції надлишкового доходу Фейма.