1.3. Застосування методу екстраполяції засобом математичної функції для прогнозування міжнародних туристичних прибуттів
У статистиці під туризмом розуміють одну з форм міграції населення, не пов’язану зі зміною місцепроживання або роботи. Необхідність його дефініції виникла у першій половині XX ст. і була зумовлена збільшенням туристських потоків, зростаючим економічним значенням туризму і, як наслідок, спробами статистичного обліку подорожуючих осіб.
Одне з перших визначень туриста належало Комітету експертів з питань статистики Ліги Націй (1937 р.). Воно одержало міжнародне визнання і в основному дійшло до наших днів з деякими пізнішими поправками. Сьогодні у міжнародній практиці широко використовується визначення, вироблене на Міжнародній конференції зі статистики подорожей і туризму (Оттава, 1991 р.) і схвалене ВТО і Статистичною комісією ООН. Відповідно до нього, турист — це відвідувач, тобто «особа, яка подорожує і здійснює перебування в місцях, що знаходяться за межами його звичного середовища, на термін не більше 12 місяців з будь-якою метою, окрім заняття діяльністю, що оплачується з джерел у місцях, які відвідуються».
Запропонована дефініція дозволила чіткіше окреслити ту частину подорожуючих осіб, яка виступає об'єктом статистичних досліджень у туризмі. У підсумкових документах Оттавської конференції і технічних посібниках ВТО турист визначається як відвідувач. Це поняття рекомендується використовувати як основне в статистиці туризму. Воно поширюється разом з туристами і на одноденних відвідувачів. Очевидно з цієї причини в Оттавському визначенні відсутня мінімальна тривалість перебування за межами звичайного середовища (24 години), яка присутня у багатьох національних туристських законодавствах.
Статистика міжнародного туризму складається з двох основних розділів: статистика туристських потоків і статистика туристських доходів і витрат. Для кожного з них ВТО розробила перелік основних показників, інформативних і таких, що відносно легко вимірюються. Найважливішим показником туристських потоків є кількість прибуттів (arrivals).
Під кількістю прибуттів розуміється число зареєстрованих відвідувачів тієї чи іншої країни, які не є її резидентами, за певний проміжок часу, зазвичай за рік. Усіх їх можна поділити на одноденних відвідувачів і туристів (відвідувачів, що перебувають у країні призначення понад одну ніч). Їх вимірюють за допомогою показників, які наведені у табл. 1.
Табл. 1.
| Об’єкт | Показник | Місце | Коментарі |
| Відвідувач | Прибуття | На кордоні |
|
|
Турист |
Прибуття | На кордоні | |
| У готелях і подібних закладах | Не враховуються поселення у приватному секторі. Враховується кожне нове поселення в іншому закладі розміщення. | ||
| У колективних туристичних закладах |
Відповідно до табл. 1 усі показники вимірювання прибуттів у міжнародному туризмі поділяються на такі категорії:
TF – прибуття міжнародних туристів, що обліковуються на кордоні (за винятком одноденних відвідувачів);
VF – прибуття міжнародних відвідувачів, що обліковуються на кордоні (враховуючи туристів та одноденних відвідувачів);
TCE – прибуття міжнародних туристів, що обраховуються в колективних туристичних закладах;
THS – прибуття міжнародних туристів, що обліковуються в готелях і подібних закладах.
При вимірюванні прибуттів у міжнародному туризмі надається перевага облікованою на кордоні. Однак не всі країни можуть збирати такі дані. Тоді замість цих показників можуть бути використані інші.
Оскільки турист може за рік здійснити декілька подорожей або протягом однієї поїздки відвідати декілька країн, фактичне число туристів менше за кількість прибуттів.
Статистика прибуттів містить кількісний опис туристських потоків у світі. У 2005 році число міжнародних туристських прибуттів перевищило 800 млн. Не зважаючи на короткочасні коливання і спади в окремі роки, у розвитку туризму простежується стійка тенденція до зростання.
Аналіз динаміки прибуттів у минулому з метою виявлення певних тенденцій у зміні даних статистичного ряду дозволяє екстраполювати ці тенденції на майбутній період. На підставі цього можна робити перспективні розрахунки вищевказаних показників міжнародного туризму.
Найбільш корисним для прогнозування є екстраполяція засобом математичної функції. Математична функція є строгим інструментом, який підлягає статистичному аналізу та перевірці. Використання математичної функції для прогнозування базується на припущенні, що показники міжнародного туризму у минулому змінювались згідно з деякою тенденцією, відповідно до якої вони є функцією часу. У такий спосіб отримуємо рівняння
ARt+ye = f (YE),
де: ARt+ye – кількість міжнародних туристичних прибуттів у світі в рік t+YE; t – базовий рік; YE – різниця між роком t+YE, на який робляться розрахунки, та базовим t роком.
Хоча перші статистичні дані Всесвітня туристична організація (ВТО) дає на 1950р., базовим роком t у цьому випадку обраний 1945р. Це пов’язано з тим, що у цей час закінчується Друга світова війна, під час якої майже повністю були згорнуті міжнародні туристичні потоки. Отож можна припустити, що при YE = 0 кількість міжнародних туристичних прибуттів AR також наближується до нуля. Таке припущення важливе у випадку побудови квадратичної функції. Воно дозволяє уникнути того, що у період, близький до 1950р., парабола досягне свого екстремуму та з подальшим наближенням до 1945р. AR почне зростати.
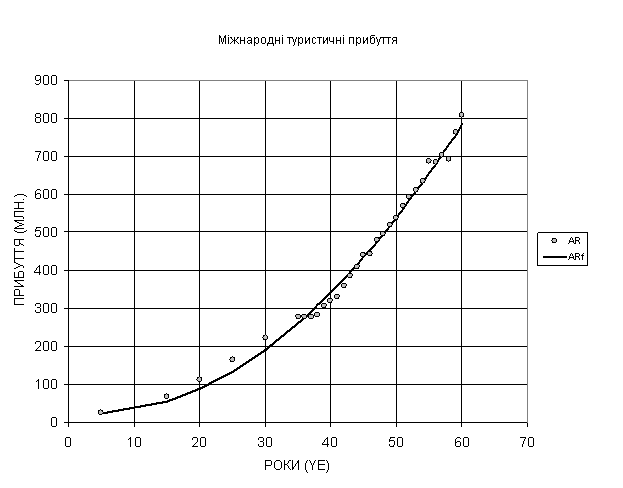
Побудова математичної функції має на меті апроксимацію зв’язку між емпіричними даними x та y, що зазначені у таблиці 2. При цьому треба обрати такий тип функції, який би дозволив отримати результати, максимально наближені до статистичного ряду. Для вибору типу формули будується графік зв’язку між емпіричними даними x та y в прямокутних координатах (рис 1).
Зіставлення положення точок на графіку з кривими відомих рівнянь може вказати на тип функції. У даному випадку найбільше підійшли квадратична, степенева та показова функції. Для більш точного підбору типу рівняння криві треба спрямити через лінеарізацію функцій. Для цього, у тому числі використовуються логарифмічні та напілогарифмічні шкали. Найліпше наблизились положення точок до прямої при лінеаризації квадратичної функції. треба, для відображення емпіричного зв’язку рівнянням був обраний квадратний тричлен
y = B0 + B1x + B2x2, (1)
де: B0, B1, B2 – параметри, що необхідно визначити.
Відповідно виводиться рівняння регресії із використанням методу найменших квадратів, суть якого полягає в тім, що для ліпшої кривої сума квадратів відхилень точок від лінії зв’язку має бути мінімальною. Метод найменших квадратів є найточнішим і забезпечує надійні результати.
Для квадратного тричлена, згідно з вищевказаним методом, невідомі параметри B0, B1, B2 визначаються шляхом розв’язання системи трьох нормальних рівнянь:
![]() nB0 + B1∑x + B2∑x2 = ∑y
nB0 + B1∑x + B2∑x2 = ∑y
B0∑x + B1∑x2 + B2∑x3 = ∑xy
B0∑x2 + B1∑x3 + B2∑x4 = ∑x2y
де: n – загальна кількість випадків значень змінних величин x та y; ∑x, ∑y, ∑x2, ∑x3, ∑x4, ∑xy, ∑x2y – суми відповідних значень.
Підставляючи дані з таблиці 2, отримуємо таку систему рівнянь:
![]() 32B0 + B11330 + B262300 = 13488,4
32B0 + B11330 + B262300 = 13488,4
B01330 + B162300 + B23049000 = 658364,3
B062300 + B13049000 + B2153715520 = 33209678,1
Розв’язуючи цю систему рівнянь, отримуємо такі результати:
B0 = 25,29817;
B1 = –1,50725;
B2 = 0,2357.
Підставляючи одержані параметри у квадратний тричлен (1), отримуємо рівняння регресії, яке апроксимує зв’язок між кількістю міжнародних туристичних прибуттів (млн.) та часом
y = 0,2357x2 – 1,507x + 25,298 (2)
Окрім виведення рівняння регресії, необхідно визначити статистичну значимість зв’язку. Для цього за рівнянням (2) розраховується теоретична кількість міжнародних туристичних прибуттів ARf для кожної змінної величини YE. Одержані результати зіставляються з відповідними емпіричними показниками AR як графічно (рис. 1), так й аналітично (табл. 3).
Для розрахованих між теоретичними та емпіричними даними відхилень D необхідно визначити середнє значення, медіану та моду. Мода у цьому випадку визначається для інтервального ряду з кроком 5 млн. прибуттів, а її значення береться як середнє між крайніми числами інтервалу:
Середнє арифметичне значення = –0,78;
Медіана = –2,13;
Мода = –2,5.
Аналіз вищевказаних показників дозволить зробити висновок про те, чи є розподіл відхилень нормальним, тобто чи є результати, отримані за рівнянням регресії (2), статистично значимими.
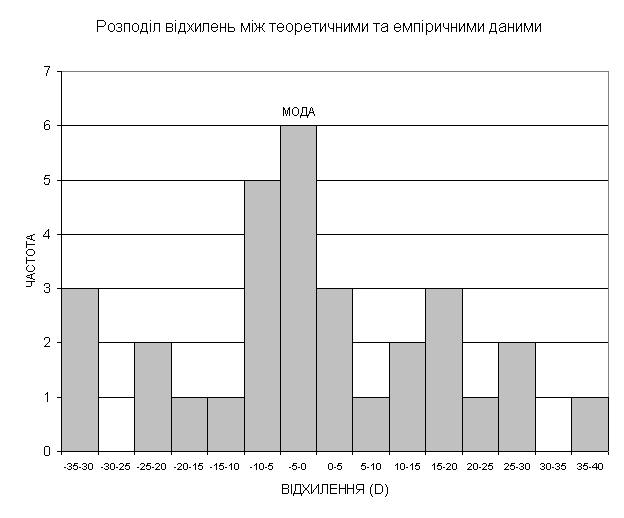
Як показує рисунок 2, відхилення розподілені більш-менш симетрично. Це, а також те, що середнє арифметичне наближається до медіани та обидва ці значення знаходяться у модальному інтервалі, дозволяє стверджувати, що розподіл відхилень близький до нормального.
Аналіз відхилень передбачає також визначення стандартного відхилення σ за формулою
![]() , (3)
, (3)
де: n – загальна кількість випадків значень відхилень D (при невеликій кількості n його значення рекомендується зменшувати на 1, тобто у цьому випадку n = 30); DСР – середнє арифметичне значення відхилень.
Стандартне відхилення σ, розраховане за формулою (3), має значення 17,74 (млн.).
Рис. 1
За нормального розподілу положення варіант у ряду підпорядковується певним закономірностям, які добре вивчені у статистиці. Зазвичай при нормальному розподілі варіаційний ряд не виходить за межі 6σ: 3σ ліворуч від середнього арифметичного та 3σ праворуч. Причому в математиці встановлено, що в межах DСР ± 1σ знаходиться 68,3%; в межах DСР ± 2σ – 95,5%; в межах DСР ± 3σ – 99,7% усіх відхилень.
Розрахунки показують, що:
інтервал DСР ± 1σ має значення від –18,52 до 16,96 млн., у межах яких знаходиться 64,5% усіх відхилень порівняно з 68,3% теоретичними;
інтервал DСР ± 2σ має значення від –36,26 до 34,7 млн., у межах яких знаходиться 96,7% усіх відхилень порівняно з 95,5% теоретичними;
інтервал DСР ± 3σ має значення від –54 до 52,44 млн., у межах яких знаходиться 100% усіх відхилень порівняно з 99,7% теоретичними.
Отож такі дані ще раз доводять, що розподіл відхилень близький до нормального. Це робить результати, отримані за рівнянням регресії (2), статистично значимими.
Рис. 2
Безумовно, число міжнародних туристичних прибуттів є функцією багатьох чинників. Тому для більш точного прогнозування потрібно виводити множинну регресію. Тоді як функція часу надто спрощена, хоча вона й інтегрує у собі дію вищевказаних чинників.
