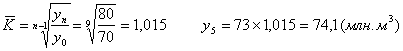10.4. Інтерполяція та екстраполяція в рядах динаміки
Інтерполяцією називають метод знаходження невідомого рівня в межах ряду динаміки. При цьому враховують закономірність зміни показника у часі, що сформувалася у певному інтервалі. Інтерполяцію здійснюють на основі двох суміжних з невідомим рівнів ряду динаміки, або з використанням середніх показників динаміки. Загальні формули для визначення невідомого рівня ряду (yi) мають вигляд:
![]()
![]()
![]()
Приклад розрахунку:
| Дні | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Обсяг добування газу, млн. м2 | 70 | 72 | 71 | 73 | ... | 75 | 74 | 76 | 78 | 80 |
Визначимо невідомий п’ятий рівень ряду динаміки трьома способами:
| 1-й спосіб: |
|
| 2-й спосіб: |
|
| 3-й спосіб: |
|
Екстраполяція — це метод знаходження значення показника за межами відомого ряду динаміки. Цей метод передбачає поширення тенденції ряду у минуле або майбутнє, тому розрізняють ретроспективну та прогнозну екстраполяцію.
Екстраполяція здійснюється на основі середніх показників ряду динаміки або з допомогою рівняння тренду. Прогнозна екстраполяція першим способом виконується за формулами:
![]()
де l — період випередження (l = 1, 2, 3 ...), yn – останній відомий рівень ряду динаміки.
При використання для прогнозу рівняння тренду в одержане рівняння підставляють наступні значення параметру часу (t + l), наприклад, у лінійне рівняння тренду:
![]() .
.
Розглянемо методику використання названих методів прогнозної екстраполяції:
| Дні | Обсяг реалізації, т | t | t2 | y ·t | yt |
| 1 | 300 | -3 | 9 | -900 | 302 |
| 2 | 310 | -2 | 4 | -610 | 306 |
| 3 | 312 | -1 | 1 | -312 | 311 |
| 4 | 315 | 0 | 0 | 0 | 315 |
| 5 | 319 | 1 | 1 | 319 | 320 |
| 6 | 324 | 2 | 4 | 648 | 324 |
| 7 | 326 | 3 | 9 | 978 | 328 |
| Разом | 2206 | 0 | 28 | 123 | 2206 |
Визначимо середні показники ряду динаміки:
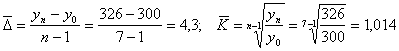
Підрахуємо прогнозні значення показника на наступні три дні двома способами:
|
| Перший спосіб | Другий спосіб |
| l = 1 |
|
|
| l = 2 |
|
|
| l = 3 |
|
|
Лінійне рівняння тренду для наведеного ряду динаміки:
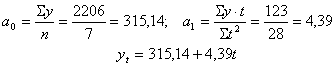
Прогнозній значення показника на основі лінійного рівняння тренду:
| l = 1 |
|
| l = 2 |
|
| l = 3 |
|
При ретроспективній екстраполяції використовують ті ж показники, що й для прогнозування, але формули обчислень змінюються:
![]()
де l — період ретроспективи.
Наприклад, для наведеного ряду динаміки ретроспективні значення становлять:
| l = 1 |
|
| l = 2 |
|
На основі рівняння тренду ряду динаміки одержимо наступні ретроспективні значення:
| l = 1 |
|
| l = 2 |
|
Закономірності динаміки показників формуються під впливом систематичних та випадкових факторів, тому поряд із наявністю основної тенденції (тренду) їм притаманні відхилення від нього, сезонні коливання, структурні зрушення тощо.
Для вимірювання варіації в ряді динаміки використовують абсолютні та відносні показники: розмах варіації, середнє лінійне та середнє квадратичне відхилення, коефіцієнт варіації. Методика визначення цих показників аналогічна тій, що застосовується для індивідуальних даних:
![]()
Розрахункові значення уt одержують на основі середніх показників або рівняння тренду. Коливання фактичних значень ряду динаміки навколо тренду, що проявляється у відхиленні їх від розрахункових, обумовлюється впливом випадкових факторів і вимірюється абсолютними та відносними показниками:
стандартне відхилення: ![]()
коефіцієнт апроксимації: ![]()
Показники S та Va використовують також для підбору оптимального рівняння тренду, для якого ![]() .
.