11.1. Теорія граничної продуктивності та попит на ресурси
На ринку ресурсів виробники як покупці можуть зустрітися з різними моделями. Проаналізуємо ситуацію, коли виробник купує ресурси та продає продукт на конкурентному ринку.
Ресурси задовольняють потреби виробника не безпосередньо, а опосередковано: виробнику немає ніякого смислу купувати працю чи капітал, якщо вони не можуть бути використані ним продуктивно. Тому попит на будь-який ресурс залежить від:
а) попиту та ціни на товар виробника на ринку кінцевих продуктів; б) продуктивності ресурсу при створенні товару. Якщо ресурс є високопродуктивним при виробництві товару, що користується широким попитом на ринку та має досить високу ціну, то попит на такий ресурс буде значним. Разом з тим, якщо ресурс має навіть феноменальну продуктивність, а товар, що виробляється за його допомогою, не має необхідного збуту, то малоймовірно, що якийсь виробник захоче придбати цей ресурс. Унікальність та висока продуктивність ресурсу не є гарантією попиту та високої ціни на нього. Усе зрештою залежить від попиту та ціни на кінцевий продукт. Один з прихильників теорії граничної корисності наголошує: "Не тому дорогі токайські вина, що дорогі токайські виноградники, а навпаки, токайські виноградники дорогі тому, що дороге токайське вино".Таким чином, попит на ресурси є похідним попитом, тобто таким, який залежить від попиту на товари, що виробляються за їх допомогою.
Як ми з'ясували у попередніх темах, у короткотерміновому періоді змінюється лише один фактор, тоді як інші залишаються незмінними. За цих умов діє закон спадної граничної продуктивності змінного фактора, тобто, починаючи з певного моменту, кожна нова додаткова одиниця змінного фактора призводить до меншого приросту продукту, ніж попередня (табл. 11.1). За цією таблицею можна розрахувати граничний продукт змінного фактора у грошовому вираженні (MRP).
Граничний продукт у грошовому вираженні — це приріст загального доходу внаслідок використання кожної додаткової одиниці змінного фактора виробництва. У табл. 11.1 наведено дані про граничний продукт у грошовому вираженні для праці, тоді як капітал залишається незмінним. Аналогічно можна було б розрахувати граничний продукт для капіталу за умови незмінності праці.
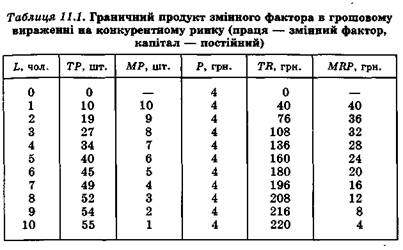
Для вирішення питання про масштаби залучення праці до виробничого процесу виробник, якщо він керується правилом максимізації прибутку, має зіставляти додатковий ефект від залучення нової порції фактора з додатковими витратами, пов'язаними з таким залученням. Величина, на яку зростають сукупні витрати при збільшенні залучених ресурсів на одиницю, називається граничними витратами на ресурси (MRC). Щоб максимізувати прибуток, фірма має використовувати додаткові одиниці будь-якого виду ресурсів доти, поки кожна наступна одиниця дає приріст валового доходу фірми більший, ніж приріст її сукупних витрат. Межею доцільності залучення додаткових ресурсів буде точка, в якій зрівноважуються граничний продукт у грошовому вираженні та граничні витрати на ресурс:
![]()
Оскільки ми припускаємо, що виробник купує ресурси на конкурентному ринку, то ціни на них залишатимуться незмінними і не залежатимуть від кількості залучених ресурсів. Іншими словами, щодо ресурсу праці граничні витрати на ресурс будуть дорівнювати заробітній платі (W). Тоді рівняння {11.1) набуває такого вигляду:
![]()
Якщо, скажімо, заробітна плата становить 20 грн., то для ситуації, що наведена у табл. 11.1, доцільно зупинитися на залученні шістьох працівників, оскільки сьомий коштуватиме виробникові 20 грн., а приріст валового доходу буде лише 16 грн.
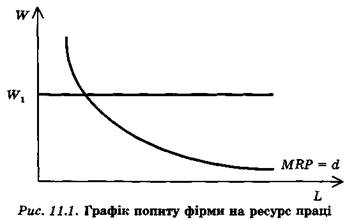
Для моделі конкурентного ринку ресурсів крива попиту на певний ресурс збігатиметься з кривою граничного продукту у грошовому вираженні (рис. 11.1). Його дослідження дає можливість визначити кілька факторів, що впливають на обсяги залучення фактору до виробничої діяльності. Це, по-перше, рівень заробітної плати, який склався на ринку праці. Його зміна перемістить лінію Wl вгору або вниз, що змінить точку її перетину з кривою MRP. По-друге, сама крива МRP може переміститися на графіку під впливом зміни цін на продукт та під впливом зростання продуктивності праці.
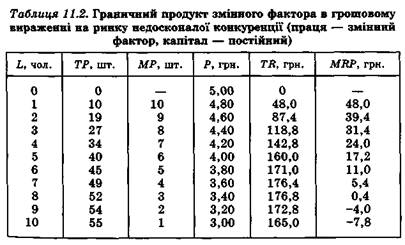
Дещо інакше складається ситуація, коли фірма реалізовує свою продукцію на ринку недосконалої конкуренції. У цьому випадку для збільшення обсягів продажу вона змушена знижувати ціну, а для збіль-
шення ціни відмовлятися від частини обсягу реалізованої продукції. Отже, граничний продукт у грошовій формі зменшуватиметься не тільки під впливом дії закону спадної граничної продуктивності, як це було в умовах досконалої конкуренції, а й під впливом зниження ціни на продукцію (табл. 11.2).
Крива граничного продукту у грошовій формі, як і у попередньому прикладі, є кривою попиту на ресурс праці. Однак для моделей недосконалої конкуренції вона матиме меншу еластичність, ніж на конкурентному ринку. Тому при недосконалій конкуренції виробник менше реагує на зміну заробітної плати при залученні ресурсу праці, ніж виробник в умовах досконалої конкуренції. Це можна продемонструвати, розрахувавши кількість залучених у виробництво працівників при однакових змінах заробітної плати за умов досконалої та недосконалої конкуренції (на основі даних табл. 11.1 та 11.2). Як бачимо з табл. 11.3, обсяги залучених ресурсів при досконалій конкуренції більш активно реагують на зміну заробітної плати.
Як ми з'ясували у розд. З, за інших рівних умов виробник при недосконалій конкуренції виробляє про-

дукції менше, ніж це могло бути на конкурентному ринку. Природно, що для виробництва меншого обсягу продукції виробник залучатиме меншу кількість ресурсів, тому попит на ресурси на ринках недосконалої конкуренції завжди менший, ніж на конкурентних ринках.
Звичайно, криві граничного продукту у грошовому вираженні (криві попиту на відповідні ресурси) для кожної фірми матимуть свій нахил та своє положення на графіку. Відмінності будуть спричинені різним рівнем продуктивності праці та граничного продукту. Щоб визначити ринковий попит на той чи інший ресурс, потрібно підсумувати індивідуальні попити на нього окремих фірм.
