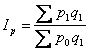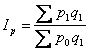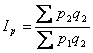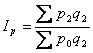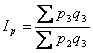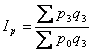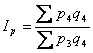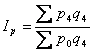11.3. Агрегатний індекс як основна форма загального індексу
Агрегатні індекси відносяться до загальних індексів, які характеризують середню зміну індексованого показника у часі та просторі. В агрегатних індексах у чисельнику та знаменнику знаходяться суми добутків двох взаємопов'язаних показників, один з яких – якісний, а другий – кількісний. Позначаються агрегатні індекси літерою І з підстроковим символом індексованого показника.
В залежності від правил побудови агрегатний індексів розрізняють індексні системи Ласпейреса, Пааше та Фішера. В статистиці України використовується комбінована система агрегатних індексів, яка будується за наступними правилами.
В агрегатних індексах якісних показників індексований показник у чисельнику береться за звітний період, а у знаменнику – за базисний, а співмножник (кількісний показник) у чисельнику і знаменнику фіксується на рівні звітного періоду (метод Пааше). Наприклад,
агрегатний індекс ціни 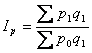 , агрегатний індекс собівартості
, агрегатний індекс собівартості 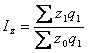 ,
,
агрегатний індекс зарплати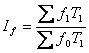 , агрегатний індекс урожайності
, агрегатний індекс урожайності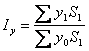 .
.
Таким чином, у чисельнику агрегатного індексу якісного показника знаходиться сума значень об'ємного показника за звітний період, а у знаменнику – розрахункові значення об'ємного показника у звітному періоді при умові збереження якісного показника на базисному рівні.
В агрегатний індексах кількісних показників індексований індексований показник у чисельнику береться за звітний період, а у знаменнику за базисний, а співмножник (якісний показник) у чисельнику і знаменнику фіксується, тобто береться однаковим, на рівні базисного періоду (метод Ласпейреса). Наприклад,
індекс фізичного обсягу 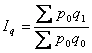 або
або 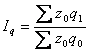 ,
,
індекс чисельності працівників 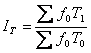 ,
,
індекс посівних площ 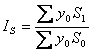 .
.
Отже, у знаменнику агрегатних індексів кількісних показників знаходиться сума значень об'ємного показника за базисний період, а у чисельнику – розрахункові значення об'ємного показника при умові збереження якісного показника на базисному рівні.
В агрегатних індексах об'ємних показників у чисельнику знаходиться сума добутків якісного і кількісного показників за звітний період, а у знаменнику – за базисний, тобто індексуються обидва показники. Наприклад,
індекс товарообороті або вартості продукції 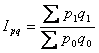 ,
,
індекс витрат на виробництво продукції 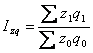 ,
,
індекс фонду заробітної плати 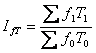 ,
,
індекс валового збору (урожаю) 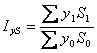 .
.
Отже, в чисельнику цих індексів сумуються значення об'ємного показника за звітний період, а у знаменнику – за базисний.
Між агрегатними індексами показників існує взаємозв'язок: агрегатний індекс об'ємного показника дорівнює добутку агрегатних індексів якісного та кількісного показників. Наприклад, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Наведемо приклад розрахунку та економічної інтерпретації агрегатних індексів:
| Товар | Ціна, грн | Кількість, шт.. | p0q0 | p0q1 | p1q1 | ||
| І кв. (р0) | ІІ кв.(р1) | І кв. (q0) | ІІ кв.(q1) | ||||
| А | 170 | 210 | 70 | 80 | 11900 | 13600 | 16800 |
| Б | 190 | 280 | 90 | 60 | 17100 | 11400 | 16800 |
| В | 150 | 180 | 40 | 20 | 6000 | 3000 | 3600 |
|
|
|
|
|
| 35000 | 28000 | 37200 |
Загальний агрегатний індекс ціни: 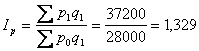
Загальний агрегатний індекс фізичного обсягу: 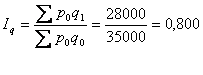
Загальний агрегатний індекс товарообороту: 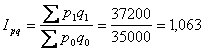
Отже, по трьох товарах ціни в середньому зросли на 32,9%, кількість проданих одиниць (фізичний обсяг) зменшився в середньому на 20%, а товар оборот зріс на 6,3%.
На основі агрегатних індексів можна визначити як загальний приріст об'ємного показника в абсолютному виразі, так і прирости за рахунок зміни якісного та кількісного показників. Для цього від чисельника відповідного індексу необхідно відняти знаменник. Наприклад, загальний приріст товарообороту: ![]() , приріст товарообороту за рахунок зміни цін:
, приріст товарообороту за рахунок зміни цін: ![]() , приріст товарообороту за рахунок зміни фізичного обсягу:
, приріст товарообороту за рахунок зміни фізичного обсягу: ![]() .
.
Приклад розрахунків на основі вищенаведених даних: загальний приріст товарообороту: ![]() ; приріст товарообороту за рахунок зміни цін:
; приріст товарообороту за рахунок зміни цін: ![]() ; приріст товарообороту за рахунок зміни фізичного обсягу:
; приріст товарообороту за рахунок зміни фізичного обсягу: ![]()
Агрегатні індекси можна визначати як ланцюгові та базисні. В ланцюгових індексах індексований показник береться за суміжні періоди часу (наступний і попередній), а у базисних – у знаменнику беруться значення індексованого показника за базисний період. Таким чином, перші індекси характеризують середню зміну індексованого показника за одиницю часу (у поточному періоді порівняно з попереднім), а другі – за певний період часу (у поточному періоді порівняно з базисний). Наприклад, ланцюгові та базисі індекси цін розраховуються за формулами:
ланцюгові базисні