11.3. Кібернетична інтерпретація дій з операторами
11.3. Кібернетична інтерпретація дій з операторами
Відповідно до визначених основних дій з операторами розглянемо, як визначаються складні оператори для систем за різних типів з’єднань блоків та підсистем.
Розглянемо ситуацію, коли деякий стан х характеризує загальний вхід двох систем із лінійними операторами Т1 і Т2, а результатом перетворення стану х є два стани виходів відповідних систем у1
і y2, що підсумовуються. Здобуту суму позначимо через у. Таке з’єднання двох систем називається паралельним (рис. 11.2, а).
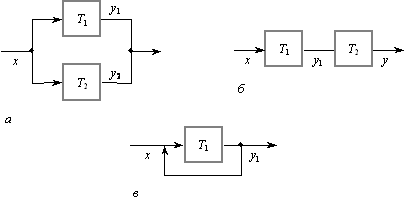
Рис. 11.2. Паралельне (а), послідовне (б)
та зворотне (в) з’єднання систем
У даному випадку операторні формули мають вигляд: y1 = T1x,
у2 = Т2x, звідки
y = y1 + y2= T1x + T2x = (T1 + T2) x.
Результат такої дії можна подати за допомогою одного перетворення у = Тх, де T = T1 + T2.
Звідси випливає таке твердження: оператор перетворення,
в якому дві системи з’єднані паралельно, дорівнює сумі операторів окремих систем.
Це правило можна узагальнити методом індукції на скінчену або злічену кількість паралельно з’єднаних систем.
Розглянемо тепер послідовний зв’язок (послідовне з’єднання) двох систем з лінійними операторами Т1 і Т2 (рис. 11.2, б). У разі послідовного з’єднання стан виходу однієї системи є станом входу іншої. Тоді y1 = T1x та y = Т2у. Підставляючи перше перетворення замість y1 у формулу другого перетворення, дістаємо y = T2T1x — перетворення, рівносильне одному перетворенню y = Тх, оператор якого T = T2T1.
Отже, оператор, що відповідає послідовному з’єднанню двох систем, дорівнює добутку операторів цих систем. Сформульований висновок методом індукції можна також поширити на довільну (скінченну або зліченну) кількість послідовно з’єднаних систем. У техніці послідовне з’єднання низки систем часто називається каскадом.
Оскільки лінійним операторам можна поставити у відповідність «пропускну здатність» (абсолютне значення) відповідних перетворень, то наведені щойно два правила можна сформулювати інакше:
сукупна пропускна здатність систем, з’єднаних паралельно, дорівнює сумі пропускних здатностей цих систем;
сукупна пропускна здатність систем, з’єднаних послідовно, дорівнює добутку пропускних здатностей цих систем.
Розглянемо третій тип з’єднання, який має важливе значення в кібернетичних системах — зворотний зв’язок (рис. 11.2, в). Позначивши перетворення у двох системах, з’єднаних зворотним зв’язком, через у = Т1х і Dх = Т2у, дістанемо відому вже формулу:
![]() .
.
Це співвідношення рівносильне перетворенню y = Tx, де T = T1 / (1 – T1T2). Отже, з’єднання двох систем за допомогою зворотного зв’язку приводить до того, що оператор першої системи Т1 множиться на 1 / (1 – T1T2). Цей останній «співмножник» і є оператором зворотного зв’язку. У разі, коли Т1 і Т2 пропорційні до перетворення, цей оператор рівносильний згадуваному вже коефіцієнту зворотного зв’язку.
Розглянемо два складніших випадки з’єднання систем. У першому випадку припустимо, що існує регульована система, якій відповідає оператор S та з’єднані з нею паралельно дві системи зворотного зв’язку або два регулятори з операторами відповідно R1 і R2 (рис. 11.3, а).
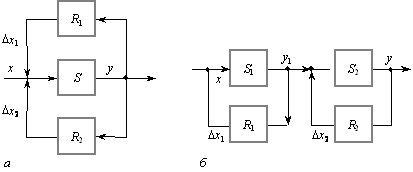
Рис. 11.3. Схема паралельного (а) та послідовного (б)
з’єднання контурів регулювання
Сумарний результат дії цієї системи регулювання можна записати у вигляді одного перетворення у = Тх. Позначимо через D1x і D2x стани виходів відповідно першого та другого регуляторів. Тоді, врахувавши, що D1x = R1y та D2x = R2y, дістанемо:
y = S(x + D1x + D2x ) = S(x + R1y + R2y) = Sx + SR1y + SR2y.
Звідси знаходимо стан виходу:
![]()
Отже, в даному випадку результуючий оператор усієї системи регулювання є T = (1 – S(R1 + R2))–1S. Здобутий результат аналогічний тому, який дістали б, замінивши два паралельно з’єднаних регулятори одним регулятором з оператором R = R1 + R2. Це означає, що замість двох паралельно з’єднаних регуляторів можна поставити один, пропускна здатність якого дорівнює сумі пропускних здатностей окремих регуляторів. Цей висновок можна поширити на довільну скінченну або зліченну кількість регуляторів, з’єднаних паралельно.
У другому випадку припустимо, що система регулювання складається з двох регульованих систем, з’єднаних між собою послідовно, з операторами відповідно S1 і S2, причому кожна з цих систем обладнана регуляторами зворотного зв’язку з операторами відповідно R1 і R2 (рис. 11.3, б).
Стан входу першої системи позначимо через х1, виходу — через y1, стан виходу другої системи — через y.
Сумарний результат роботи такої системи запишемо у вигляді одного перетворення y = Tx. Згідно зі здобутими щойно висновками дістаємо:
![]() і
і ![]() .
.
Тому можемо записати:
![]()
Звідси маємо результуючий оператор розглянутої системи регулювання:
![]() .
.
Наведемо кібернетичну інтерпретацію оператора оберненого перетворення Т–1. Таке перетворення означає, що коли y = Tx, то х = T–1y.
Аналогічно можна довести, що нульове перетворення у =
= (Т – Т)х = 0 — це результат паралельного з’єднання систе-
ми з оператором Т та системи з оператором (–Т), а оператор
(–Т) — результат послідовного з’єднання системи з оператором Т та системи з оператором пропорційного перетворення
(–1).
Розглянуті приклади складних систем можна застосувати до розв’язування конкретних економічних задач. Так, національний дохід y, що дорівнює загальній сумі виплат в економіці, розкладемо на три складові: y = с + I + А, де с — споживання; I — індуковані (чи вторинні) інвестиції, обсяг яких залежить від розміру національного доходу; A — незалежні капіталовкладення, обсяг яких не залежить від національного доходу.
Припустимо далі, що с = c1Y і I = c2Y, причому коефіцієнт споживання 0 < c1 < 1, а коефіцієнт індукованих капіталовкладень 0 < c2 < 1; окрім того, c1 + c2 < l. Тоді дістанемо Y = c1Y +
+ c2Y + A, звідки
![]()
Отже, оператор перетворення у = ТА, що відбувається в роз-
глянутій складній системі, набирає вигляду T = 1 / (1 – (c1 + c2)). Цей вираз — розгорнута форма мультиплікатора Кейнса.
У регульованій системі відбувається тотожне пропорційне перетворення з оператором S = 1. Це означає, що незалежні капіталовкладення перетворюються на дохід, що дорівнює цим капіталовкладенням. З регульованою системою паралельно з’єднано два регулятори з операторами с1 і с2. Комплекс систем такого роду можна замінити системою, що складається з регульованої системи і лише одного регулятора з оператором с1 + с2 = с. Тоді мультиплікатор Кейнса набере колишнього вигляду 1 / 1 – с з тією лише різницею, що тут с є сумою коефіцієнтів споживання та індукованих капіталовкладень.
Комплекс, що складається з двох послідовно з’єднаних регульованих систем з оператором S = 1, кожну з який обладнано регулятором з операторами відповідно с1 і c2, можна інтерпретувати з економічного погляду в такий спосіб.
У першій регульованій системі та відповідному їй регуляторі відбувається перетворення В1 = с1Y1 + A, тобто Y = (1 /1 – с2) A. Нехай ця система позначає країну, що одержує зовнішню позику в розмірі с2Y1, тобто в розмірі, пропорційному до виробленого в ній національному доходу. Цей додатковий фактор (зовнішня позика) зумовлює перетворення, здійснюване у другій регульованій системі та в її регуляторі: Y = Y1 + c2Y, звідки
![]() .
.
Отже, підставляючи вираз для Y1, остаточно дістаємо:
![]() .
.
Таким чином, результуючий оператор розглянутої складної системи є добутком мультиплікаторів обох послідовно з’єднаних систем регулювання.
З проведеного аналізу можна зробити такі висновки. Кібернетична інтерпретація дій з операторами, що відповідають різного роду з’єднанням, дає змогу обчислити результуючий оператор дії цілого комплексу систем. Звідси випливає, що кожна система, оператор якої можна подати у вигляді суми, різниці, добутку або відношення інших операторів, становить комплекс систем, якось з’єднаних між собою.
Системи, в яких відбувається перетворення за допомогою елементарних перетворень або обернених до них операторів, називаються елементарними системами, або елементами.
Тому всі системи являють собою або елемент, або комплекс елементів, певним чином з’єднаних між собою, оскільки кожну алгебраїчну дію з елементарними операторами можна тлумачити як відповідне з’єднання елементів.
