11.5. Індекси середніх величин (змінного складу, постійного складу, структурних зрушень)
У статистичному аналізі часто буває необхідним дослідити зміну у часі або просторі середнього значення якісного показника, наприклад, ціни, собівартості, урожайності, заробітної плати тощо. У цьому випадку середнє значення показника розраховується як середня арифметична зважена або як відношення обсягу ознаки до чисельності сукупності. Слід мати на увазі, що середній рівень будь-якої ознаки формується під впливом двох факторів – варіацією індивідуальних значень та структури сукупності. Наприклад, середній рівень заробітної плати може зростати за рахунок зростання оплати праці кожного працівника і за рахунок збільшення питомої ваги високооплачуваних працівників.
Для вивчення динаміки середнього значення якісного показника використовується система трьох індексів: індекс змінного складу, індекс постійного складу та індекс структурних зрушень.
Індекс змінного складу характеризує зміну у процентах середнього значення якісного показника у звітному періоді порівняно з базисним під впливом двох чинників разом. Цей індекс складається з двох дробів, причому перший дріб містить значення якісного та кількісного показників у звітному періоді, а другий – у базисному, тобто індекс є відношенням звітного середнього значення показника до базисного. Наприклад,
індекс ціни змінного складу 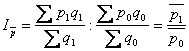 ;
;
індекс собівартості змінного складу 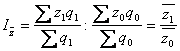 ;
;
індекс заробітної плати змінного складу 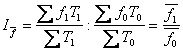 .
.
Індекс постійного складу показує зміну (в %) середнього значення показника під впливом одного фактора – динаміки його індивідуальних значень. У цьому індексі індексується (змінюється) якісний показник, а кількісний фіксується на рівні звітного періоду. Наприклад,
індекс ціни постійного складу: 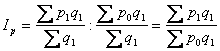 ;
;
індекс собівартості постійного складу: 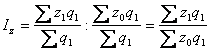 ;
;
індекс зарплати постійного складу: 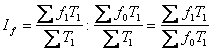 .
.
Індекс структурних зрушень показує, на скільки процентів змінилося середнє значення показника під впливом змін у структурі сукупності. У даному випадку індексується кількісний показник, а якісний фіксується на рівні базисного періоду. Наприклад,
індекс структурних зрушень ціни: 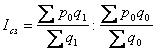 ;
;
індекс структурних зрушень собівартості: 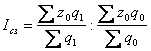 ;
;
індекс структурних зрушень зарплати: 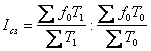 .
.
Між названими трьома індексами існує взаємозв’язок: індекс змінного складу дорівнює добутку індексу постійного складу та індексу структурних зрушень. Отже,
![]() .
.
На основі вказаних індексів можна визначити приріст середнього значення показника в абсолютному виразі загальний та за рахунок окремих факторів — якісного та кількісного (структурного). Наприклад,
приріст середньої ціни (загальний): 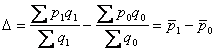 ;
;
приріст середньої ціни за рахунок зміни цін: 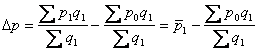 ;
;
приріст середньої ціни за рахунок структурних зрушень:
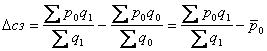 .
.
Наведемо приклад обчислення та економічної інтерпретації індексів середньої собівартості.
| Продукція | Собівартість, грн. | Кількість, тис.шт. | z0q0 | z0q1 | z1q1 | ||
| z0 | z1 | q0 | q1 | ||||
| А | 30 | 37 | 100 | 135 | 3000 | 40550 | 4995 |
| Б | 41 | 40 | 70 | 90 | 2870 | 3690 | 3600 |
| В | 50 | 53 | 140 | 170 | 7000 | 8500 | 9010 |
| Разом | х | х | 310 | 395 | 12870 | 16240 | 17605 |
Індекс собівартості змінного складу:
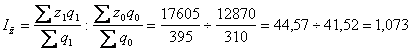 ;
;
Індекс собівартості постійного складу:
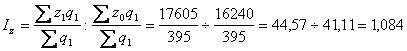 ;
;
Індекс структурних зрушень:
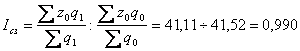 .
.
Таким чином, середня собівартість зросла на 7,3% , в тому числі під впливом зміни індивідуальних значень показника — на 8,4%, а за рахунок структурних зрушень середнє значення зменшилося на 1%.
Приріст середньої собівартості:
загальний ![]() ;
;
за рахунок зміни собівартості: ![]() ;
;
за рахунок структурних зрушень: ![]()
