12.1. Методи прийняття управлінських рішень
12.1. Методи прийняття управлінських рішень
У загальному випадку процес управління економічними системами складається з таких етапів: збору інформації, вибору рішення та здійснення (прийняття) рішення. Ці етапи циклічно повторюються, при цьому на кожному наступному кроці оцінюється якість управління (рис. 12.1).
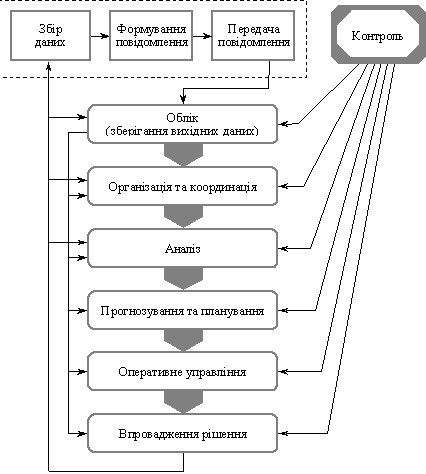
Рис. 12.1. Загальна схема процесу прийняття рішень
Оцінюючи якість управління, за критерій беруть міру досягнення поставленої цілі. Проте можливі й інші критерії, пов’язані з вибором траєкторії руху до досягнення заданої цілі. Критерієм ефективності в такому разі може бути максимальна швидкодія або мінімальні витрати ресурсів для досягнення цілі. Нарешті, критерієм ефективності системи управління може виступати точність, з якою вона веде об’єкт за вибраною траєкторією. Для цього з’ясовують чи не виходять відхилення (які все одно неминучі) за припустимі межі.
СУ на основі обробки та аналізу інформації про об’єкт управління приймає відповідні рішення або подає деякі розпорядження щодо бажаних подальших дій (плани, інструкції, накази, комплекс фізичних керуючих впливів тощо). Прийняття рішення завжди полягає у виборі деякої альтернативи з множини припустимих варіантів. Цей процес вибору, що охоплює і розробку альтернатив, називається процесом прийняття рішень.
І хоча в теорії управління не існує універсальних методів для відшукання оптимального (у деякому сенсі) управління, у її рамках здобуто важливі результати для деяких класів детермінованих і стохастичних систем [2; 6; 10; 13; 14].
Процеси прийняття рішень в економіці базуються передусім на використанні евристичних методів, а останні, у свою чергу, ґрунтуються на застосуванні правил, прийомів, спрощень, що узагальнюють відповідний досвід особи, яка приймає рішення (ОПР). Евристичні міркування — це попередні судження, спрямовані на пошук такого розв’язку задачі, який характеризується більшою або меншою мірою вірогідності.
Окрім цього, здійснювати вибір ефективних рішень допомагає застосування деяких спеціальних методів, таких як системний аналіз, дослідження операцій, мережний аналіз тощо. Ці методи доволі ефективні для розв’язування багатьох управлінських та виробничих проблем.
У процесі прийняття рішення можна виокремити кілька етапів. Основу прийняття рішення становить так званий модельний (уявний) експеримент, що передбачає:
побудову уявної моделі об’єкта управління;
формулювання ідеалізованих умов, що впливають на модель;
довільне комбінування цих умов і їх можливих впливів на модель та оцінювання в думці відповідних ситуацій і можливих наслідків.
Реалізуючи модельний експеримент, перевіряють наявність у робочій пам’яті керуючого органу готового «рецепта» для досягнення поставленої мети (розв’язання відповідної задачі). Якщо такий рецепт існує і ситуація, що склалася, подібна до тієї, в якій цей рецепт вже застосовувався, аналізують можливі наслідки його застосування та виробляють відповідне рішення.
З метою прийняття рішень у детермінованих умовах успішно застосовують математичне моделювання. Адже за допомогою математичних моделей вдається досліджувати реальні системи, відшукуючи їхні характерні особливості й кількісні параметри та формулюючи зрештою задачу прогнозування. Остання полягає у визначенні наслідків, яких можна очікувати в разі реалізації різних варіантів рішень.
У процесі розв’язування задач за допомогою математичного моделювання широко використовують методи прикладної математики, зокрема математичне програмування, методи прогнозування, математичну статистику, теорію ігор тощо, а також комп’ютерну техніку й відповідні пакети прикладних програм.
Зауважимо, що для багатьох економічних задач побудовано достатньо апробовані моделі, які добре зарекомендували себе на практиці. Зокрема, моделі математичного програмування широко використовуються для обґрунтування прийняття рішень стосовно планування асортименту та обсягу виробництва продукції за наявних обмежень на ресурси, планування транспортних перевезень, мінімізації витрат тощо.
З огляду на порівняну простоту розв’язування детермінованих лінійних задач керівники нерідко намагаються зводити реальні задачі до цих умов, не повністю враховуючи або навіть ігноруючи вплив різноманітних об’єктивних чинників. Такий підхід може призвести до прийняття неоптимальних, недостатньо ефективних або й зовсім хибних рішень.
Розв’язуючи задачі в умовах ризику, для оцінювання ймовірностей виникнення тих чи інших ситуацій застосовують методи з таких розділів математики, як теорія ймовірностей та математична статистика. Якщо ймовірності та їхні оцінки визначено з достатньою точністю, то для вироблення рішення можна скористатися математичним моделюванням.
Коли модель об’єкта побудовано в імовірнісних категоріях, задачу управління можна розв’язувати методами математичного програмування (стохастичного, динамічного). Апарат теорії ігор також придатний для розв’язування задач за умов ризику.
Найбільшу складність становить розв’язування задач за умов невизначеності, оскільки для них неможливо зробити достовірний прогноз або оцінити ймовірність впливу різних об’єктивних чинників. До того ж розв’язування таких задач не можна звести до складання математичної моделі, як це робиться для задач, розв’язуваних за детермінованих умов. Як правило, критерієм оцінки якості управління служить міра ризику або рівень втрат, які, за припущенням, може понести ОПР. За умов невизначеності (як і за умов ризику, коли немає достатньої довіри до знайдених оцінок різних варіантів) приймати остаточне рішення може керівник, вибираючи найефективніший, як на нього, варіант.
Велике значення в такому разі мають риси характеру керівника, його досвід, знання, інтуїція. Найбільш обережні прагнуть зазвичай уникати будь-якого ризику, обираючи той варіант рішення, який забезпечує мінімальні втрати за несприятливих обставин, тобто керуються правилом мінімізації максимального збитку, або обережних рішень. Керівник-оптиміст, як правило, намагається вибрати такий варіант рішення, який дає найкращий з усіх кращих результатів, незважаючи на те, що за несприятливих умов він може завдати відчутних втрат (збитків).
Правило обережних рішень застосовують багато керівників, хоча прагнення до максимуму очікуваних результатів іноді буває ефективнішим. Наприклад, керівники підприємств часто вважають за доцільне мати надлишки запасних деталей на складах, щоб не зазнавати ризику виникнення простоїв у виробництві через перебої постачання.
Зауважимо, що нагромадження інформації у процесі розв’язування задачі дає змогу зменшити невизначеність результатів, очікуваних від того чи того рішення. Крім того, реалізація рішення також стає джерелом інформації. Таким чином, невизначеність зменшується завдяки вмінню керівника не тільки передбачити достовірні наслідки від прийняття певного рішення, а й своєчасно скоригувати їх залежно від ступеня досягнення поставленої мети та зміни зовнішніх і внутрішніх умов. Тут постає багатокрокова задача прийняття рішень, в якій реалізується адаптивне управління.
Незважаючи на складність формалізації задач за умов невизначеності, у цьому напрямку здобуто деякі позитивні результати. Вивчено два типи невизначеностей ситуацій: невизначеність стану природи і невизначеність цілеспрямованої протидії. Задачі, що пов’язані з невизначеностями першого і другого типів, досліджують відповідно теорія статистичних рішень та теорія ігор.
Для розв’язування багатокрокових задач за умов невизначеності застосовують динамічне програмування. Прийняття рішень у такому разі являє собою задачу управління, яку у принципі завжди можна формалізувати. Однак під час розробки математичних моделей реальних об’єктів нерідко постають труднощі у тих випадках, коли не всі чинники можна формалізувати й подати кількісними залежностями. Це зумовлюється стохастичністю досліджуваних процесів, а також відсутністю досить повної інформації, необхідної для прийняття обґрунтованих рішень.
Отже, доводиться приймати рішення за умов ризику і невизначеності. Важливе значення має розробка відповідних методів прийняття рішень. У теорії управління розроблено і застосовано на практиці підходи до цієї проблеми. Одним із таких підходів є побудова спрощеної моделі об’єкта, причому спрощення досягається за рахунок нехтування другорядними факторами, звернення до простих загальних правил, пристосування до найближчого горизонту планування, зневажання ризику, тобто заміни невизначеності ситуації певними співвідношеннями.
Іншим підходом до розв’язування задач за умов ризику і невизначеності є застосування евристичних методів, що передбачають широке використання досвіду та інтуїції. Ці методи дають змогу здійснювати пошук рішення тоді, коли навіть не сформульовано задачу і невідомі способи її розв’язування. Раціональне поєднання алгоритмічних та евристичних методів у процесі розв’язування управлінських задач дає найбільший ефект.
Для вибору управлінських рішень за умов неповної інформації розробляються методи, що ґрунтуються на використанні відомої в теорії ймовірностей теореми Баєса. Ці методи дістали назву «баєсівського підходу», що полягає в поєднанні досвіду та інтуїції з нагромадженою інформацією для прийняття рішень. Однак для практичного використання цей підхід розроблений ще недостатньо. Окрім цього, для прийняття рішень у складних умовах ризику, невизначеності та конфліктності застосовується системний підхід (див. наступний підрозділ).
Докладніше з теорією прийняття управлінських рішень ознайомлюють праці [15; 16].
