12.4. Основи функціонування систем криптографічного захисту інформації
Довгий час криптографія була прерогативою держави, а криптографічні алгоритми вважалися військовими технологіями. Поширення інформаційних технологій вимусило до необхідності інтеграціі в них все більш стійких механізмів безпеки, що неможливо без використання надійних криптографічних алгоритмів і це призводить до того, що криптографія втрачає військовий статус. Внаслідок такої ситуаціі, до недавнього часу, з причини браку інформації було важко визначити ступінь надійності криптографічних алгоритмів, та, навіть, знайти іх описи. Це призводило до використання різних примітивних методів криптографічного захисту чи до створення абсолютно ненадійних алгоритмів.
На сьогоднішній день існує величезна кількість криптографічних алгоритмів, що відрізняються як своїми загальними характеристиками, так і принципами, на яких базується їх робота. Не всі вони є однаково надійними - серед них є навіть такі, що оформлені як стандарти та при цьому не забезпечують скільки-небудь реального захисту. Насправді ж, створення надійного криптографічного алгоритму - дуже важка задача. Крім того, надійність є відносна річ - багато з раніше розроблених алгоритмів, які вважалися надійними, тепер або ненадійні, або ця надійність викликає великий сумнів. Тому при розробці криптографічного алгоритму необхідно враховувати тенденціі розвитку комп'ютерної техніки а також інші фактори, що потенційно можуть знизити його стійкість в майбутньому.
Традиційний метод шифрування, що застосовується при організації захисту даних, які пересилаються інформаційно-обчислювальними мережами, базується на факті знання і використання відправником та адресатом повідомлення одного й того ж секретного ключа. Ідея цього, так званого методу криптографії з секретним ключем або симетричної криптографії, полягає в тому, що відправник використовує секретний ключ для того, щоб зашифрувати текст повідомлення, а адресат застосовує цей же ключ для його розшифрування. У випадку компрометації ключа стає можливим несанкціонований доступ до даних, тому для надійного функціонування системи необхідна його періодична заміна. Особливо важливим питанням є спосіб конфіденційного узгодження обома сторонами ключів до використання. Якщо відправник та адресат розділені значними відстанями в просторі, постає питання надійності засобів зв'язку, що ними пересилаються секретні дані: будь-хто, випадково або цілеспрямовано перехопивши секретний ключ, зможе безконтрольно читати, змінювати чи фальсифікувати всі супроводжувані цим ключем повідомлення. Сукупність заходів по створенню (генерації), передачі та зберіганню ключів носить назву адміністрування ключів (АК) і особливо важко забезпечується у відкритих системах з великою кількістю користувачів.
Для вирішення проблем, пов'язаних із АК, в 1976році Уітфілдом Діффі та Мартіном Хелманом була запроваджена концепція системи шифрування з відкритим ключем, яка виключає необхідність відправнику та адресату ділитись секретною інформацією. Кожна зі сторін має свою персональну пару ключів, пов'язаних між собою певною математичною залежністю: відкритий, що публікується і використовується для пересилання повідомлень, і секретний що його використовують для розшифрування прийнятих даних і зберігають у таємниці. Для пересилання конфіденційного повідомлення відправник шифрує його текст за допомогою відкритого ключа адресата, після чого відсилає за місцем призначення, а адресат розшифровує отриману інформацію, застосовуючи свій секретний ключ. Таким чином, будь-хто може прийняти "чуже" повідомлення, але тільки безпосередній адресат може його прочитати.
Генерація ключів в обох системах, як правило, здійснюється за допомогою генераторів псевдовипадкових чисел (ПВЧ), що повинні забезпечувати вихідну послідовність із достатньо довгим циклом повторювання. Це необхідно для виключення можливості появи повторюваних блоків вихідної послідовності, а відтак, її прогнозованості.
Одною з переваг системи шифрування з відкритим ключем є відсутність необхідності покладання на безпеку засобів комунікацій, оскільки між абонентами передаються лише відкриті ключі. Єдина вимога до системи полягає в підборі пари ключів таким чином, щоб секретний ключ неможливо було вирахувати з відкритого. Слід також взяти до уваги забезпечення системою можливості електронного підпису документів, коли адресатові надається додаткова можливість перевірки аутентичності та цілісності одержаного повідомлення, тобто факту, що документ передано в незмінній формі саме від означеного відправника. Недоліком в порівнянні з системою шифрування з секретним ключем є недостатня швидкість функціонування методу.
Слід відзначити, що, попри доцільність окремого застосування кожного із методів при забезпеченні певних типів захисту інформації, в інформаційно-обчислювальних мережах часто застосовується комбінація обох систем для сполучення таких їх позитивних якостей, як швидкість обробки секретних ключів та безпека передачі відкритих. Реалізація такого протоколу "цифрового конверта" передбачає шифрування відкритим ключем секретного, який, в свою чергу, використовується для шифрування тексту повідомлення. Таким чином, обидва підходи при застосуванні в розподілених інформаційних середовищах є взаємодоповнюючими в забезпеченні конфіденційного обміну інформацією.
Алгоритми шифрування можуть бути потоковими чи блочними з довжиною блока 64 біта. Достатня довжина блоку є необхідною умовою для забезпечення високої криптостійкості алгоритму; вважається, що довжина блоку в 64 біта є достатньою.
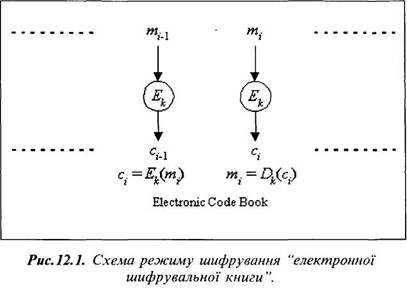
Найбільш простим і очевидним режимом застосування алгоритму шифрування є шифрування блоків відкритого тексту кожного окремо. Такий режим називається ЕСВ (Electronic CodeBook mode - "режим електронної шифрувальної книги"). Але цей режим має багато недоліків і ніколи не повинен використовуватись для надійного шифрування. Одним із цих недоліків є той, що однаковим блокам відкритого тексту відповідають однакові блоки зашифрованого тексту. Схема режиму ЕСВ наведена на рис. 12.1.
Найбільш розповсюджений режим застосування алгоритму шифрування має назву СВС (CipherBlock Chaining - "зчеплення зашифрованих блоків"). В цьому режимі до кожного з блоків відкритого тексту, перед шифруванням, за модулем два додається попередній зашифрований блок. До першого блока відкритого тексту за модулем два додається випадковий блок, вектор ініціалізації, який передається у відкритому вигляді разом із зашифрованим текстом. Схема режиму СВС наведена на рис. 12.2.
Третім режимом застосування алгоритму шифрування є CFB (Cipher FeedBack - "шифрування зі зворотним зв'язком"). Тут кожний блок зашифрованого тексту утворюється шляхом додавання до блока відкритого тексту за модулем два результату шифрування попереднього
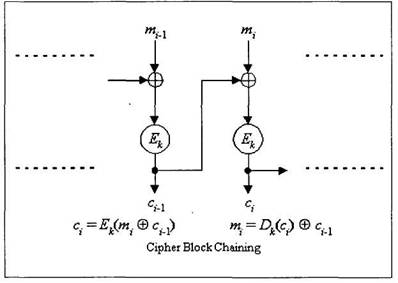
Рис. 12.2. Схема режиму шифрування "Зчеплення зашифрованих
блоків ".
утвореного блока. Вектор ініціалізації використовується в якості нульового зашифрованого блока. Схема режиму CFB наведена на рис. 12.3.
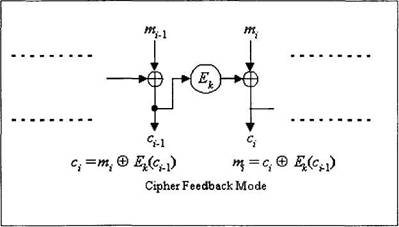
Рис. 12.3. Схема режиму "шифрування зі зворотним зв'язком".
Схема побудови більшості, якщо не всіх алгоритмів шифрування є такою, що основа процесу шифрування уявляє собою послідовність приблизно однакових перетворень, яка повторюється декілька ітерацій. Більша кількість ітерацій може підвищувати криптостійкість, але все в основному залежить від перетворень, які повторюються в ітераціях.
В залежності від кількості ітерацій, характеру перетворень, які виконуються в симетричному алгоритмі шифрування, алгоритм може мати ту чи іншу швидкість роботи. Зрозуміло, не обов'язково, що алгоритм, який має меншу швидкість роботи, є більш криптостійким. Симетричні алгоритми шифрування можуть бути різними за своєю побудовою - існують оригінальні алгоритми, що сильно відрізняються від інших, та існують алгоритми, що мають одну з класичних схем побудови.
Одним із розповсюджених класів алгоритмів шифрування є так звані шифри Фейстеля.
В шифрі Фейстеля відкритий текст, що підлягає шифруванню, розділяється на дві половини. В ітераціях застосовується функція, першим аргументом якої є одна з цих половин, а другим аргументом -один із підключів, які певним чином отримуються з ключа шифрування; генерація підключів із ключа шифрування, як правило, може бути виконана один раз перед власно процесом шифрування. Результат функціі додається за модулем 2 до іншоі половини, після чого ці половини міняються місцями. За таким шаблоном виконуються всі ітераціі, крім останньоі, в якій зміна місцями лівої та правої половин не відбувається (з метою спрощення процесу дешифрування). Загальна схема шифру Фейстеля наведена на рис. 12.4.
Головною властивістю шифру Фейстеля є те, що процеси шифрування та дешифрування є структурно ідентичними. Різниця полягає тільки в тому, що при дешифруванні підключі застосовуються в послідовності, оберненій до тієі, що використовувалась у процесі шифрування.
В багатьох симетричних алгоритмах шифрування використовується поняття S-комірки (S-Box - Substitution Box - комірка підстановки). S-комірка розмірністю уявляє собою таблицю розмірністю, яка задає відображення вхідних бітів на вихідних бітах. S-комірка підставляє (заміщує) вхідне значення на вихідне значення таким чином, що будь-яка зміна у вхідному значенні призводить до хаотичноі зміни у вихідному значенні.
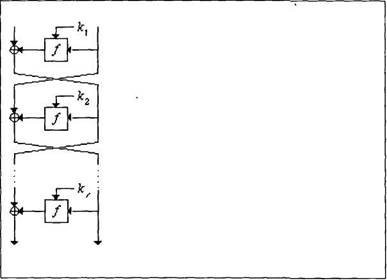
Рис. 12.4. Схема шифру Фейстеля.
Взагалі кажучи, "ідеальний" блочний шифр (із конкретним ключем) може бути представлений як S-комірка, кількість вхідних і вихідних бітів якоі дорівнює довжині блока. Але оскільки при прийнятній довжині блока безпосередня практична побудова такої S-комірки неможлива, в сучасних блочних алгоритмах шифрування фактично використовуються різноманітні прийоми для імітації цієї комірки. При цьому, іноді в алгоритмі шифрування можуть навіть взагалі не застосовуватись S-комірки.
Розмірність і зміст S-комірок, які використовуються в алгоритмі, мають дуже високий вплив на його криптостійкість, в тому числі на його стійкість до лінійних і диференціальних атак. Зрозуміло, що S-комірка заданої розмірності може бути представлена як набір із булевих функцій, кожна з яких має задану кількість аргументів.
Іншою характеристикою S-комірки, що також визначає її надійність, є так звана таблиця розподілу різниць. Перед тим, як дати означення таблиці розподілу різниць, визначимо декілька термінів. При додаванні двох двійкових значень за модулем 2, якщо біти цих значень, що знаходяться на однакових позиціях, є однаковими, то відповідний біт результату приймає значення 0, а якщо різними, то значення 1. Вхідною різницею S-комірки будемо називати результат додавання за модулем 2 двох вхідних значень цієї S-комірки. Відповідно, вихідною різницею S-комірки будемо називати результат додавання за модулем 2 двох вихідних значень цієї S-комірки.'
Нехай X - вхідна різниця, Y - вихідна різниця. Тоді якщо для деякої S-комірки існує пара вхідних значень із різницею X, і існує пара відповідних їм вихідних значень із різницею Y, то будемо казати, що для даноі S-комірки X може викликати Y. Якщо ж для заданої S-комірки та значень X і Y такої пари не існує, то будемо казати, що для даноі S-комірки Х не може викликати Y.
Таблиця розподілу різниць S-комірки має розмірність. її рядки відповідають всім можливим вхідним різницям, а стовпчики - всім можливим вихідним різницям. Елементом таблиці, що відповідає вхідній різниці X і вихідній різниці Y, є кількість пар вхідних значень із різницею X, яким відповідають пари вихідних значень із різницею Y. Таким чином, якщо X викликає Y, то елементом таблиці є число більше 0, а якщо Xне викликає Y, то елементом таблиці є 0.
Будемо казати, що для певноі S-комірки Х може викликати Y із ймовірністю Р, якщо Р є відношення кількості пар вхідних значень із різницею X до кількості пар відповідних вихідних значень із різницею Y. Важливість таблиці розподілу різниць полягає в тому, що вона дозволяє знайти ймовірні пари вхідних і вихідних значень по вхідним і вихідним різницям.
• Отже, знаючи лише різницю між двома вхідними значеннями та ' різницю між двома вихідними значеннями S-комірки, можна з певною ймовірністю визначити, які ці вхідні та вихідні значення.
Таблиця розподілу різниць, яка відповідає надійній S-комірці, повинна містити елементи, що не перевищують 2. Число 2 відповідає деякій парі значень (А,В) і двоістій парі (В,А).
До недавнього часу найбільш широко використовуваним алгоритмом шифрування був DES (DataEncryption Standard - Стандарт Шифрування Даних). Алгоритм розроблений у 1977 році Агентством Національної Безпеки США на основі алгоритму, створеного фірмою IBM, який мав довжину ключа 128 бітів. Алгоритм DES належить до класу шифрів Фейстеля із кількістю ітерацій 16, довжиною ключа 56 біта і довжиною блока 64 біта.
Хеш-функція - це перетворення, яке для вхідного значення повертає результат фіксованої довжини. Хеш-функціі тільки з цією властивістю мають багато застосувань при обчисленнях, але для криптографічного використання хеш-функції, як правило, повинні мати декілька додаткових властивостей.
Базовими вимогами до криптографічних хеш-функцій є такі:
•=> результат повинен обчислюватись для аргументу будь-якої довжини;
<=> алгоритм обчислення результату повинен бути відносно простим;
^> хеш-функція повинна бути одного напрямку;
<=> хеш-функція не повинна мати колізій.
Під тим, що хеш-функція повинна мати один напрямок, розуміється, що її важко обернути, тобто для заданого результату хеш-функціі неможливо (тут і далі мається на увазі неможливість практичного обчислення) знайти хоча б один відповідний аргумент.
Якщо для аргументу деякоі хеш-функції неможливо знайти інше значення її аргументу таке, що результат обчислення хеш-функції буде той же самий, то кажуть, що ця хеш-функція не має колізій в слабкому сенсі. Якщо для деякої хеш-функції неможливо знайти два різних значення аргументу, яким відповідає однаковий результат, то кажуть, що ця хеш-функція не має колізій у сильному сенсі.
Головні галузі застосування криптографічних хеш-функцій: ^перевірка цілісності повідомлень, ^цифровий підпис, ^цифрове маркування часу повідомлень. Будь-яка зміна в повідомленні під час його передачі з дуже великою ймовірністю призведе до зміни хеш-функції від цього повідомлення. Алгоритми генерації цифрових підписів, як правило, мають досить малу швидкість роботи, тому цифрові підписи ефективніше генерувати не від самого повідомлення, а від його хеш-функції. Крім того, значення криптографічної хеш-функції від повідомлення може розповсюджуватись, не знижуючи конфіденційності самого повідомлення. Це важливо для технологіі цифрового маркування часу повідомлень, коли необхідно забезпечити отримування часових відміток повідомлення, не відкриваючи його змісту.
Побудова більшості алгоритмів генерації криптографічних хеш-функцій, як правило, базується на визначенні хеш-функції в термінах так званої функціі компресіі. Функція компресії перетворює вхідне значення фіксованої довжини на вихідне значення меншої фіксованої довжини. Якщо маємо функцію компресії, то відповідна хеш-функція може бути визначена як повторення застосувань функціі компресії, доки не буде оброблене все повідомлення. Процес обробки повідомлення починається з того, що вхідне повідомлення довільної довжини розбивається на блоки, довжина яких визначається функцією компресії; перед цим повідомлення спеціальним чином вирівнюється на границю блока (із міркувань безпеки). Потім здійснюється послідовна обробка блоків, при якій вхідними даними для обробки кожного блоку є цей поточний блок і результат хешування попереднього блоку, а вихідним даним обробки останнього блоку - значення результату хеш-функції від повідомлення.
Алгоритм шифрування RSA. Алгоритм шифрування RSA відноситься до криптографічних систем із відкритим ключем. Криптосистеми з відкритим ключем (асиметричні криптосистеми) були розроблені в другій половині семидесятих років. В асиметричних криптосистемах процедури прямого і зворотнього криптоперетво-рення виконуються на різних ключах і не мають між собою очевидних і легковідсліджуваних зв 'язків, що дозволяють за одним ключем визначити інший. В такій схемі знання тільки ключа зашифрування не дозволяє розшифрувати повідомлення, тому він не є секретним елементом шифру і зазвичай публікується учасником обміну для того, щоб будь-хто бажаючий міг послати йому зашифроване повідомлення.
Принцип функціонування асиметричної криптосистеми полягає в наступному:
> користувач А генерує два ключі - відкритий (незасекречений)
і секретний - і передає відкритий ключ по незахищеному каналу
користувачу Б;
> користувач Б шифрує повідомлення, використовуючи відкритий
ключ шифрування користувача А;
> користувач Б посилає зашифроване повідомлення користувачу
А по незахищеному каналу;
> користувач А отримує зашифроване повідомлення і дешифрує
його, використовуючи свій секретний ключ.
Пари (відкритий ключ; секретний ключ) обчислюються за допомогою спеціальних алгоритмів, причому жоден ключ не може бути виведений з другого.
Криптографічна система RSA (Rivest-Shamir-Adleman). Авторами алгоритму RSA, запропонованого в 1977 p., є Р.Рівест (Rivest), А.Шамір (Shamir) і А.Адлеман (Adleman). Надійність алгоритму базується на складності факторизації (розкладення на множники) великих чисел і складності обчислення дискретних алгоритмів знахождення х при відомих a, b і п із рівняння:
![]()
Алгоритм RSA складається з трьох частин: генерування ключів, шифрування і дешифрування.
Генерування ключів. Оберемо два великих різних простих числа/? і q (Натуральне число називається простим, якщо воно ділиться тільки на себе і на 1. Додаток В.) та знайдемо їх добуток
![]()
Обчислимо функцію Ейлера![]() за формулою
за формулою
![]()
Таємний ключ добираємо з умов: ![]() і
і![]() взаємно просте з
взаємно просте з![]()
тобто d\j(n) не мають спільних дільників. Відкритий ключ є обираємо з умов:
![]()
Остання умова означає, що різниця де - 1 повинна ділитись на j(n) без залишку. Для визначення числа є слід підібрати таке число к, що:
![]()
В алгоритмі RSA (є, п)- відкритий ключ, (d,n)-секретний ключ.
Шифрування. Вихідне повідомлення розбивається на блоки М. однакової довжини. Кожен блок представляється у вигляді великого десяткового числа, менше п, і шифрується окремо. Шифрування блока М (М- десяткове число) здійснюється за наступною формулою:
![]()
де С- шифроблок, що відповідає блоку відкритого повідомлення М. Шифрблоки з'єднуються в шифрограму.
Дешифрування. При дешифруванні шифрограма розбивається на блоки відомої довжини і кожен шифрблок дешифрується окремо за наступною формулою:
![]()
Функція хешування. Функцією хешування називається перетворення даних, що переводить рядок бітів М довільної довжини в рядок бітів h (M) деякої фіксованої довжини (кілька десятків чи сотень біт). Хеш-функція h (M) повинна задовольняти наступним умовам:
■=> хеш-функція h (M) повинна бути чутливою до будь-яких змін вхідної послідовності М;
•=> для даного значення h (M) повинно бути неможливо знайти значення
м-
■^ для даного значення h (M) повинно бути неможливо знайти значення М №М таке, щоіі(М') =h(M) .
Ситуація, за якої для різних вхідних послідовностей М, М співпадають значення їх хеш-образів:
називається колізією.![]() При побудові хеш-образу, вхідна послідовність М розбивається на блоки А/ фіксованої довжини і оброблгється поблочно за формулою:
При побудові хеш-образу, вхідна послідовність М розбивається на блоки А/ фіксованої довжини і оброблгється поблочно за формулою:
![]()
Хеш-значення, що обчислюється при введенні останнього блоку повідомлення, стає хеш-значенням всього повідомлення. В якості прикладу розглянемо спрощений варіант хеш-функціїіз рекомендацій МККТТХ.509:![]()
де п = pq, piq- великі прості числа, HQ - довільний початковий вміст, А/ - /-тий блок повідомлення М-М1М2... Мк.
Електронний цифровий підпис. Цифровий підпис у цифрових документах грає ту ж роль, що і підпис, поставлений від руки в документах на папері: це дані, що приєднуються до повідомлення, котре передається, та підтверджують, що власник підпису склав чи завірив це повідомлення. Отримувач повідомлення за допомогою цифрового підпису може перевірити, що автором повідомлення є саме власник підпису і що в процесі передачі не було порушено цілісність отриманих даних.
При розробці механізму цифрового підпису виникають наступні задачі:
Р створити підпис таким чином, щоб її неможливо було підробити;
Р мати можливість перевірки того, що підпис дійсно належить вказаному власнику;
Р мати можливість запобігти відмові від підпису.
Класична схема створення цифрового підпису. При створенні цифрового підпису за класичною схемою відправник виконує наступне:
■=> застосовує до вихідного повідомлення хеш-функцію;
■=> обчислює цифровий підпис за хеш-образом повідомлення з використанням секретного ключа створення підпису;
о формує нове повідомлення, яке складається з вихідного повідомлення та доданого до нього цифрового підпису.
Отримувач, отримавши підписане повідомлення, виконує наступні дії:
> відділяє цифровий підпис від основного повідомлення;
Р застосовує до основного повідомлення хеш-функцію;
Р з використанням відкритого ключа перевірки підпису здобуває хеш-образ повідомлення з цифрового підпису;
Р перевіряє відповідність обчисленого хеш-образу повідомлення та добутого з цифрового підпису. Якщо хеш-образи співпадають, то підпис признається справжним.
Схема підпису RSA. Криптосистема з відкритим ключем RSA може використовуватись не лише для шифрування, але і для побудови схеми цифрового підпису. Для створення підпису повідомлення М відправник виконує наступну послідовність дій:
о обчислює хеш-образ r=h (М) повідомлення М за допомогою деякої хеш-функції;
■=> зашифровує отриманий хеш-образ г на своєму секретному ключі (d,n), тобто обчислює значення s- ґ'тоа'п, що і є підписом.
Для перевірки підпису отримувач здійснює наступне:
>розшифровує підпис s на відкритому ключі (е,п) відправника, тобто
обчислює г' = sf modn і таким чином відновлює імовірний хеш-образ г'
повідомлення М;
> обчислює хеш-образ h(M) —r повідомлення М за допомогою тієї
ж самої хеш-функції, котру використовував відправник;
> порівнює отримані значення г і г'. Якщо вони співпадають, то
підпис правильний, відправник дійсно є тим, за кого себе видає, і
повідомлення не було змінено при передачі.
