15.4. Аналіз економічних часових рядів методами нелінійної динаміки

15.4. Аналіз економічних часових рядів методами нелінійної динаміки

Стохастичні характеристики атракторів. Щоб схарактеризувати атрактори, корисно ввести поняття розмірності. Розмірність визначає кількість інформації, необхідної для визначення ко­ординат точки, що належить атрактору в межах заданої точності. У попередній темі було введено поняття фрактальної розмірності [див. (14.2)]. Більш строго, фрактальною розмірністю атрактора в n-вимірному фазовому просторі називають величину

,       (15.2)

де  — мінімальна кількість n-вимірних кубів з ребром r, необхідних для покриття атрактора.

Фрактальна розмірність дивних атракторів буде дробовою. Зауважимо, що у формулі для обчислення фрактальної розмірності однаково важливі всі непорожні n-вимірні куби. Це істотний недолік, оскільки дивні атрактори просторово неоднорідні, а деякі області атрактора відвідуються траєкторією частіше за інші. Отже, необхідно знати доволі довгу траєкторію, щоб гарантувати відвідування навіть малоймовірних кубів. З цією метою кожний непорожній куб доводиться зважувати за допомогою відносної частоти, з якою він відвідується типовою траєкторією. Розмірності, які визначаються з урахуванням імовірності відвідування траєкторією різних областей атрактора у фазовому просторі, називають імовірнісними.

Інформаційна розмірність атрактора визначається наступним чином:

,         (15.3)

де  — кількість інформації, необхідної для визначення стану системи в межах необхідної точності . Якщо атрактор просторово однорідний, то , інакше .

Інша розмірність, яка також належить до класу й, називається кореляційною та визначається співвідношенням:

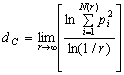,     (15.4)

де  — ймовірність того, що пара точок атрактора належить і-му кубу (імовірність того, що одна точка попаде в і-й куб, буде рі;
за припущення, що трапляння двох точок у і-й куб — незалежні події, імовірність цієї події становитиме ).

Кореляційну розмірність можна також подати у вигляді:

        (15.5)

де M — кількість спостережень,  — відстань між точками xi та xj, q — функція Хевісайда:

Величина  називається кореляційним інтегралом (сумою) та визначає ймовірність того, що відстань між двома точками xi та xj буде меншою за . Зауважимо, що всі три розмірності атракторів, які було розглянуто раніше, є частинними випадками розмірності Реньї:

.         (15.6)

При q = 0 розмірність Реньї збігається з фрактальною розмірністю, при q = 1 — з інформаційною, при q = 2 — з кореляційною розмірністю. Для цілих q розмірність Реньї має таку інтерпретацію: великі додатні q визначають області атрактора, які відвідуються найчастіше, а великі від’ємні значення визначають області, що майже не відвідуються. Таким чином, діапазон розмірності Реньї можна розглядати як характеристику ступеня просторової неоднорідності атракторів.

Алгоритми реконструкції атракторів. Одним із перспективних напрямків досліджень у рамках нелінійної динаміки є розроб­ка так званих «алгоритмів реконструкції атракторів». Це но-
вий клас методів обробки часових рядів, породжуваних детермі­нованими динамічними (хаотичними) системами. Головна ідея застосування цих методів полягає в тому, що основна структура хаотичної системи, яка містить всю інформацію про систему, а саме атрактор динамічної системи, може бути відновлена через спостереження поводження самої цієї динамічної системи, фіксованої як часовий ряд.

Розглянемо ідею методу Грасбергера і Прокачі (Grassberger, Procaccia), відповідно до якого процедура реконструкції фазового простору і відновлення хаотичного атрактора системи зводиться до побудови лагового простору. Припустимо, що даний часовий ряд породжено деякою хаотичною динамічною системою. Припустимо, що m — найменша розмірність фазового простору, в який можна «занурити» реальний атрактор динамічної системи.

Тоді за допомогою часового ряду Xn, n = 1,2, ... N, «відновлений» атрактор формується з векторів Yn = (Xn, Xn-1, ..., Xn-(m-1)) у m-вимірному просторі, що називається лаговим простором досліджуваного часового ряду. Якщо часовий ряд справді є спостережуваною «проекцією» хаотичної динамічної системи, то згідно з теоремою Такенса реальний атрактор динамічної системи і «атрактор», відновлений у лаговому просторі за часовим рядом згідно з наведеним щойно правилом, у разі адекватного добору розмірності вкладення m матимуть однакові узагальнені фрактальні розмірності, показники Ляпунова та інші числові характеристики.

Якщо ж аналізований часовий ряд є реалізацією випадкового процесу, то відновлений «псевдоатрактор» являтиме собою без-
структурну хмару точок, яка у процесі послідовного збільшення розмірності вкладення лагового простору m, неначе газ, заповнюватиме весь наданий йому об’єм.

Один із тестів, що застосовується на практиці для з’ясування на­явності хаотичної детермінованості в досліджуваному часовому ряді (наприклад, індексах акцій, валютних курсів та ін.), полягає у вивченні властивостей кореляційної суми (інтеграла) Cm(r) і поводження кореляційної розмірності dC залежно від розмірності вкладення m. Як уже зазначалося, кореляційний інтеграл Cm(r) — це ймовірність того, що дві точок на відновленому атракторі в m-вимірному лаговому просторі містяться в межах відстані r одна від одної.

Якщо графік функції logCm(r) відносно log(r) має чітко виражену лінійну ділянку, це вказує на самоподібну геометрію (топологію) атрактора, що, у свою чергу, говорить про хаотичний характер поводження системи, яка «породжує» цей часовий ряд. Кореляційна розмірність обчислюється як середній нахил зазначеного графіка, а помилка обчислення береться як половина різниці максимального і мінімального нахилу. Зі зростанням розмір­ності вкладення кореляційна розмірність збільшується. Однак
для хаотичних даних кореляційна розмірність буде зрештою насичуватися при її справжньому значенні.

Для випадкових даних такого насичення не спостерігається і кореляційна розмірність зростатиме монотонно. Таке поводження кореляційної розмірності пояснюється тим, що в рамках методу Грасбергера—Прокачі кореляційна розмірність для реальних хаотичних систем є непоганим наближенням для фрактальної розмірності дивного атрактора. Фрактал, вкладений у простір з вищою розмірністю, зберігає свою справжню розмірність через нелінійні кореляції між точками. Тому для детермінованого хаотичного часового ряду кореляційна розмірність збігається до свого справжнього значення. Водночас для випадкової послідовності точки відновленого «псевдоатрактора» утворять безструктурну хмару в лаговому просторі незалежно від його розмірності.

Отже, методи реконструкції атракторів дають змогу з’ясувати, наскільки складною має бути модель досліджуваної системи (скіль­ки в неї має бути ступенів волі або параметрів порядку, наскіль-
ки тривалим може бути часовий інтервал, на якому можна прогнозувати поводження цієї системи).

R/S аналіз. Поряд із кореляційним та спектральним аналізом одним із потужних методів дослідження довготермінової пам’яті в часових рядах та з’ясування ступеня їхньої фрактальності є застосування R/S-аналізу (Rescaled Range Analysis), який був запропонований Херстом (Hurst) у гідрології під час вивчення коливань річкових стоків. Б. Мандельброт узагальнив метод Херста з метою дослідження часових рядів довільної природи. Ідея цього методу полягає у вимірюванні зміни з часом рівня нагромадження відхилень від середнього значення часового ряду [9; 12]. Було з’ясовано, що для деяких часових рядів залежність R/S від кількості спостережень N має такий емпіричний закон розподілу:

,

де  — константа; N — кількість часових періодів спостережень, Н — експонента Херста.  визначається так:

,

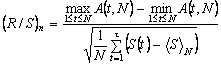де A(t, N) — нагромадження відхилення часового ряду S(t) від середнього за N періодів :

.

Якщо показник Н приблизно дорівнює 0,5, то це свідчить про те, що ряд описує випадкове блукання. Коли Н відрізняється від 0,5, то це означає, що спостереження не незалежне. Тобто кожне спостереження містить «пам’ять» про минулі спостереження, минуле поводження ряду, причому не короткотермінову, а саме довготермінову пам’ять.

Якщо 0 £ H £ 0,5 — то ряд буде від’ємно корельованим (антипер­систентним), тобто якщо спостерігалася тенденція зростання ряду в минулому, то варто очікувати надалі на його спадання. А якщо 0,5 £
£ H £ 1 — ряд буде додатно корельованим (персистентним), або трендостійким. Тобто якщо ряд зростає (спадає) в минулому, то ймовірно, що така сама тенденція збережеться протягом деякого часу в майбутньому. Показник Херста пов’язаний із фрактальною розмірністю співвідношенням: .

На практиці для оцінювання показника H часто використовують метод, який полягає в побудові функції лінійної регресії . Якщо побудувати графік цієї регресії в подвійних логарифмічних координатах, то оцінкою показника Херста в цьому випадку буде коефіцієнт нахилу H цієї прямої.

Дослідження, проведені останнім часом (див., наприклад, [9]), свідчать, що багато фінансово-економічних часових рядів, таких як курси акцій, валютні курси, фондові індекси та інші економічні індикатори, мають статистику Херста більш як 0,5, тобто мають фрактальну структуру, або довгострокову пам’ять.

Контрольні запитання та завдання

У чому полягає принцип підпорядкування Хакена?

Як ви розумієте термін «параметри порядку»? Наведіть приклади.

Що характеризують показники Ляпунова?

Чим відрізняється фрактальна розмірність атракторів від імовірніс­ної розмірності?

Доведіть, що інформаційна, кореляційна та фрактальна розмірності є частинним випадком розмірності Реньйі.

Опишіть сценарій Фейгенбаума переходу до хаосу.

У чому полягає ідея методів реконструкції атракторів?

Як розраховується і що дає змогу з’ясувати статистика Херста?