16.1. Моделювання хаотичної динаміки в економіці

16.1. Моделювання хаотичної динаміки в економіці

Сучасна економіка як складна система розвивається нерівномірно, їй притаманні як режими стійкого функціонування, так і режими хаотичної динаміки. Останнім часом економісти намагаються інтерпретувати хаотичні явища в економіці в термінах детермінованих систем, серед яких широко використовуються дискретні відображення, розглянуті в попередній темі. Так, логістичне відображення та його модифікації завдяки їхнім універсаль­ним властивостям і здатності описувати процеси з доволі склад­ною динамікою широко використовуються в побудові моделей економічної динаміки на макро- і мікрорівні. Розглянемо кілька прикладів використання цього відображення в економіці.

Приклад 1. Класичне логістичне відображення

,      (16.1)

яке в біології використовується для аналізу зростання чисельності популяції, можна застосовувати під час дослідження динаміки зростання малих підприємств. Як було показано в попередній темі, за певних умов у такій системі виникає множина біфуркацій подвійного періоду, а при великих n у системі виникає хаос.

Або в моделі адаптації фірми в ринкових умовах [12] її стратегію можна описати логістичним рівнянням:

,          (16.2)

де хt — рівень доходу фірми в момент часу t; l — параметр, що залежить від тривалості виробничого циклу та характеризує певний спосіб виробництва; L — рівень прибутку, необхідний для того, щоб обсяги продажу в майбутньому забезпечили нормальний рівень прибутку; H — максимальний рівень прибутку. Можна показати, що рівняння (16.2) зводиться до класичного логістич­ного відображення, і тому при деяких значеннях параметрів ця
модель описує хаотичне поводження системи.

Приклад 2. Процеси ціноутворення в павутиноподібній моделі фірми можна також розглядати за допомогою логістичного відображення [1]. Оскільки залежність надлишкового попиту D на товар від його ціни P можна описати рівняннями:

,

,

де q — кількість товару; H — функція корисності, то максимум функції корисності досягається при . При великому l на ринку виникає хаос у поводженні цін.

Приклад 3. Аналогічну модель можна побудувати для інвестиційної динаміки. Зі зростанням інвестицій економіка наближається до інвестиційного бар’єру. Лаг між інноваціями та їх реалізацією зменшується. При цьому зменшується можливість апро­бування альтернатив і зростає загальна невизначеність. Орієнтація на поточну кон’юнктуру спричинює надлишок капіталу, зниження темпів виробництва та продуктивності, що може призвести до інвестиційної кризи на ринках капіталу. Логістичне відображення можна також використовувати в дослідженні критичних режимів та хаосу на фондових і валютних ринках [9].

Приклад 4. Розглянемо модель самоорганізації ринку праці, динаміка якої залежить від кількості зайнятих у галузі  у пев­ний момент часу. Передбачається, що місткість ринку праці ста-
ла й дорівнює , тоді  — кількість потенційних безробітних або кількість вільних робочих місць. Розглядаються ймовірність того, безробітний знайде роботу в проміжку часу , яка залежить від кількості вільних робочих місць , та ймовірність звільнення, що залежить від кіль­кості вільних робочих місць . Вва-
жається, що . Тоді рівняння моделі має вигляд:

.  (16.3)

Можна показати, що існує лінійна заміна змінних, яка приводить рівняння (16.3) до класичного логістичного відображення (16.1).

Приклад 5. Деякі моделі мають форму, схожу на рівняння класичного логістичного відображення. Розглянемо, наприклад, макроекономічну модель зростання, запропоновану Хаавельмо [2]:

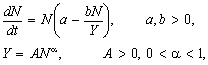
де N — чисельність населення; Y — реальний обсяг виробництва; a, b, A, a — константи. Після підставлення другого рівняння в перше дістанемо:

.

Увівши дискретний час та замінивши похідні першими різниця­ми, після заміни змінних запишемо:

,

де нова змінна визначається співвідношенням

.

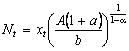Отже, можна побачити, що закон зростання являє собою узагальнення логістичного відображення.

Якщо взяти, скажімо, a = 1/2, то для a < 4 рівновага буде стійкою, тобто вона досягається будь-якою траєкторією, що починається в довільній точці. Але при 4 < a < 5,75 траєкторії не будуть рівноважними, а залишатимуться в області, обмеженій нулем та одиницею. Фактично тільки-но параметр a > 4, нестійка точка рівноваги розпадається на дві стійкі точки з періодом два, тобто відбуваються біфуркації подвійного періоду. При значеннях параметра, що перевищують 4,8, двоперіодичний цикл стає нестійким, і кожна двоперіодична точка розпадається на дві чотириперіодичні точки.

Зі зростанням a цей біфуркаційний процес триває, генеруючи невироджені орбіти періоду 2k (k = 2, …). Область, усередині якої зароджуються стійкі орбіти періоду k, які далі стають нестійкими та розпадаються на 2k-періодичні орбіти, обмежена значенням параметра  (точне його значення невідоме). Інтервал  називають областю хаосу.

У цьому підрозділі ми розглянули приклади застосування для моделювання хаотичної динаміки в економічних системах однієї з найпростіших нелінійних моделей — логістичного відображення. Зрозуміло, що для побудови адекватних моделей економічної динаміки часто доводиться застосовувати складніші моделі, наприклад багатовимірні відображення, системи нелінійних диференціальних рівнянь [1; 2; 7; 9; 12; 13]. Зокрема, у монографії [12] розглядаються властивості узагальненого логістичного відображення, що задається рекурентним співвідношенням

і наведено приклади його використання в моделюванні економічної динаміки.

Розглянуті приклади показують, що процеси, які описуються навіть простими нелінійними моделями, при деяких значеннях параметрів мають хаотичне поводження, яке здається випадковим і може помилково пояснюватися дією неврахованих або випадкових факторів. Але в детермінованих нелінійних моделях хаос породжується саме нелінійністю. З цього випливає, що під час побудови моделей економічної динаміки введення теоретично обґрунтованих нелінійних залежностей поряд із використанням випадкових змінних дає змогу успішно пояснювати різноманітні економічні флуктуації.