2.2. Перспективна оцінка чисельності і структури населення регіону

2.2. Перспективна  оцінка  чисельності і структури  населення  регіону

Результати аналізу демографічної структури населення регіону у подальшому використовуються для визначення перспективної кількості населення та його можливої зміни в майбутньому. Для цього за допомогою методів регресивного і кореляційного аналізу проводиться порівняння зміни чисельності населення пев­ного регіону і регіону-еталону в статистичній формі. Важливим при цьому є з’ясування статистичного зв’язку між зростанням населення і факторами, які його зумовили: кількість зайнятих, інвестиції, дохід, експорт, щільність населення, розміри сімей, квартирна плата тощо. За такого роду аналізу зміна чисельності населення звичайно розглядається як залежна змінна, а всі інші фактори — як незалежні змінні.

Для аналізу зростання населення використовуються відомі прийоми математичної статистики. Розглянемо деякі з них.

1. Проста регресія. Зростання населення приймається за залежну змінну, а один з факторів — за аргумент. Для даної множини спостережень досліджується зв’язок між значеннями, які приймають обидві змінні. Найпростіша форма зв’язку відображається графіком лінійної регресії, побудованим за існуючими показниками, незалежно від того, належать вони до минулого чи теперішнього часу. Рівняння отриманої прямої має вигляд:

де Р —досліджувана кількість населення регіону, що вивчається; a — фактична кількість населення в базовому році; b — середньорічний приріст. Розраховується за даними минулого періоду, який дослідник вважає показовим. Обидві величини є постійними; X — значення, якого набуває незалежна змінна. Звичайно кожне спостереження (тобто точка на графіку) показує значення як Р, так і Х, в один і той самий заданий момент, тому якщо для прогнозу задана величина , то отримуємо рівняння:

.

У деяких випадках виникає необхідність порівняння величин Р і Х в різні моменти часу. Наприклад, величину Р для будь-якого року можна зіставити з величиною Х за минулий рік. У даному разі матимемо модель із запізнюванням і прогноз кількості населення на будь-який майбутній період:

.

У випадках, коли величина b в таких рівняннях є позитивною, кореляція також позитивна; якщо величина b негативна, то й кореляція негативна. При застосуванні цього методу розраховується також коефіцієнт кореляції, необхідний для показу, якою мірою лінія регресії пояснює відхилення індивідуальних значень залежностей змінної від їх середнього значення.

2. Множинна регресія. При проведенні регіональних досліджень часто з’ясовується, що приріст населення одночасно пов’я­заний з дією декількох факторів. У таких випадках необхідно застосовувати множинну регресію (кореляції). Рівняння лінійної регресії тут матиме такий вигляд:

,

де — значення, яких набуває кожна незалежна змінна, а — постійні позитивні чи негативні коефіцієнти. Кожний з них демонструє, яку зміну кількості населення мож­на пов’язати зі зміною на одиницю кожного фактора, якщо одночасно враховувати і вплив всіх останніх незалежних змінних.

3. Коваріаційний аналіз. Регресійний аналіз є придатним для пояснення деяких відхилень приросту населення від середніх значень у різні періоди або на різних територіях. Однак дуже часто переважну частину загального відхилення неможливо пояснити. Для того, щоб скоротити «непояснену» частину, проводять коваріаційний аналіз, основи якого проілюстровані схематично на рис. 2.1. На графіку залежна перемінна, скажімо населення, відкладається на вертикальній осі, а значення фактора Х (незалеж­ної змінної) — вздовж горизонтальної осі. Для деякого заданого моменту відкладаємо по кожному регіону чисельність населення і значення фактора Х. Розраховуємо також середню чисельність населення для всіх регіонів і заносимо цю просту середню величину у діаграму у вигляді горизонтальної лінії. На діаграму нанесено також по одній вертикальній лінії для кожного спостереження. Ці лінії показують відхилення чисельності населення в регіоні від середньої величини. За спеціальною термінологією це означає сумарне відхилення, мірилом якого служить сума квадратів вертикальних відхилень кожного спостереження до загальної середньої.

На рис. 1в робиться перша спроба такого пояснення. Фактор Х приймається за незалежну перемінну, яка пояснює ці відхилення. Дані рис. 1а відтворені на рис. 1б, де на їх основі проведена крива регресії, вирівняна методом найменших квадратів. Цей метод дає лінію, яка мінімізує суму квадратів відхилень значень залежної перемінної, якщо ці відхилення замірюються за вертикалями від лінії регресії. У даному разі загальне непояснене відхилення являє собою суму квадратів індивідуальних відхилень. Вертикальна лінія для кожного спостереження дає величину відхилень фактичної чисельності населення певного регіону від його теоретичної чисельності, яка представлена лінією регресії. Крива регресії є пояснювальною кривою в статистичному значенні цього поняття, тобто вона роз’яснює відхилення чисельності населення через відхилення значень фактора Х. Відхилення на рис. 1а і на рис. 1б, разом узяті, дають уявлення про сумарне відхилення, що не піддається поясненню. Оскільки у середньому відхилення на рис. 1б помітно менше, ніж на рис. 1а, то таким чином сумарна величина непоясненого відхилення зменшена.

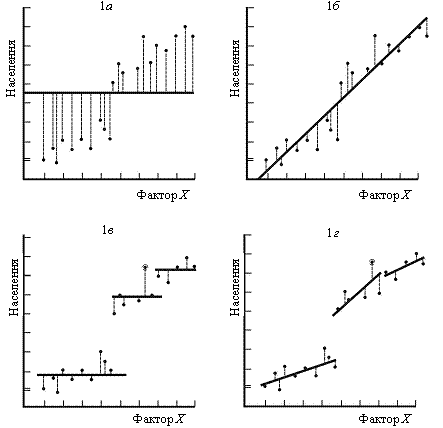
Рис. 2.1. Гіпотетичний приклад застосування коваріаційного
аналізу для перспективної оцінки кількості населення

У деяких випадках для зменшення сумарного непоясненого відхилення можна користуватися й іншим способом. Якщо при класифікації даних виходити з якого-небудь суттєвого фактора, який не піддається кількісному виразу, то точки будуть розташовані у вигляді кількох нагромаджень. Наприклад, на рис. 1а спостереження, які нанесені на нижню ліву частину поля, можуть належати до регіонів, що розташовані на півдні країни; спостереження, які згруповані в центральній частині поля, вище середньої лінії — до північних районів, а п’ять спостережень у правій частині поля — до західних регіонів країни. У такому разі слід знайти середнє значення для територіальних зон кожного метарегіону (середнє в підгрупі) і зобразити його горизонтальною лінією (рис. 1в). Відхилення чисельності населення кожного регіону від його середньої величини позначено пунктирною лінією. При порівнянні відхилень, які показані на рис. 1а і 1в, з’ясовується, що введення середніх величин у підгрупі знизило сумарне відхилення, яке не можна пояснити. Таким чином, певна частина повного відхилення, яке показане на рис. 1а, пояснюється через відхилення середніх величин у підгрупах на рис. 1в, тобто за допо­могою регіонального фактора. Однак такий дисперсійний аналіз не пояснює, чому середні значення за метарегіонами неоднакові і чому отримані саме такі їх значення, а не інші. Отже, такий дисперсійний аналіз дає лише статистичне пояснення явища, а не його теоретичне або причинно-наслідкове пояснення.

Якщо існують два підходи, кожний з яких незалежно від іншого приводить до скорочення частини повного відхилення, яке не можна пояснити, то логічно припустити, що застосування обох прийомів одночасно дасть можливість досягти ще більшого скорочення частини, яка не підлягає поясненню. Саме таке поєднання різноманітних прийомів і називається коваріаційним аналізом. Його результати представлені на рис. 1г, де дані згруповані за метарегіонами. Однак у даному разі, замість того, щоб визначати середні показники по кожній підгрупі, для будь-якої з них за точками накреслюється своя пряма одинична регресія. У випадках, коли крім фактора Х, враховуються й інші незалежні перемінні, одержується лінія множинної регресії. Відхилення фактичної чисельності населення якого-небудь регіону від теоретичного значення, отриманого на основі лінії регресії для даного регіону, показано на рис. 1г пунктирною вертикальною лінією. Помітно, що розміри відхилень менші, ніж у будь-якому іншому графіку, що означає ще більше скорочення частки повного відхилення, яке неможливо пояснити. Таким чином, ця методика засвідчує, що при розгляді регіонального фактора у поєднанні з іншими чинниками, які піддаються кількісному виразу, можна отримати краще пояснення статистичних явищ, ніж при відокремленому їх розгляді.

Звернемося тепер до аналізу складових частин приросту населення, а саме: природного приросту, балансу міграційних потоків, приєднання нових або втрати старих територій. Останній з перелічених елементів має значення лише у випадках, коли йдеться про адміністративно-територіальні одиниці, скажімо про міста, причому цей елемент можна розглядати як особливий випадок, пов’язаний з міграцією населення. Основну залежність у найзагальнішому вигляді можна уявити таким рівнянням:

де Nn — природний приріст населення за період ; Mn — міграційний баланс за той самий період.

При аналізі складових приросту застосовуються методи, які ґрунтуються на природному прирості, і методи, які враховують приплив і відтік населення з регіону. Методи, що засновані на природному прирості, найменш досконалі. Їх використовують лише при аналізі складових приросту населення. Міграції населення при цьому зовсім не враховуються, виходячи з припущення, що припливу і відтоку немає або що ці процеси взаємно врівноважені. Таким чином, до уваги беруться лише біологічні фак­тори зростання населення.

Отже, перспективні оцінки кількості населення розраховуються на основі рівняння:

де  — очікуваний коефіцієнт народжуваності за період ;  — очікуваний коефіцієнт смертності за той самий період.

Точнішим варіантом даної методики є так званий метод групового виживання (cohort-survival method). Він враховує розбіжності в рівнях народжуваності і смертності між окремими віковими, статевими і національними групами. Початково населення поділяють на вікові групи, як правило, з інтервалом 5 років, враховуючи стать і національність. На основі спеціальних таблиць смертності за віковими групами або тривалості життя для різного віку підраховують кількість людей, що вижили в кожній з таких груп з інтервалами від 1 року до 5 років. Для кожного з інтервалів наводиться особливий прогноз природного приросту населення, який формується таким чином. По-перше, шляхом множення коефіцієнта народжуваності для даної вікової групи на середню кількість жінок, здатних до народження дітей, у кожній з цих груп, знаходять передбачувану кількість народжених. По-друге, підраховують, яка кількість народжених дітей виживає за вживаних показників дитячої смертності. Кількість немовлят, що вижили у найнижчій віковій групі, додають потому до раніше підрахованої кількості дітей, що вижили в інших вікових групах. Такий підрахунок повторюють для кожного з прийнятих інтервалів аж до дати, на яку дається прогноз. Звичайно цей метод не є досконалим, оскільки отримані результати не можуть бути точнішими за показники народжуваності і смертності, які були прий­няті на період, для якого розробляється прогноз. У тих випад-
ках, коли показники природного приросту досить точно відомі, а баланс міграцій населення наближується до нуля, можна вважати, що приплив і відтік населення майже не позначаються на кількості і структурі населення. Даний метод може ефективно використовуватися, особливо коли метою аналізу є отримання даних про склад населення у майбутньому.

Наведені методи можна розширити таким чином, щоб вони враховували вплив міграцій населення. При цьому приплив населення визначається як сума народжуваності і міграційного приросту, а скорочення — як сума кількості смертей і відтік у зв’язку з міграціями. Тоді рівняння набуває вигляду:

де  — народжуваність населення за період n;  — смертність населення за той самий період;  — міграційний приплив населення за період n;  — міграційний відтік населення за той самий період.

Незалежно від того, який з даних методів, заснованих на природному прирості, вибирається як вихідний, необхідно насамперед дати прогноз міграціям, з тим щоб потім розповсюдити відповідні показники народжуваності і смертності.

Прогноз абсолютних або відносних розмірів майбутніх міграційних потоків можна отримати різними методами, наприклад екстраполяцією, методом експертних оцінок та іншими, або використовуючи їх у комплексі.