2.2.3.1.7. Стохастичне прогнозування

Основою прийняття оптимальних рішень менед­жером СР є вміння оперативно виявляти тенденції розвитку соціаль­них процесів і своєчасно реагувати на них, передбачаючи небажані для суспільства та індивидів наслідки. В будь-яких сферах діяльності людини виникають ситуації, коли за наявною інформацією {X} по­трібно спрогнозувати (передбачити) деяку величину Y, стохастично пов'язану з {X}. Наприклад, якщо {X} належить до теперішнього часу, а У — до майбутнього. Скажімо, за даними динаміки вартості спо­живчого кошика оцінюється ставлення людей до здійснених реформ.

Завдяки широким можливостям графічного подання даних в MS Excel та системі STATISTICA можна будувати інтуїтивні передба­чення вже на підставі відповідно поданої первісної інформації у ви­гляді графіків та діаграм [25]. Наприклад, здібності індивіда до досяг­нення успіху, до управління та ефективного керівництва, комуніка­бельність та інші риси, кваліметровані за допомогою тестування, можна подати у вигляді пелюсткової діаграми і за формою цієї діаграми ("ділового профілю") легко порівнювати кандидатів на посади менед­жерів СР. Аналітики фінансових ринків успішно використовують методику так званого технічного аналізу, в основу якої покладені графічні образи різних біржових ситуацій, що простежуються за часо­вими залежностями котирування цінних паперів (дивись, наприклад, ППП MetaStock). Відповідні інструменти графічного аналізу є в MS Excel та в системі STATISTICA. До них насамперед належать візуалізація координат точок на графіках; побудова прямих, що прохо­дять через дві вибрані точки, прямокутників, еліпсів, кіл і фрагментів цих фігур; виконання поворотів і відображень; з'єднання точок плав­ними кривими (сплайнами) тощо. Однак не слід забувати, що корисна інформація, особливо в СР, вельми "зашумлена", тобто обтяжена знач­ною випадковою складовою. Тому використання її у "сирому" ви­гляді для прийняття рішень може призвести до помилок.

Раніше вже згадувалося, що точки лінії емпіричної регресії (трен-ди, або характеристики основної тенденції) по суті — прогнози зна­чень результативної ознаки. В STATISTICA вони так і називають­ся — Predict Depenent Var — передбачене значення залежної змінної. Однак нас більше цікавить екстраполяція (подовження) кри­вої регресії за область визначення незалежної змінної. В MS Excel для цього на вкладці Параметры діалогового вікна Линия тренда

передбачені лічильники кількості кроків (періодів, або горизонту) про­гнозу вперед і назад, після установки яких лінія тренду автоматично подовжується за межі крайніх значень незалежної змінної. Для про­гнозування за ЛОМ у MS Excel використовують функції ПРЕД-СКАЗ і ТЕНДЕНЦИЯ. Останню можна також застосовувати для поліноміальних моделей. Крім того, в MS Excel існує процедура ав­томатичного заповнення діапазону комірок на підставі даних, записа­них у перші дві комірки рядка або стовпчика. При цьому, якщо мар­кер блоку цих комірок "протягається" у бік розширення блоку, то комірки, що включаються до нього за умовчанням, заповнюються зна­ченнями, розрахованими за арифметичною прогресією, а в разі видачі команди Правка/Заполнить/Прогрессия можна використати також геометричну прогресію. Таким способом вдається побудувати лінійний та експоненціальний прогнози на кілька кроків уперед.

В системі STATISTICA прогнозування з використанням рівнянь регресії принципово не відрізняється від викладеного. Слід врахову­вати, що найнадійніший прогноз дає прямолінійна регресія на один — два кроки вперед, але він найменш точний, бо коридор помилок ре-гресійної прямої завжди ширший порівняно з кривими вищих по­рядків. З іншого боку, підвищення порядку, наприклад, поліноміальної моделі, приводить до зниження залишкової дисперсії, але потребує обережнішого ставлення до якості прогнозу.

Дотепер вважалося, що функція розподілу генеральної сукупності не змінюється з перебігом часу або досліджується один часовий зріз (момент) досліджуваного процесу. Проте реально часто доводиться мати справу з нестаціонарною ситуацією коли параметри ЗРЙ змінюються і час стає одним з факторів, від якого залежать значення як результа­тивної змінної, так і інших факторів. Підтримка управлінських рішень за таких обставин повинна ґрунтуватися на аналізі та прогнозуванні часових рядів, або рядів динаміки (РД).

Використання для прогнозування РД розглянутих методів регре-сійного аналізу виправдане тільки за умови ергодичності процесу, коли усереднення за сукупністю можна замінити усередненням за часом, тобто для стаціонарних РД, у яких ЗРЙ, пов'язаний з випадковим процесом {Y.(t)} (—°° < t < 00), не залежить від вибору початку відліку часу t0.

В аналізі РД кожна окрема функція Y.(t), де t — незалежна змінна, а і — фіксоване, називається вибірковою функцією. Для кожного но-

мера вибірки і реалізації процесу Y.itJ, Y.(t2), ..., Y.(tN) являють собою ./V випадкових величин, залежних від і, і висувається припущення, що для будь-якого ./V існує певний Л^-мірний ЗРЙ. Ми зупинилися на цих визначеннях, ризикуючи обтяжити виклад математичними подроби­цями, щоб читач зрозумів походження понять автоковаріація та авто-кореляція, які ми будемо використовувати надалі. Префікс "авто-" означає, що зв'язки виявляються усередині РД через реалізації, відділені одна від одної проміжком х, який називається часовим лагом (за­тримкою): tx = t і t2 = t + + х. В термінах математичної статистики автокореляція обчислюється за формулою

де \iY(t) = E[Y.(t)] — математичне очікування значення У. в момент часу t; визначається усередненням за сукупністю т спостережень в момент t:

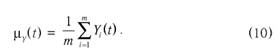
Для стаціонарних випадкових процесів £[У(ґ)] = E[Y(t + х)] = = const, тому

а вся послідовність значень {с.(х)} називається автоковаріаційною функцією Суу(х), або просто коваріацією стаціонарного РД. За умови х = 0, маємо

тобто коваріація стаціонарного процесу з нульовим лагом збігається з його дисперсією. Відношення

називається автокореляцією (корелограмою), а сукупність {correl.(Yt+^, Yt)} — автокореляційною функцією RYY(x). Якщо середнє процесу дорівнює нулю, то автокореляційна функція збігається з автоковарі­аційною.

Коли одночасно спостерігаються два процеси {X.(t)} та {У.(ґ)}, то окрім відповідних функцій Схх(х), Rxx(i), CYY(x) та RYY(x) можна розра­хувати взаємні коваріаційну та кореляційну функції

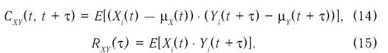
Два стаціонарних процеси вважаються некорельованими, якщо CXY(x) = 0 для усіх t. Коли Rxy(t) = 0, стохастичний зв'язок між двома стаціонарними процесами відсутній тільки за умови, що хоча б одне із середніх ц^або |л.у дорівнює 0.

Особливістю прогнозування РД є та обставина, що з часом інфор­мація в них постійно поповнюється, а попередні спостереження "ста­ріють". У зв'язку з цим прогноз РД за допомогою описаного класич­ного КРА на момент накопичення потрібного обсягу інформації може стати неактуальним. Проблема знімається за допомогою рекурентних алгоритмів мінімізації середніх квадратичних помилок прогнозу, в яких враховується автоковаріаційна структура РД, а коефіцієнти мо­делі перераховуються на кожному черговому кроці (додавання да­них). Дуже популярна також процедура побудови прогнозу, що скла­дається з усереднення всіх минулих значень РД з геометрично або експоненціально спадними статистичними "вагами". До моделей РД, в яких реалізовано ці принципи, належать процеси ковзного серед­нього (порядку q) (KC(q)); інтегрованого КС (ІКС); авторегресії (по­рядку р) (АР(р)); змішані моделі АРКС(р, q) та АРІКС (р, q). Останні застосовуються для прогнозування нестаціонарних РД.

В MS Excel реалізовані дві моделі РД: КС та експоненціального згладжування (ЕЗ). Інструмент КС — це середнє арифметичне, яке розраховується за даними ./V попередніх спостережень, що утворюють часове "вікно" КС, яке зсовується ("сковзає") по часовій шкалі на один період вперед на кожному наступному кроці розрахунку:

де: / — "вік" даних.

Величина N визначає ширину "вікна" КС. Прогнозом методу КС на один період вперед служить попереднє значення КС. Як правило, прогноз КС справджується краще, ніж прогноз за середнім рівнем РД, і значно краще, ніж "наївний" прогноз, що дорівнює значенню попе­реднього періоду. Ковзне середнє працює з даними, отриманими з однаковим часовим кроком (періодом дискретизації). На відміну від КРА метод КС не дає можливості отримати математичний опис плавної лінії розвитку РД (тренду). КС часто використовують для зглад­жування РД, очищення від випадкової складової (фільтрації РД), тому що КС "реагує" на немонотонності, які мають розмір його "вікна". Це доводиться враховувати, коли КС застосовують для прогнозування коливальних процесів, наприклад пов'язаних із сезонною періодичніс­тю. Розрахунок значень КС у MS Excel супроводжується також розра­хунками стандартних похибок прогнозу.

Метод ЕЗ призначається для передбачення наступного значення на основі прогнозу для попереднього періоду, скоригованого в бік зменшення його похибки

де символ   означає прогноз.

У моделі ЕЗ статистичні "ваги", приписувані спостереженням, ек­споненціально спадають залежно від величини лагу. Але, на відміну від КС, у розрахунках використовують всі попередні спостереження, жодні з них не виключаються. Константа згладжування у* визначає, наскільки сильно впливають на прогнози похибки у попередньому прогнозі. Звичайно у задають на рівні 0,2-0,3. Інакше кажучи, помил­ка поточного прогнозу планується на 20-30 % від помилки поперед­нього. Чим більше у, тим точніше прогноз відтворює останні значен­ня ДР, але збільшення у може призвести до непередбачених сплесків. Із зменшенням у прогноз все більше відстає від останніх значень. Це приводить до згладжування різких переходів та їх часового зміщен­ня. Добрі прогнози виходять тоді, коли останні результати спостере­жень відбивають довільні (випадкові) коливання, які довго не зміню­ють загального рівня РД. Якщо виникає враження, що при у > 0,3 результат поліпшується, то найімовірніше, ще це відбувається за раху­нок високої автокореляції. В такому разі кращі результати дають АР-моделі. Для цього слід використовувати систему STATISTICA.

Аналіз і прогнозування РД (АПРД) у STATISTICA здійснюється з використанням модуля Time SeriesAnalysis/Forecasting (Аналіз часових рядів /Прогнозування). Модуль містить різні види згладжу­вання: КС, ковзне медіанне (КМ), ЕЗ, а також перетворень і нормування. Основними компонентами модуля є Лй/МА-модель АРІКС; Interrupted time series analysis (Аналіз перерваного часового ряду) — моделі

Величину 1 — у називають фактором загасання.

ARIMA з інтервенцією; Exponential smoothing & forecasting

(Експоненціальне згладжування та прогнозування); Seasonal decomposition (1,2) (Сезонне розкладання (1, 2)); Distributed lags analysis (Аналіз розподілених лагів) та Spectral (Fourier) analysis — спектральний (Фур'є) аналіз.

Аналіз і прогнозування рядів динаміки починається на стартовій панелі ARIMA з обчислень Autocorrelations (Автокореляції) або Partial autocorrelations (Часткові автокореляції). Користувач може проаналізувати оцінки Схх і CXY в числовому форматі або у вигляді графіка і визначити, наскільки РД близький до стаціонарного. Потім задаються параметри моделі ARIMA (APIKC): p-Autoregressive — параметр АР (регулярний); P-Seasonal — сезонний параметр АР; q-Mouving average — параметр КС (регулярний) та Q-Seasonal — сезонний параметр КС. Задания значень параметрів є відповідаль­ним моментом, оскільки це, по суті, — ідентифікація моделі РД.

Коефіцієнти АРІКС-моделі РД у системі STATISTICA визнача­ються за допомогою процедури Estimation ofMaximum Likelihood (Оцінювання методом максимальної правдоподібності) у двох варіан­тах: Approximate(Наближене) або Exact (Точне). При цьому кори­стувач задає настройки (Options), що регулюють ітераційний процес (послідовного наближення): Start vals (Початкові значення (шука­них параметрів)); # iterations(Кількість ітерацій); Convergence (Збіжність (критерій збіжності процедури оцінювання)). За умовчан­ням система використовує стандартні настройки. Надійність резуль­тату тим вища, чим менше виражена нестаціонарність РД.

Для зменшення впливу нестаціонарності РД застосовують різні способи (опції) перетворення змінних. Доступ до них здійснюється через діалогове вікно Times Series Transformations (Перетворен­ня часових рядів), яке містить кілька функціональних груп. У групу Transformations: х = f(x) (Перетворення: х = /(х)) включено:

•       Add a constant (Додати константу) до значень РД;

•       Pover (Піднести до степеня);

•       Invers pover (Піднести до оберненого степеня), тобто добути
корінь;

•       Natural log (Натуральний логарифм), тобто логарифмування

РД;

•    Exponent (Експонента) — виконати експоненційне перетво­
рення;

•       Mean substract (Обчислення середнього) — від значень РД
віднімають середнє арифметичне, обчислене за всіма спостере­
женнями, або значення, задане в полі М;

•       Standardize (Стандартизувати) — від значень РД віднімають
величину М і ділять на S. Якщо вибрано опцію Estimate mean
& std dev. from data (Оцінити середнє та стандартне відхи­
лення за даними), то значення М та S обчислюють як вибіркові
відповідно середнє арифметичне та СКВ РД;

•       Trend subtract (Обчислення тренду) — від РД віднімають
лінійний тренд X(t) = а + bX(t), параметри якого а і b або
задаються користувачем, або оцінюються програмою за МНК;

•       Autocorr (Автокореляція) — лінійне перетворення РД виду
X(t) = X(t) — (а + ЬХ(х)), яке дає можливість занудити автоко-
реляції при якомусь значенні t (задається в полі lag).

Опцію Transformations for spectrum analysis (Перетворен­ня для спектрального аналізу) використовують для підготовки РД до розкладання в ряд Фур'є з метою пошуку прихованих періо-дичностей.

Зв'язки між РД вивчаються за допомогою процедур групи Two-series transformations (Перетворення двох рядів):

•       Difference (Різниця) — обчислення нових значень РД за фор­
мулою X(t) = X(t) — Y(t — х), де х (лаг) задається користу­
вачем;

•       Rezidualizing (Залишковий) — забезпечує обчислення пере­
творення X(t) = X(t) — (а + bX(t — х)), де параметри а і b або
задаються, або оцінюються програмою за МНК — опція Estimate
a and b from data (Оцінити а і b за даними).

Опцію Filtering and other techniques (Фільтрація та інші мето­ди) використовують для перетворення РД одним з таких способів:

•    4253Н Filter (4253H Фильтр) — фільтрація РД за допомогою
Ковзного медіанного згладжування за 3, 4 та 5 періодами (точ­
ками):

—  триточкового "вагового" згладжування КС із "вагами" (Hanning
weights): 0,25; 0,50; 0,25;

—  обчислення залишків;

—  застосування до залишків перетворень 1 та 2;

—  додавання перетворених залишків до перетвореного РД;

•    Diferencing (Диференціювання) — оцінка першої похідної
шляхом обчислення перших різниць за формулою

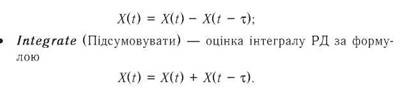
Після виконання процедури оцінювання вирішальним моментом, на наш погляд, є оцінка якості результатів і адекватності моделі. Для цього в системі STATISTICA передбачено групу команд (кнопок) Plot of resuduals (Графіки залишків), що видаються з діалогового вікна Singles Series ARIMA Results(Результати АРІКС РД). З їх допомогою можна:

•       вивести на екран і роздрукувати графік залишків в координа­
тах нормального ЗРЙ (як на нормальному ймовірнісному па­
пері). Прямолінійний вигляд графіка означає, що залишки підпо­
рядковуються нормальному ЗРЙ і аналіз виконано якісно;

•       подати залишки у вигляді гістограми з накладенням на неї
графіка функції нормального ЗРЙ. Близькість графіків свідчить
про повноту вибраної моделі;

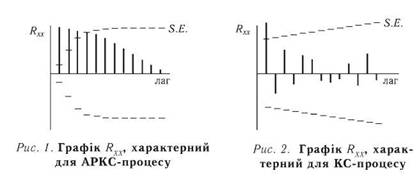
•       вивести графік автокореляційної функції залишків з додаван­
ням таблиці параметрів р, q і стандартної помилки (S.E.). По­
рівняння цих даних дає можливість судити про адекватність
моделі прогнозованого процесу. Наприклад, для АРКС харак­
терне поступове "вимирання" статистично значущих піків R
(рис. 1), а для процесів КС — наявність одиничного піка на
першому лазі (рис. 2).

Для отримання результатів прогнозу використовують набір опцій Forecasting (Прогнозування). У полі Numbers of cases (Кількість

випадків) зазначають кількість часових періодів (кроків), на яку ми хочемо поширити прогноз. У полі Confidence level (Рівень довіри) задають довірчу ймовірність висновку (звичайно 0,95), а в полі Start ofcase (Почати з випадку) — вибирають номер періоду, з якого почи­нають будувати прогноз. Після включення опції Append forecasts to original series on Exit (Додати прогноз у кінець ряду спостережень) на графіку РД виводяться підкреслені пунктиром прогнозовані значен­ня, а штриховими лініями виокремлюється довірчий інтервал прогнозу. Викладене аж ніяк не вичерпує всіх методів ідентифікації моде­лей РД, що забезпечуються системою STATISTICA; ставилася мета продемонструвати принципи роботи з цією програмою. Можливості її значно ширші, а впровадження у практику менеджменту СР може дати неоціненні результати.