3.1. Моделі оптимального розміщення туристичних комплексів на заданій території

1.1. Розглянемо деяку територію Т (наприклад, територію Чернівецької області або іншого регіону), яка є привабливою в плані туристичної індустрії. Будемо вважати, що на території Т розміщені m туристично-рекреаційних об’єктів (ТРО), кожний з яких характеризується певним набором рекреаційних характеристик. Для простоти будемо характеризувати і-ий ТРО тільки одним числом pі - коефіцієнтом рекреаційної привабливості або рекреаційним потенціалом. Величини pі,  можна визначити, наприклад, за допомогою методу експертних оцінок. Щоб з’ясувати місця оптимального (або квазіоптимального) розміщення туристичних комплексів (ТК) на даній території Т, карту (або картографічне зображення) території Т покриємо деяким прямокутником II = [а, b] х [с, d]. У системі декартових координат хОу (тобто у векторному просторі R2) можна прямокутник П визначити так:

Запис , означає, що xо є розв'язком задачі

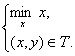
Аналогічний зміст мають і інші записи такого типу.

Очевидно, що прямокутник П містить множину (територію) Т(ТÌП).

Розіб’ємо прямокутник П (а значить і територію Т) сіткою D = Dх х Dy, де

Надалі можна вважати, що hх =hу.

Нехай D(т) Ì D - множина всіх вузлів сітки D, які розміщені на території Т. Пронумеруємо всі вузли сітки D(т) індексами  та позначим через Pj - рекреаційний потенціал j-гo вузла (тобто вузла (xj,yj) ÎD(т) в крузі

(x-xj)2+ (y-yj)2 £ R2,

де R - радіус (в км)).

Величини pj будемо визначати так:

де Іj - множина індексів ТРО, які знаходяться від вузла-центру (xj,yj) на віддалі, яка не перевищує R км.

Стратегія вибору місць розміщення ТК така: туристичні комплект повинні бути розміщені в таких місцях, сумарний рекреаційний потенції і яких є максимальним. Введемо змінні:

якщо для ТК вибрана точка(хj,уj), в іншому випадку;

Тоді модель оптимального розміщення туристичних комплексів на території Т є наступною задачею булевого (дискретного) програмування:

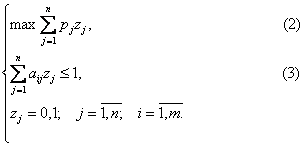
Згідно з розв'язком цієї задачі ТК слід розмістити в точках локальних максимумів рекреаційного потенціала. Доцільність такого вибору підтверджена експертами при вивченні, наприклад, туристичної галузі в Криму [56].

1.2. Задача (2) - (3) є детермінованою задачею. У багатьох випадках є зміст розглядати стохастичні аналоги цієї задачі.

Справді, логічно припускати, що рекреаційні потенціали  виділених на території Т ТРО є випадковими величинами, тобто залежними від стану природи wÎW. Це означатиме, що pі(w),  є функціями від елементарної події деякого імовірнісного простору [21] (W,F,P), де W - множина елементарних подій, F - s-алгебра подій, Р -імовірнісна міра, визначена на W і F.

Зрозуміло, що тоді рекреаційні потенціали Pj, , вузлів сітки D(т) також будуть випадковими величинами:

Якщо М[.] - операція математичного сподівання, то, враховуючи (4), можна написати рівність:

Тоді модель оптимального розміщення ТК на території Т зводиться до задачі стохастичного дискретного програмування (задачі планування за середніми):

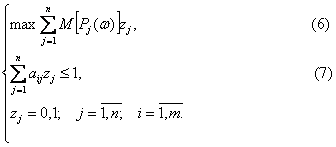
Зауважимо, що у випадку, коли множина складається з скінченого і невеликого числа елементів, то при визначенні оптимального розміщення ТК можна розглянути також модель планування за варіантами [21].

Задача (6) - (7) та їй подібні належать до класу важливих прикладних стохастичних моделей ризику.