3.1.2 Екстраполяція на основі плинної середньої
Метод плинної середньої базується на використанні залежності:
![]()
де n-кількість років "передісторії". Коефіцієнт Лгрозраховується за формулою

|
|
| де і число, яке означає послідовний натуральний ряд “передісторії” , починаючи з останнього; /?- визначається по таблиці, поданій нижче: |
Якщо підставити розраховані значення Яу формулу (3.23), отримаємо:
![]()
Особливістю методу плинної середньої є те, що рівень показників, який знахо-диться ближче до прогнозованого періоду, чинить більший вплив на значення прогнозованих показників, порівняно з віддаленими періодами. Досягається це завдяки коефіцієнту Я.
Прогнозні значення показників розраховуються наступним чином:
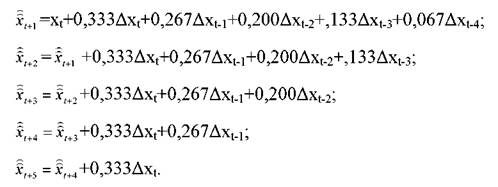
На підставі даних другої п'ятирічки, включаючи також базисний період (табл.3.1) складемо прогноз споживання кондитерських виробів на основі методу плинної середньої. Розрахуємо абсолютні прирости
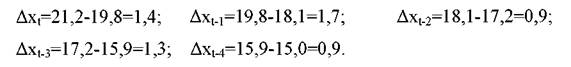
Виходячи з наведених вище залежностей

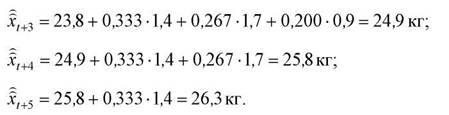
Порівняємо розрахунки прогнозу споживання кондитерських виробів на одну людину по області, що розраховані на основі середньорічного коефіцієнту росту і плинної середньої (табл.3.6)
Таблиця 3.6
Прогноз споживання кондитерських виробів на наступну п'ятирічку, розрахований двома методами, кг.
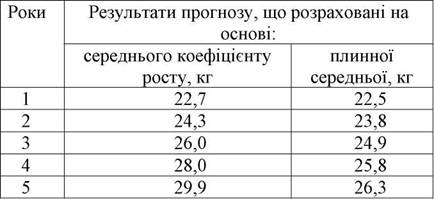
Дані табл. 3.6 свідчать про те, що прогноз, складений на основі середньорічних коефіцієнтів росту, за результатами дещо випереджає прогноз, складений по методу плинної середньої.
Який прогноз виявиться точнішим, зробити висновки заздалегідь важко.
Разом з тим перевага методу плинної середньої є те, що на значення прогнозованих показників впливають в тій чи іншій мірі усі дані "передісторії", в той час, коли значення середньорічного коефіцієнта росту визначається тільки крайніми величинами динамічного ряду.
Наявність альтернативних варіантів прогнозу дозволяє спеціалістам на основі досвіду, знання, інтуіції відібрати найбільш прийнятний.

