3.2. Оптимальна організація функціонування туристично-рекреаційних систем

Однією з найбільш важливих проблем організації туристично-рекреаційної системи є проблема раціонального використання рекреаційних ресурсів, а також максимальне задоволення інтересів ТРC як окремого бізнесового комплексу.

Нехай ТРС складається з т туристично-рекреаційних об’єктів (ТРО) обслуговування, відвідувачі (рекреанти) яких діляться на п типів. Введемо наступні позначення:

х(j)i - чисельність рекреантів j-гo типу в ТРО і;

 = (х (j), ...,х(j)m)' - шуканий вектор числа рекреантів типу j (), розміщених в ТРО обслуговування і ();

A(j) - матриця розміру (m х m), кожний елемент а(j)i'i якої є ймовірність того, що рекреант j-гo типу з ТРО і' переміститься в ТРО і у наступнии період часу;

В(k,j) - матриця розмірності (m х m), кожний елемент якої b(k,j)i'i - цe величина послуг типу k в пункті і', які потрібні відвідувачу j-гo типу який знаходиться в пункті (ТРО) і;

с-(л) = (c1k, ...,cm)' - вектор вмістимості ТРО і для послуг k:-го типу;

К - кількість послуг в ТРС;

d(j)i, - максимальний попит рекреантів j-гo типу на послуги ТРО і.

Тоді модель організації оптимального функціонування ТРС матиме вигляд:

 

 

Легко бачити, що в даній моделі максимізується загальна кількість рекреантів ТРС.

Співвідношення (9) стверджують, що число рекреантів кожного типу в ТРС дорівнює сумі тієї частини, яка залишилась там від попереднього періоду і тих, що прибули з інших пунктів.

Обмеження (10) - це обмеженість на вмістимість рекреантів в залежності від послуг, а (11) - це обмеження на попит.

Як відзначено в [123], для такого типу моделей можна розглянути різні критерії функціонування ТРС.

Зауважимо також, що обмеження моделі (8) - (11) теж можна упростити або доповнити іншими обмеженнями, що дає змогу отримати інші варіанти моделей оптимального функціонування ТРС.

Крім вище вказаної розглянемо наступну модель оптимального функціонування ТРС.

Нехай рекреаційний процес в ТРС як процес відновлення фізичних, інтелектуальних та емоціальних сил людини включає множину К послуг та забезпечується L рекреаційними ресурсами (природними ресурсами).

Позначимо через

Р(k)ij - вартість послуги k для одного рекреанта j-гo типу в ТРО з номером і;

x(k)ij - шукана кількість рекреантів j-гo типу в ТРО з номером і, які користуються послугою k;

Кi - множина послуг, які надаються рекреантам в ТРО з номером і (Кi Ì К);

d(k)ij - максимальний попит рекреантів j-гo типу в ТРО з номером і на послугу k Ì К;

r(k,l)ij  - витрати рекреаційного ресурсу з номером l на послугу k для одного рекреанта j-гo типу в ТРО з номером і;

 - вектор пропозиції рекреаційних ресурсів, які можуть бути використані в рекреаційному процесі даної ТРС.

Очевидно, що власник ТРС буде прагнути максимізувати доход (сумарну вартість) від наданих послуг рекреантам різних категорій при заданих обмеженнях на пропозицію рекреаційних послуг та ресурсів.

Математична модель цієї ситуації матиме вигляд:

 

 

де Z - множина цілих чисел.

У моделі (12) - (16) знаходяться ті чисельні величини рекреантів, які забезпечують власнику ТРС досягнення мети.

У математичному плані задача (12) - (16) є задачею цілочисельного лінійного програмування. На основі моделі (12)-(16) інколи є зміст розглянути інші варіанти моделей. Наприклад, коли немає диференціювання рекреантів на типи, модель (12) - (16) упроститься (зменшиться розмірність задачі).

Як відомо [123], проблема розміщення туристично-рекреаційної системи є однією з принципових проблем оптимального проектування регіональних рекреаційних систем. Через те при аналізі та прийнятті рішень органом чи особою, які уповноважені приймати рішення (назвемо їх ОПР) важливими є моделі оптимального розміщення ТРС.

Опишемо одну із цих моделей. Нехай

т - кількість можливих місць розміщення ТРС в заданому регіоні;

п - кількість центрів попиту (наприклад, населених пунктів) на послуги ТРС;

pij - максимально можливий попит на послуги ТРС з номером і в центрі попиту з номером j;

tij - затрати часу на переміщення одного рекреанта з j-гo центру попиту в і-ту ТРС;

Pj - мінімально можливий попит на рекреаційні послуги в пункті попиту j;

Кi - максимально можлива кількість рекреантів в ТРС з номером i;

xij - шукана кількість рекреантів із j-го центру попиту, яких приваблює і-а ТРС;

dij - максимальний попит рекреантів з центру попиту j на i-ту ТРС.

Тоді можна формалізувати наступну модель:

 

 

У задачі (17)-(21) кожне з обмежень має чіткий реальний зміст. Задача (17)-(21), в загальному випадку є задачею цілочисельного лінійного програмування.

Що стосується обмеження цілочисельності (тобто (21)), то інколи ним можна знехтувати.

У задачі (17)-(21) мінімізуються сумарні затрати часу на переміщення з пунктів попиту на рекреацію в туристично-рекреаційні системи. Звичайно є зміст також мінімізувати сумарні затрати коштів на переміщення. Для цього досить вважати, що tij - це затрати коштів (вартість) перемішення одного рекреанта з центру попиту j в ТРС і ().

Тоді при тих обмеженнях, що і раніше, модель (17)-(21) матиме дещо іншу інтерпретацію.

Однак в обидвох випадках дана модель оптимізує деякі регіональні економічні показники.

Розвиток індустрії туризму залежить головним чином (при наявності ресурсів) від інвестиційної діяльності. Оптимальне вирішення цієї проблеми можливе з допомогою економіко-математичних методів.

Розглянемо задачу оптимального інвестування галузі туризму та рекреації з їх допомогою. Обмежимось регіональною моделлю (термін регіон тут може вживатись як на макро- так і на мікрорівні). Припустимо. що в даному регіоні знаходиться m туристично-рекреаційних систем (або пунктів), причому для кожної з них пропонується певна множина Мi, () проектів розвитку та функціонування.

Інвестування цих проектів здійснюється деяким регіональним центром інвестицій, який акумулює в собі як державні так і приватні інвестиції. Основним завданням цього центру є збереження певних балансових співвідношень між економічними та екологічними показниками регіону, тобто регулювання допустимих обмежень (допустимої інфраструктури) процесу інвестування в регіоні як економіки в цілому, так і галузі туризму та рекреації.

Оцінка ефективності інвестиційного процесу може бути вибрана по різному. Нижче ми розглянемо в ролі даної оцінки сумарний прибуток від вкладених в розвиток рекреаційних систем інвестицій. Введемо позначення:

cij - прибуток від вкладеної одиниці інвестицій в j-ий проект розвитку i-ої ТРС ();

xij - обсяг інвестицій, вкладених в j-ий проект розвитку i-ої ТРС;

I - загальний обсяг інвестицій, які виділяються для розвитку туризму та рекреації даного регіону.

Тоді одна з найпростіших моделей оптимального інвестування галузі туризму та рекреації даного регіону матиме вигляд:

 

 

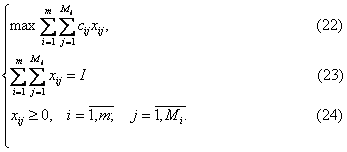
Зробимо три зауваження. По-перше, замість величини прибутку cij (якщо вона є випадковою величиною) слід брати її середньоочікуване значення, тобто математичне сподівання M[cij], що приводить нас до стохастичного аналогу моделі (22)-(24). По-друге, в багатьох випадках нас не стільки цікавить прибуток від вкладених інвестицій, скільки їх корисність (корисність інвестицій xij є деякою функцією kij(xij). По-третє, обмеження (23) в загальному випадку слід змінити на обмеження-нерівність. Однак, методи розв'язування задачі (22)-(24) в обидвох випадках аналогічні. Зупинимось детальніше на задачі (22)-(24).

Вона є задачею лінійного програмування (транспортного типу). Все ж її можна розв’язати методом динамічного програмування [7,18]. Для цього задачу (22)-(24) будемо розглядати як задачу багатоетапної оптимізації (або задачу оптимального керування дискретним процесом зі скінченим числом етапів).

Перейдемо від двохіндексних змінних xij до одноіднексиних и(l), а від сij - до c(l). Тоді задача (22)-(24) зведеться до дослідження ефективності вкладених інвестицій спочатку в один проект, а потім в два проекти і т.д., і накінець - в L проектів.

Отримаємо L станів системи, кожний з яких опишемо обсягом інвестицій х(l) вкладених в перших l проектів. Величину u(l) будемо вважати величиною керування на l-му етапі.

Тоді (22)-(24) зведеться до наступної задачі:

 

 

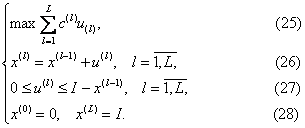
Задача (25)-(28) успішно розв'язується методом динамічного програмування. При реальних конкретних даних можна отримати реальний оптимальний розв'язок. Модель (25)-(28), як і їй подібні, входять в систему моделей оптимального керування економікою регіону [19,20].

Повернемось знову до процесу моделювання оптимального інвестування індустрії туризму та рекреації. Насамперед відзначимо, що з позицій регіону (ОПР) варто накласти певні обмеження (знизу та зверху) на величини хij. Це дасть можливість добитись раціонального інвестування всіх проектів розвитку туризму та рекреації у регіоні в цілому, а отже не порушити інфраструктуру цієї галузі.

Таким чином, доповнимо обмеження (23)-(24) обмеженнями:

де величини x*ij та x**ij повинні бути реально узгоджені із загальним обсягом інвестицій I (x*ji £ x**ij£ І). Крім того, величини x*ij та x**ij можуть бути як заданими так і шуканими.

У довільному випадку отримаємо нову модель оптимального інвестування туристично-рекреаційної діяльності в регіоні - модель (22)-(24), (29).

У моделях (22)-(24) та (22)-(24), (29) можна вважати, що неявно врахований і екологічний фактор, тобто фактор боротьби із забруденням навколишнього середовища в процесі туристично-рекреаційної діяльності та відновлення екосистеми. Запропонуємо інший (надзвичайно простий) варіант моделі оптимального інвестування туризму та рекреації в регіоні з врахуванням екологічного фактору.

Нехай для кожної i-ої ТРС відомі:

ai - доля капіталу, який використовується на розвиток ТРС ();

bi - доля капіталу, який використовується на боротьбу із забрудненням, як наслідком рекреаційної дiяльностi ().

Зрозуміло, що визначення величин ai, bi () - це окрема задача, причому досить складна. Однак, в рамках даної моделі будемо вважати, що ця задача apriori розв’язана. Враховуючи ai, та bi, кожна i-та ТРС може в даний період визначити мінімально допустимий обсяг капіталу Ii, який потрібний для збереження еколого-економічної рівноваги в районі ТРС.

Отже, обмеження (23)-(24) і (29) слід доповнити обмеженнями:

 

 

Звичайно, в реальних моделях обмеження (23)-(24) і (29)-(30) повинні бути узгодженими, тобто допустима множина, яку вони описують, повинна бути не порожньою.

У кінцевому результаті матимемо модель (22)-(24), (29)-(30) - модель оптимального інвестування рекреаційної діяльності в регіоні з врахуванням екологічного фактора.

Одним з важливих економічних показників функціонування довільного туристично-рекреаційного об’єкта (ТРО) як об’єкта, що продукує комплекс послуг, необхідних для задоволення необхідних потреб рекреанта, є рентабельність виробництва послуг.

Побудуємо модель планування максимальної рентабельності в туристично-рекреаційній системі. Позначимо через

т - кількість ТРО, які входять в дану ТРС;

ni - кількість різних послуг, які продукуються в i-му ТРО ();

 - питомі витрати туристично-рекреацшного ресурсу l-го виду на виробництво (чи надання) однієї послуги j-гo виду в і-му ТРО;

L - кількість туристично-рекреаційних ресурсів, за допомогою яких в ТРС продукуються різні послуги;

R(l) - максимальна пропозиція l-го ресурсу;

xij - шукана кількість послуг j - го виду, які продукуються в ТРО і;

pij - вартість однієї послуги j-гo виду в ТРО і;

vij - питомі виробничі витрати (в грошових одиницях) на виробництво однієї послуги j-гo виду в ТРО і;

У прийнятих позначеннях модель планування виробництва послуг в ТРС з максимальною рентабельністю формалізується так:

 

 

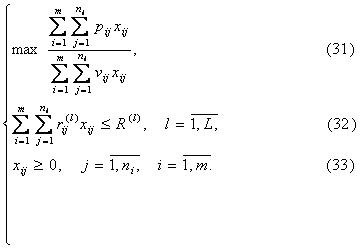
Задача (31)-(33) є задачею дробово-лінійного програмування. Ця задача зводиться до задачі лінійного програмування, тому може бути розв’язана відомими методами [7,18].

Можна також розглянути аналог моделі (31)-(33), в якому всі або деякі змінні хij є цілочисельними. Задача планування виробництва послуг з максимальною рентабельністю в одному ТРО аналогічна до (31) - (33) та співпадає з стандартною задачею дробово-лінійного програмування [7,18].

Заслуговує особливої уваги питання математичного моделювання багатокритеріальних систем, якою власне і є туристично-рекреаційна система.

Порівняно з однокритеріальними моделями, багатокритеріальні моделі відображають внутрішню сутність динамічного процесу розвитку та функціонування ТРС, а також мають, як правило, високий рівень адекватності реальним процесам та системам.

Запропонуємо одну із серії таких моделей. Нехай

xj – об’єм рекреаційного ресурсу j-гo виду, який направляється для продукування послуг в ТРС ();

 - мінімально та максимально допустимі об’єми j-гo ресурсу, які забезпечують нормальне функціонування ТРС.

aj - доля об’єму j-гo ресурсу, який реально використовується в ТРС ((1 -aj) - доля відходів);

сj - прибуток ТРС від реалізації одиниці j-гo ресурсу;

ej - витрати енергії на реалізацію одиниці j-гo ресурсу;

kj - корисність (наприклад, оцінка споживача-рекреанта) від реалізації одиниці j-гo ресурсу;

R - максимальна сумарна ресурсопотужність ТРС.

Тоді матимемо модель:

 

 

Очевидно, задача (34)-(39) є трьохкритеріальною задачею лінійного програмування.

Одним із методів розв'язування такої задачі є її зведення до багатопараметричної задачі лінійного програмування [60], яка полягає в максимізації функції

 

 

при обмеженнях (37)-(39) та обмеженнях вигляду:

 

 

Якщо коефіцієнтам bj () арrіоrі задати конкретні значення, то функція (40) буде конкретною згорткою і задача (34)-(39) зведеться до однокритеріальної задачі.

Однак зупинятись на детальному аналізі цих задач та методів їх розв'язування немає змісту. Зауважимо також, що в більш загальному випадку функції прибутку, корисності та витрат енергії можна вважати нелінійними.

В умовах ринкової економіки, коли існує жорстка конкуренція між об'єктами ринку, до яких, зокрема, належать туристично-рекреаційні системи, однією з важливих проблем є проблема розподілу обмеженого ресурсу. Моделювання процесу розподілу обмеженого ресурсу між користувачами (ТРС) ускладнюється тим, що користувачі не зацікавлені в розповсюдженні інформації про свої доходи.

Крім того, користувачем може бути не тільки окрема ТРС чи регіон, а й окрема країна і ін.

Розглянемо одну з найпростіших моделей такого типу. Нехай

R - наявна кількість обмеженого рекреаційного ресурсу;

п - число ТРС - користувачів між якими здійснюється розподіл даного ресурсу;

xj - кількість ресурсу, яку отримує j-тий користувач;

Pj(xj) - функція доходу j-того користувача.

Модель розподілу обмеженого ресурсу має вигляд:

 

 

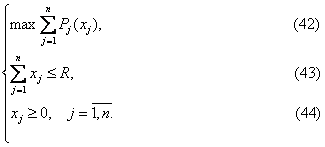
Якщо функції Pj(xj) відомі, то задачу (42)-(44) можна звести до багатоетапної задачі оптимізації (або задачі оптимального керування) і розв’язати відомими методами (наприклад, методом динамічного програмування).

Якщо користувачі не зацікавлені в тому, щоб їх функції Pj(xj),  були відомими, то задачу (42)-(44) не можна розв’язати одним координуючим органом.

В зв’язку з цим були розроблені так звані алгоритми децентралізованого розв'язування даної задачі, які не вимагають обміну інформацією між учасниками - користувачами [60].