3.3. Дослідження попиту та моделювання інтересів окремого рекреанта

Розглянуті вище моделі (наприклад, (12)-(16) або (8)-(11)) відображають інтереси власника ТРС.

Зрозуміло, що актуальною задачею є також вивчення (або моделювання) інтересів (зокрема, економічних) окремого рекреанта. Нехай, як і раніше, ТРС включає в себе m пунктів рекреації (ТРО). Позначимо через J -множину послуг, які надає ТРС в цілому, а через Jі() - множину послуг, які надаються в ТРО і (). Очевидно, Ji Ì J,. Будемо вважати, що деякий потенційний рекреант має намір брати участь в рекреаційному процесі даної ТРС. Вивчимо поведінку рекреанта з позицій його інтересів.

Приймемо позначення:

si - деяка середньоочікувана вартість переміщення рекреанта від місця знаходження М до пункту рекреації і ();

di'i - середньочікувана вартість переміщення рекреанта між рекреаційними пунктами і' та і (можна вважати, що dii = 0, , a di'i=dii' i', , i'¹ i

ciji. - середньоочікувана вартість послуги ji, Î Ji в пункті і;

Рі - середньоочікувана вартість переміщення рекреанта з пункту і в пункт М після завершення рекреаційного процесу (часто Pi, та si, можуть співпадати);

Далі припустимо, що рекреанту потрібен набір N Ì J кількістю n послуг, які є в даній ТРС (тобто в множині J), але повного набору послуг N немає в кожному окремому ТРО з номером і(). Така ситуація є цілком реалістичною і не потребує окремих обгрунтувань. В цьому випадку рекреант вимушений користуватись деякою підмножиною пунктів рекреації, які є в даній ТРС.

Якщо брати до уваги економічний критерій, то стратегічна поведінка рекреанта полягає в тому, щоб мінімізувати сумарну вартість рекреаційного процесу та вартість переміщення його з пункту М в ТРС та назад з ТРС в пункт М.

Враховуючи прийняті вище позначення , цю вартість (середньоочікувану) можна виразити так:

Математична модель, яка реалізує пошук оптимальної стратегії рекреанта, має вигляд:

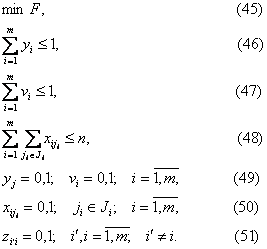
Задача (45)-(51) є задачею булевого програмування.

Обмеження (46) в цій задачі стверджує, що рекреант переміщується з пункту М в один з пунктів рекреації.

Аналогічно (47) - це обмеження: рекреант повертається в пункт М з одного з пунктів рекреації.

Зміст обмеження (48) наступний: для рекреанта кожна послуга j Î N задовольняється тільки в одному з пунктів рекреації.

Обмеження (49)-(51) - це обмеження на дискретність шуканих змінних.

Зауважимо також, що обмеження (46)-(48) можна замінити на обмеження - рівності. Інколи є зміст розглянути інші аналоги моделі (45) - (51).

Актуальним для окремого рекреанта є також раціональний (оптимальний) розподіл фінансових ресурсів (наприклад, грошей) на послуги, які можуть надаватись рекреанту в даному пункті рекреації (тобто ТРО).

Нехай

s - максимальний обсяг фінансових ресурсів, які рекреант може виділити на задоволення послуг рекреаційного процесу;

п - кількість послуг в даному рекреаційному пункті;

ci - вартість однієї послуги i-го виду ();

хi, - шукане число послуг i-го виду, якими користується рекреант;

ki - корисність однієї i-тої послуги (це може бути деякий ваговий коефіцієнт, яким оцінюється значущість i-тої послуги або в більш загальному випадку - значення деякої функції корисності рекреанта).

Тоді розумна поведінка рекреанта полягатиме в тому, щоб при заданих фінансових обмеженнях максимізувати сумарну корисність свого рекреаційного процесу.

Модель такої поведінки має вигляд:

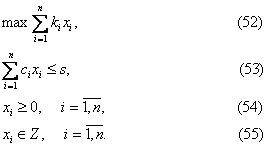
Інколи обмеження на цілочисельність можна зняти (або частково зняти, коли допустима цілочисельність тільки окремих змінних).

Величини kі можна також замінити їх математичними сподіваннями і розглядати стохастичний аналог моделі (52)-(55).

Зауважимо, що можна побудувати багато інших моделей, які описують оптимальну поведінку окремого рекреанта, однак зупинятись на цьому в рамках даної праці ми не будемо.