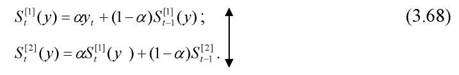3.3.2. Розрахункові формули
Розрахункові формули розглянем для двох випадків: часовий тренд описується лінійним рівнянням; часовий тренд описується квадратичним рівнянням.
|
|
| Експоненціальні середні розраховуються за формулами |
|
|
Лінійне рівняння
Оскільки згідно з формулами (3.68) неможливо розрахувати S\l_\ і 5^ при
t=1, то для 1-го елемента, тобто t=1, визначаються початкові умови за формулами
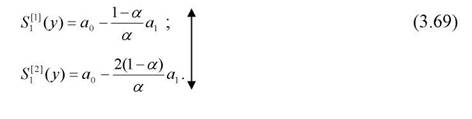
В формулах (3.69) a0 і a1 відповідають коефіцієнтам рівняння часового
тренду, що був одержаний методом найменших квадратів.
Щоб виразити коефіцієнти рівнянь тренду (3.67) через експоненціальні середні, використовується система рівнянь, що пов'язує оцінки коефіціентів
a0 іa1 з названими експоненціальними середніми
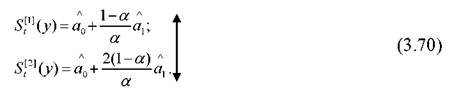
Реалізувавши систему рівнянь відносно a0 іa1, отримаємо:

Прогноз розраховується за формулою

де р- величина горизонту прогнозу.
Помилка прогнозу розраховується за такою формулою:
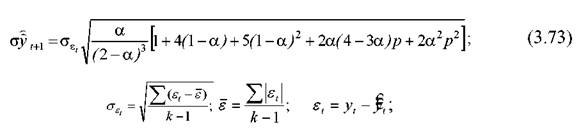
Інтервал довіри визначається таким чином: • для "передісторії"
![]()
де yt - інтервал довіри - верхній(нижній) в t-ому періоді; yt - розрахункове значення показника в t-ому періоді;
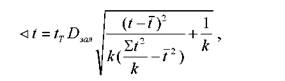
де tT - табличне значення t-критерію Ст'юдента.
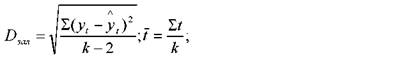
• для прогнозу
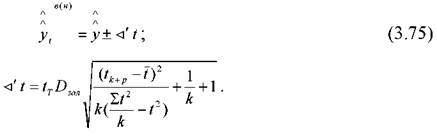
Квадратичне рівняння

Експоненціальні середні визначаються за формулами
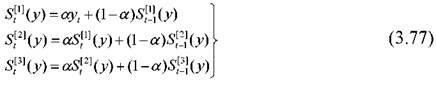
Початкові умови визначаються за формулами
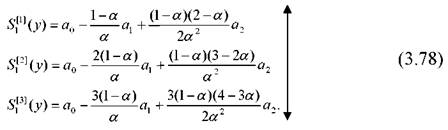
Л Л Л
Як і для лінійного рівняння коефіцієнти a0,a1,a2 відповідають параметрам рівняння (3.76) і визначаються за допомогою методу найменших квадратів.
Л Л Л
Для зв'язку коефіцієнтів a0,a1,a2 з експоненціальними середніми використовується система рівнянь
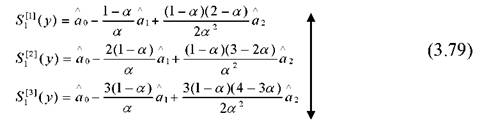
Л Л Л
Розв'язавши систему рівнянь (3.79) відносно a 0, a 1, a 2, одержимо
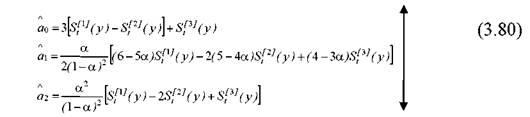
Прогноз розраховується за формулою

Помилка прогнозу визначається за формулою
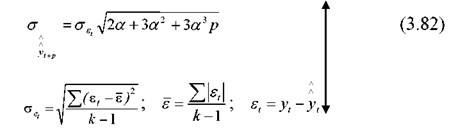
Інтервал довіри для квадратичного рівняння визначається таким чином, що і для лінійного, тобто за формулами (3.74, 3.75).
При побудові прогнозу методом експоненціального згладжування однією з проблем є вибір оптимального значення параметра згладжування а.
Точного методу для вибору величини а на даний момент не відомо. Автор методу експоненціального згладжування англійський вчений Р.Г.Браун рекомендує таку формулу для розрахунку а.

де m - число рівнів, що входять в інтервал прогнозування.
2 Для прогнозу на п'ять років а =2= 0,33 . Це число у більшості випадках
округлюється до 0,35.
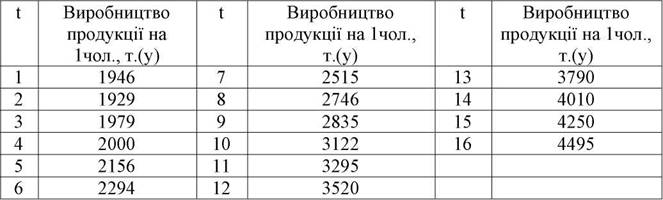
Для ілюстрації використання методу експоненціального згладжування в прогнозуванні для прикладу використаєм дані, подані в табл. 3.15.
Перед тим, як проводити експоненціальне згладжування, необхідно перевірити, яким рівнянням - лінійним чи квадратичним краще описується тенденція змін динамічного ряду. Виходячи з методу "прогноз екс-пост", всі
раніше зроблені розрахунки будуть проводитись на основі даних за 11 років (t=l-e-k); прогноз - на основі даних t=12-=-n (k=1 1; n=16; p=n-k= 16-11=5).
Таблиця 3.15 Виробництво продукції на одного працівника
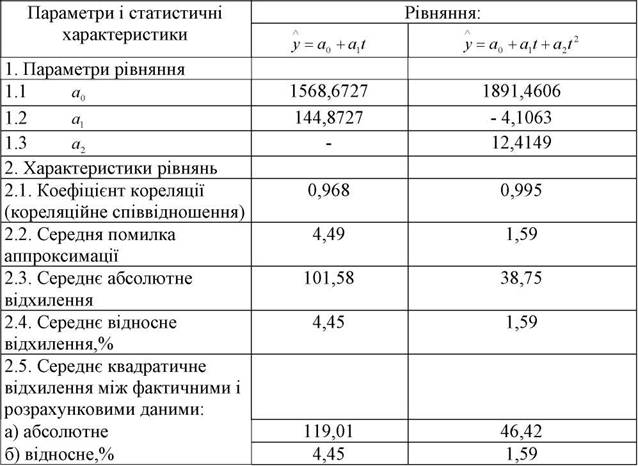
В табл.3.16 наведені значення параметрів і статистичних харатеристик рівнянь, отриманих на основі реалізації методу найменших квадратів і розрахунків за відповідними формулами (3.42; 3.43; 3.45; 3.46; 3.47; 3.48).
Таблиця 3.16 Параметри і статистичні характеристики рівнянь
|
|
Порівняння статистичних характеристик свідчить про те, що квадратичне рівняння більш адекватно відображає процес ніж лінійне.
В практичних розрахунках всі обчислення слід вести по квадратичному рівнянню. Однак для наочності і аналізу результати розрахунків будуть представлені як для квадратичного, так і для лінійного рівняння.
Оскільки прогноз буде проводитись на п'ять років, то от =0,35.
Л
Лінійне рівняння y = a0 +a1t.
На основі формули (3.69) обчислимо початкові умови
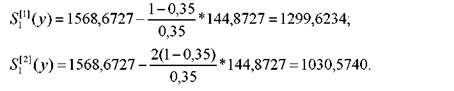
У відповідності з формулою (3.66) обчислимо експоненціальні середні для всіх t=2-=-ll


Згладжений вирівняний динамічний ряд в "передісторії", отриманий за допомогою експоненціального згладжування, обчислюється за формулою (3.72) при р=1таt = 2ч-&.
При побудові прогнозу за формулою (3.72) значення а0 тaa. a j приймається за рівнем t=k і постійні для всього горизонту прогнозу (к+1; k+2; k+3 і т.д).
Отже, в формулі змінюється тільки величина р, яка приймає послідовно значення 1;2;3;4 і т.д. в залежності від величини горизонту прогнозу. Звідси, за формулою (3.72), прогнозні значення дорівнюють:
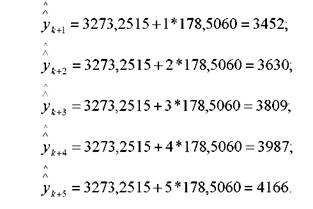
Значення a0 та a1 для t = k = 11 містяться в табл. 3.17
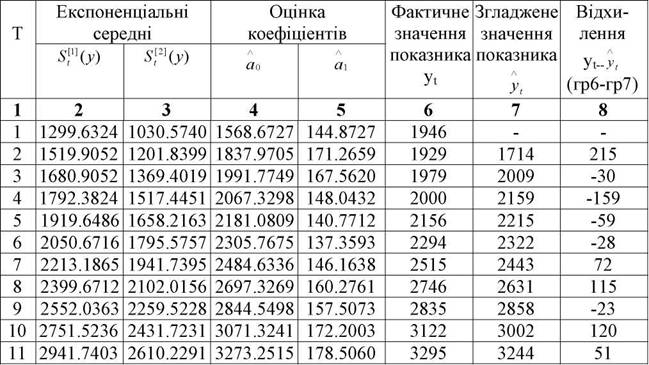
В табл. 3.17; 3.18; 3.19 наведені результати розрахунків за допомогою методу експоненціального згладжування на основі лінійного рівняння
Таблиця 3.17 Послідовне вирівнювання даних "передісторії" динамічного ряду за
Л
методом експоненціального згладжування на основі рівняння y = a0 + a1t
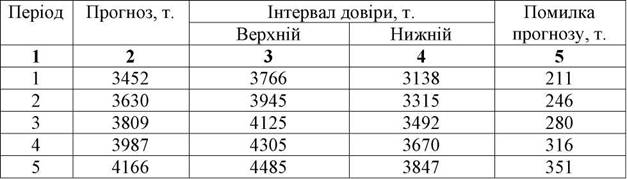
Таблиця 3.18
Прогноз виробітку продукції на одного працівника за методом експоненціального згладжування
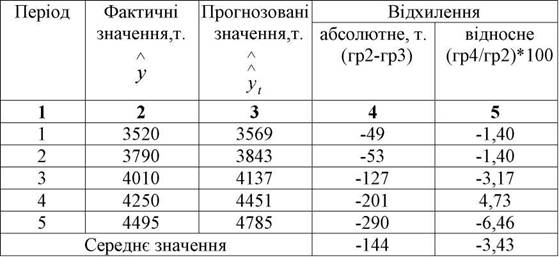
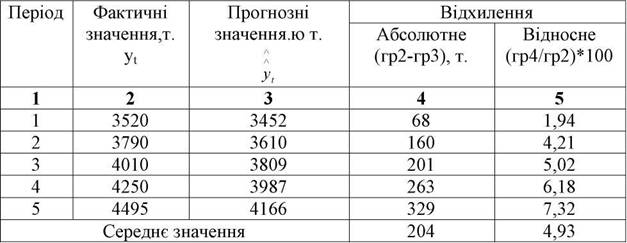
Таблиця 3.19 Порівняння фактичних даних з прогнозованими значеннями
Квадратичне рівняння y = a0+a1t + a2t2.
Всі розрахунки для квадратичного рівняння, особливо розрахунки початкових умов, експоненціальних середніх, коефіцієнтів а 0, а і, а 2 та ін. здійснюються за встановленими формулами і в тій же послідовності, що і для лінійного рівняння.
За формулою (3.78) розрахуємо початкові умови:
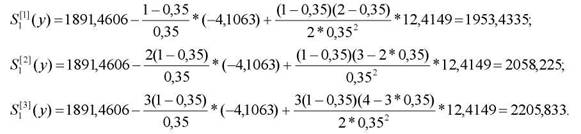
Експоненціальні середні за період t=2-=-l 1 знайдемо за формулою (3.77)

Аналітично, як і для лінійного рівняння нагадаємо, що згладжений (вирівняний) динамічний ряд в "передісторії", отриманий за допомогою експоненціального згладжування, розраховується за формулою (3.81) прир=1, at=2-k.
При побудові прогнозу виконуються ті ж самі правила, що і для лінійного
рівняння, тобто в формулі (3.81) значення a0,a1,a2 приймаються за рівнем t=k-=-ll і постійні для всього періоду (k+1; k+2; k+3; і т.д.) В формулі (3.81) змінюється тільки величинаp, яка послідовно приймає значення 1; 2; 3 і т.д. в залежності від горизонту прогнозування.
Результати розрахунків за методом єкспоненціального згладжування на основі квадратичного рівняння наведені в табл. 3.20; 3.21; 3.22.
Таблиця 3.20
Послідовність вирівнювання даних "передісторії" динамічного ряду за методом експоненціального згладжування на основі рівняння
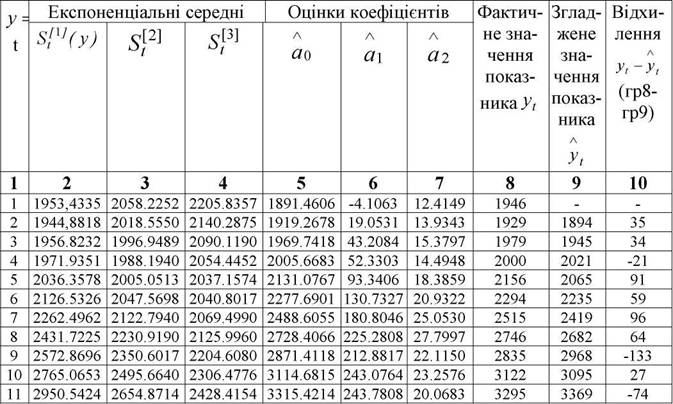
Таблиця 3.21 Прогноз виробітку продукції на одного працюючого за методом
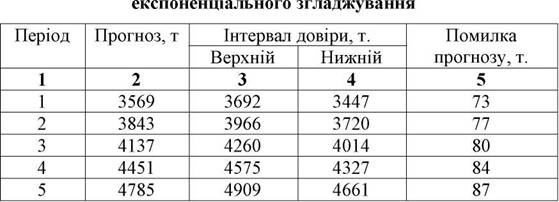
Таблиця 3.22
Порівняння фактичних даних з прогнозованими значеннями
|
|
Наявність параметрів лінійного і квадратичного рівнянь, що розраховуються для визначення початкових умов (див. табл. 3.16), дозволяє застосовувати їх для побудови прогнозу на основі використання часового тренда. В табл.3.23 дані оцінки результатів такого прогнозу.
Таблиця 3.23
Порівняння фактичних і прогнозних значень, розрахованих на основі часового тренда
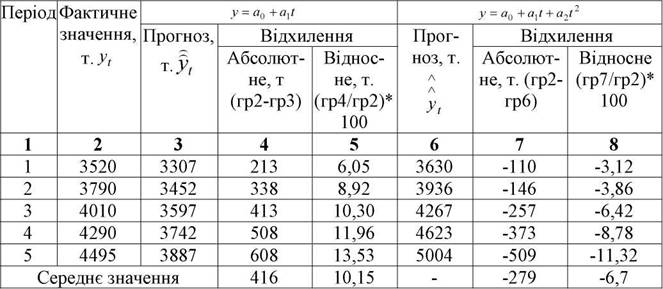
За даними табл.3.19; 3.22; 3.23. проведемо порівняльну оцінку всіх варіантів прогнозу з використанням відносного відхилення фактичних значень показника від прогнозованих значень (табл.3.24)
Таблиця 3.24
Порівняльна оцінка варіантів прогнозу на підставі відносних відхилень між фактичними і прогнозованими значеннями досліджуваного показника
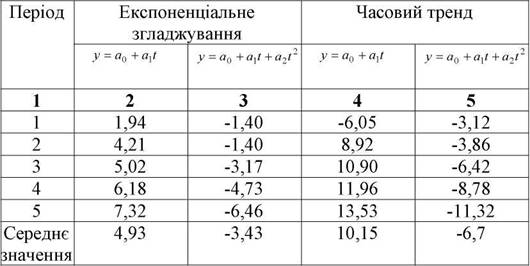
Аналіз даних табл.3.24 свідчить про те, що метод експоненціального згладжування забезпечує значно більш високу (в два рази) точність прогнозу, у порівнянні з прогнозом, що був побудований на основі часового тренду.
Як і слід було очікувати зі значень статистичних характеристик (табл.3.16), використання квадратичного рівняння сприяє отриманню прогнозу більш якісного як в одному, так і в іншому випадку, тобто обома методами.
Разом з тим не можна однозначно вважати, що у всіх випадках метод експоненціального згладжування має переваги перед трендом.