4.2. Логічні основи понятійного мислення
4.2. Логічні основи понятійного мислення
Поняття — це форма мислення, яка відображає предмети в їхніх загальних та істотних ознаках. Ознаками один предмет відрізняється від іншого. Кожна істотна ознака є необхідною, а сукупність істотних ознак є достатньою умовою суттєвого визначення поняття. Воно виражається словом, словосполученням або називним реченням. Слово є звуковим або графічним феноменом, за яким закріплені відповідне предметне значення і смисл. У поняттях відображаються лише загальні та істотні ознаки, а слово має презентувати предмет з будь-якими його ознаками. Слова, які вживаються для відображення думок, повинні мати ясний зміст і чітке значення. Для уникнення розбіжності у тлумаченні значення слова кожна наука створює свою термінологію.
Термін — це слово або група слів, які позначають один-єдиний предмет чи певну групу предметів і вживаються у даній науці з одним чітко визначеним значенням і відповідним змістом. Сукупність термінів, які вживаються у тій чи іншій науці, становить її термінологію.
У сучасній логіці існує теорія імен. Логіку в цій теорії цікавить питання про зв’язок імен з предметами, які ними позначаються, про співвідношення смислу імені та змісту поняття, залежність логічного значення висловлювання від значення імені тощо. Ім’я — це нелогічний термін, який позначає будь-який предмет або клас предметів. При цьому під предметом розуміють усе те, що може бути об’єктом думок (речі, явища, процеси, властивості та відношення як реальних, так і уявних предметів, які або поки що не існують, або у принципі не можуть існувати). Між іменем і його значенням існує відношення іменування, тобто ім’я називає свій денотат (від лат. denatatus — позначений, визначений — те, що можна назвати певним іменем).
Необхідно, щоб відношення іменування відповідало певним принципам: однозначності (ім’я повинне мати лише один денотат, тобто позначати один предмет чи клас предметів); предметності (зв’язки та відношення, які виражає складне ім’я, є зв’язками та відношеннями не між іменами-складниками, а між предметами, які позначаються простими іменами, що входять до цього складного імені); взаємозамінюваності (якщо два імені мають те ж саме предметне значення, то будь-яке з них можна замінити другим, при цьому висловлювання не змінить свого істиннісного значення).
За змістом поняття поділяються на реєструючі та нереєструючі. Основою цього поділу є наявність або відсутність у побічній частині змісту поняття таких ознак, які відповідають на запитання: «де ?», «коли?», «якого роду індивідуум?». Якщо у змісті поняття є ознаки, що відповідають на ці запитання, то вони називаються реєструючими, а в зворотному випадку — нереєструючими. Останні визначаються лише якісно: в них немає ознак, які виділяють у класі предметів певну якісну означеність будь-якої її частини шляхом фіксування просторових або часових меж чи шляхом посилання на одиничність предмета. Тому ці поняття ще називають відкритими, на відміну від закритих (реєстраційних) понять. Приклади нереєстраційних (відкритих) понять: людство, квіти, відданість тощо. Приклади реєструючих (замкнутих) понять: мешканці Києва, студент КНЕУ, Карпатські гори тощо.
Пусті й непусті поняття. Пустими називають поняття, яким не відповідає жоден предмет у предметній області (наприклад, числа N > 2 та N < 3 в області «цілі числа»). Непустими називають поняття, яким відповідають певні предмети в предметній області (наприклад, числа N > 2 i N < 3 в області «раціональні числа»).
Конкретні й абстрактні поняття: перші з них — це поняття про конкретні предмети (машина, людина, тварина, підприємець тощо), а другі — про властивості й відношення предметів (мужність, хоробрість, світлість, мудрість, підприємливість тощо).
Абсолютні й відносні поняття: перші з них виражають повний, незалежний від інших предметів зміст (наука, культура, мистецтво тощо), а другі фіксують відношення одного предмета до іншого (дружина, вчитель, учень тощо).
Позитивні й негативні поняття. Позитивні поняття є результатом узагальнення наявних ознак, а негативні поняття є результатом узагальнення відсутніх ознак предметів. Обидва поняття мають одну родову ознаку, розрізняються за видовою ознакою. За сутністю відношень ці поняття суперечливі (студенти — не студенти, ринок — не ринок, прибуток — не прибуток тощо).
Загальні й одиничні поняття. В загальному понятті мислиться два чи більше предметів (підприємство, ВНЗ, банк тощо). В одиничних поняттях мислиться тільки один предмет (ЗАТ «Арсенал», КНЕУ, АКБ «Надра» тощо).
Безвідносні й співвідносні поняття. Безвідносні поняття відображають предмет, з існуванням якого не пов’язується необхідне існування будь-яких інших предметів (майдан, закон, дерево тощо). Співвідносне поняття відображає предмети, існування яких немислиме без деяких інших предметів (мати, вчитель, староста тощо).
Зміст поняття складають всі його елементи, які можуть бути виділені у вигляді окремих понять. Зміст поняття певною мірою збігається з його визначенням. У ньому можуть мислитися або ознаки однієї категорії речей, явищ дійсності, або ознаки предметів інших категорій, наприклад, категорій речі, властивості, відношення, часу, простору і т.д. Обсяг поняття — це всі інші поняття, для яких воно служить ознакою, головною їхньою частиною. Якщо «А» — це людина, то обсяг цього поняття можна позначити символами Аа (росіянин), Ав (українець), Ас (англієць) і т. д.
Зміст і обсяг поняття регулюються законом оберненого відношення: чим ширше зміст поняття, тим вужче його обсяг, і навпаки — чим ширше зміст поняття, тим вужче його обсяг. Якщо зміст поняття А міститься в змісті поняття В, то це останнє поняття міститься в обсязі першого, і навпаки — якщо поняття В міститься в обсязі поняття А, то останнє становить частину змісту першого. Тобто зміст поняття дає уявлення про його смислове значення, а обсяг — про його предметне значення. У цьому суть закону оберненого відношення між обсягом і змістом поняття.
У відношеннях між поняттями за обсягом насамперед розрізняють порівнянні та непорівнянні поняття. Порівнянними називаються поняття, що мають якісь спільні ознаки, що дають можливість зіставляти ці поняття (табл. 13). Наприклад, «менеджмент» і «маркетинг». Названі поняття належать до того ж самого роду діяльності — управління. Непорівнянними називаються поняття, які не мають спільних ознак, а тому порівнювати такі поняття неможливо. Наприклад, «банк» і «тролейбус». У порівнянних поняттях обсяги повністю або частково збігаються, а в непорівнянних обсяги не мають жодної спільної ознаки. Звідси випливає, що в логічних відношеннях можуть перебувати тільки порівнянні поняття. Порівнянні поняття бувають сумісними або несумісними (табл. 13).
Таблиця 13
ВІДНОШЕННЯ МІЖ ПОНЯТТЯМИ ЗА ОБСЯГОМ
| Порівнянні поняття | |||||
| Сумісні поняття | Несумісні поняття | ||||
|
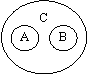
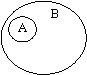
А — Визначення В — Дефініція | Відношення співпідпорядкування А — Спостереження В — Експеримент С — Емпіричні методи | ||||
|
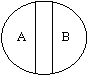
А — Термін судження В — Предикат | Відношення протилежності А — Догматизм В — Релятивізм | ||||
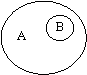
| A B А — Економіст В — Науковець | Відношення суперечності А — Логічний В — Алогічний | ||||
Сумісними називаються поняття, обсяги яких повністю або частково збігаються. Існує три види відношень за сумісністю: рівнозначність (тотожність), перетин (перехресність, частковий збіг обсягів) і підпорядкування (субординація). Несумісними називаються поняття, обсяги яких не мають жодного спільного елемента. Існує три типи відношень між несумісними поняттями: співпідпорядкування (обсяги таких понять включаються до обсягу родового поняття, є його різними видами), протилежності (обсяги таких понять виключають один одного), суперечності (обсяги таких понять повністю вичерпують обсяг родового для них поняття, а зміст одного з них заперечує зміст другого).
Над поняттями та класами понять можна виконувати певні операції, деякі з яких нагадують математичні дії. Сутність операції додавання понять полягає в об’єднанні двох або кількох множин, що становлять обсяги вихідних понять в одну множину. Головна вимога до результату додавання — не допустити «подвійного рахунку» елементів додавання, що збігаються (вони враховуються лише один раз), тобто сума повинна складатися тільки з різних складових обсягу обох понять. Сутність операції множення понять полягає в утворенні нового поняття, обсягом якого є елементи, загальні для вихідних понять. Сутність операції віднімання понять полягає в тому, що утворюється нове поняття, елементи якого не входять до поняття, яке віднімається.
Сутність операції доповнення обсягів понять полягає у запереченні вихідного поняття А шляхом утворення нового поняття А1 (не-А), обсяг якого в сумі з обсягом поняття А становить цілісність, яка дорівнює одиниці: А + А1 =1. Цю базову формулу можна трансформувати у формулу доповнення: А1 = 1 - А.
Наприклад, якщо 1 — економічний вуз, А — КНЕУ, то А1 = = 1 - А (всі інші економічні вузи, крім КНЕУ: КНТЕУ, НАУ тощо).
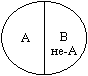
Логічна операція, що розкриває обсяг поняття, називається поділом поняття. Поняття, обсяг якого розкривається, називається діленим поняттям. Ознака, за якою здійснюється поділ, називається основою поділу, а поняття, одержані внаслідок поділу, — членами поділу. Залежно від кількості членів поділу розрізняють поділ двочленний і багаточленний. Серед двочленного поділу виділяють дихотомію (від грец. dιγοτομία — поділ на дві частини), що являє собою поділ обсягу поділеного поняття А на два суперечних поняття — В і не-В. Багаточленний поділ здійснюється за видотворною ознакою, тобто подумки поняття розбивають на види з урахуванням специфіки прояву певної ознаки в різних групах елементів його обсягу. Поділ може бути також змішаним, тобто частково зробленим за правилом дихотомії, а частково — за видотворною ознакою.
Особливим видом поділу є класифікація. Від звичайного поділу класифікація відрізняється тим, що в ній поділ здійснюється за істотною, корінною ознакою, а члени поділу посідають постійне й чітко фіксоване місце. Прикладом класифікації може служити періодична система хімічних елементів Менделєєва. При класифікації можуть бути використані одночасно дихотомія і поділ за видотворною ознакою. Якщо є, наприклад, завдання класифікувати дисципліни, що читаються на будь-якому факультеті, то на першому етапі доцільно зробити дихотомічний поділ предметів вивчення на спеціальні та неспеціальні, а на другому етапі ці дві складові ще раз поділити за видотворною ознакою. Тоді до спеціальних дисциплін, наприклад на юридичному факультеті, будуть зараховані: історія держави і права, теорія держави і права, конституційне право, господарське право, міжнародне право тощо. А до неспеціальних дисциплін на тому самому факультеті будуть включені: логіка, політологія, філософія, інформатика, іноземна мова тощо.
Узагальнення поняття — логічна операція, що полягає в переході від поняття з меншим обсягом до поняття з більшим обсягом. Наприклад: КНЕУ® Вищий навчальний заклад ® Навчальний заклад. Узагальнювати поняття можна до категорій — понять з гранично широким обсягом. Формула узагальнення: Aab ®Aa ®A.
Обмеження поняття — логічна операція, в процесі якої переходять від понять з більшим обсягом до понять з меншим обсягом. Наприклад: Навчальний заклад ® Виший навчальний заклад ®КНЕУ. Обмежувати поняття можна до індивідуальних (одиничних) понять, бо далі буде вже не обмеження, а розчленування цілого на частини, оскільки обсяг понять складається лише з одного елемента. Формула обмеження: A ®Aa ®Aab.
Визначенням поняття, або дефініцією, називається логічна операція, що розкриває зміст поняття. Наприклад: «Холдингова компанія — це компанія, яка володіє контрольними пакетами акцій інших компаній». Поняття, зміст якого визначається, називається визначуваним поняттям (від. лат. definiendum, скорочено — Dfd, те, що визначається); поняття, за допомогою якого розкривається зміст визначуваного поняття, називається визначаючим поняттям (від лат. definience, скорочено — Dfn, те, що визначає).
Логіка пропонує декілька видів визначень (табл. 14).
Таблиця 14
ТАБЛИЦЯ ОСНОВНИХ ВИДІВ
ВИЗНАЧЕННЯ ПОНЯТЬ
| Основні види визначень | |||||
| Явні визначення | Неявні визначення | ||||
| Атрибутивні | Генетичні | Операційні | Контекстуальні | Остенсивні | Аксіоматичні |
Явні визначення задаються конструкцією Р є Q, де Р — дефінієндум, а Q — дефінієнс. Вирізняють три види таких визначень: по-перше, це атрибутивні визначення, в яких видовою ознакою є властивість предмета, що визначається («Афоризм — це короткий влучний оригінальний вислів, що зробився усталеним»); по-друге, це генетичні визначення, в яких видовою ознакою є спосіб походження, створення, конструювання предметів («Гібрид — це статеве потомство від схрещування двох організмів з різною спадковістю»); по-третє, це операційні визначення, в яких є вказівка на операцію, що допомагає розпізнати ті чи інші предмети («Бісектриса — пряма лінія, що проходить через вершину кута і ділить його на дві однакові частини»).
До основних правил явних визначень належать: співмірності (за обсягом Dfd = Dfn); заборони тавтологій (Dfd i Dfn не можна виражати однаковими словами); однозначності (Dfn повинне бути чітким, ясним, неметафоричним, небагатозначним); несуперечності (не можна визначати Dfd через відсутність у нього певних ознак).
Неявні визначення передають смисл терміна через систему його відношень до інших термінів у певному контексті. По-перше, це контекстуальні визначення, в яких контекстом виступає звичайний уривок якого-небудь тексту («Мистецтво довговічне, а життя людини коротке»). По-друге, це остенсивні визначення, які здійснюються за допомогою демонстрації предмета («Ця книга є навчальним посібником з методології соціально-економічного пізнання»). По-третє, це аксіоматичні визначення, в яких контекстом виступає сукупність аксіом даної теорії («Геометрія Евкліда виходить з того, що паралельні лінії ніде й ніколи не перетинаються»).
Існують також номінальні й реальні визначення. Якщо у визначенні розкривається тільки назва поняття, то воно називається номінальним. Якщо ж у визначенні розкриваються істотні ознаки предмета, то воно називається реальним.