4.2.4. Розрахунок параметрів і характеристик моделі.
Параметри рівнянь (а0, аі) розраховуються методом найменших квадратів , який передбачає мінімізацію суми квадратів відхилень між фактичними і розрахунковими значеннями функції (див. формулу 3.38)
Для визначення параметрів складається і реалізується система нормальних рівнянь.
Система нормальних рівнянь для парних моделей складається аналогічно як і для рівнянь тренда (див. 3.40; 3.41).
Система нормальних рівнянь для багатофакторних рівнянь має наступний вигляд: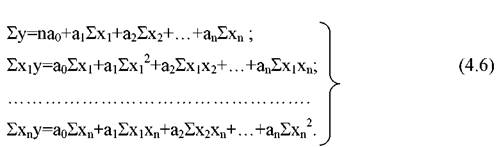
Логарифмічні і степеневі моделі слід спочатку перетворити у лінійні рівняння . Для цього степенева модель перетворюється у логарифмічну шляхом логарифмування лівої і правої частин моделі, а потім, умовно позначивши ln y=u, a ln xi=vi, отримаємо лінійне рівняння
![]()
У лінійних рівняннях (4.3) коефіцієнти при невідомих (аі), які називають коефіцієнтами регресії, відображають співвідношення між кожним фактором і
досліджуваним показником у абсолютних величинах, тобто показують, на скільки одиниць зміниться досліджуваний показник (функція) із зміною певного фактора на одну одиницю при фіксованому (середньому ) значенні решти факторів.
Оскільки функція і фактори частіше всього оцінюються у різних одиницях виміру, то для усунення різнорозмірності і оцінки співвідношення між кожним фактором і досліджуваним показником за допомогою відносних величин, визначається коефіцієнт еластичності. Останній показує, на скільки процентів зміниться функція зі зміною певного фактора на 1% при фіксованому (середньому) значенні інших факторів.
Коефіцієнт еластичності розраховується за формулою

Для лінійних багатофакторних моделей коефіцієнт еластичності дорівнює
![]()
У парних лінійних моделях коефіцієнт еластичності розраховується як середня величина з коефіцієнтів еластичності по кожному значенню фактора
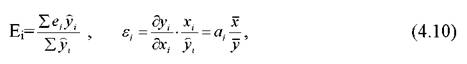
хоча не буде особливої помилки при обчисленні коефіцієнта еластичності у парній моделі за формулою (4.9)
У степеневих і логарифмічних моделях (4.4; 4.5) параметри рівняння (аі) є по суті коефіцієнтами еластичності, тобто Еі=аі.
Дійсно, використавши залежність (4.8), розрахуємо для степеневого рівняння (4.4) коефіцієнт еластичності як приклад для першого фактора:
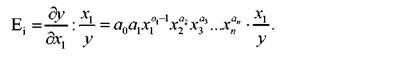
Оскільки як де"1"1 • x1 = х" і замінивши знаменник (у) на його значення (див. модель 4.4), отримаємо
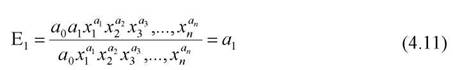
Логарифмічна модель випливає з степеневої , тому названі висновки вірні і для неї.
Абсолютний вплив окремих факторів на рівень результативного показника у степеневих і логарифмічних моделях розраховується за формулою:

Зазначений показник носить назву "додатковий продукт", "гранична продуктивність", "гранична віддача".
Оскільки кожний фактор по своєму впливає на рівень досліджуваного показника, то між взаємозамінними факторами існують певні співвідношення, які дозволяють змінити значення результативного показника (функцію) на одну і ту ж величину.
Зазначені співвідношення, які називаються "граничними нормами заміщення", розраховуються як зворотне співвідношення "граничних продуктів" зі знаком мінус
Одне із понять, яке використовується при аналізі деяких моделей, є рівняння ізокванти.
Рівняння ізокванти застосовується для обчислення значення одного із факторів при фіксованому значенні функції і решти факторів.
Якщо, наприклад, є модель
![]()
то рівняння ізокванти для фактора х1 дорівнює
![]()
Статистична адекватність економіко-статистичних моделей визначається за допомогою ряду статистичних показників. Найбільш суттєвою оцінкою
кожної моделі є встановлення тісноти зв'язку між фактором (або факторами) і досліджуваним показником.
Показниками тісноти зв'язку є: для парної лінійної моделі - коефіцієнт парної лінійної кореляції; для множинної лінійної моделі - коефіцієнт множинної кореляції; для нелінійних моделей (парних і багатофакторних ) -кореляційне відношення.
Коефіцієнт парної кореляції для лінійної моделі розраховується аналогічно формулі (3.42), тобто:
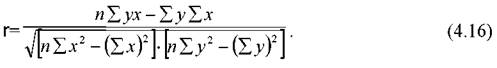
Коефіцієнт множинної кореляції (R) і кореляційне відношення - для множинних і парних нелінійних моделей (г/) розраховуються за формулою (3.43), тобто:
Показники тісноти зв'язку можуть змінюватися в таких інтервалах:

Границі для оцінки тісноти зв'язку подані у формулі (3.44) Коефіцієнт множинної кореляції або множинне кореляційне відношення у квадраті (R2 , if) називається коефіцієнтом детермінації. Останній відображає частку впливу відібраних факторів на величину результативного показника.
Показники: середня помилка апроксимації; середнє квадратичне відхилення між фактичними і розрахунковими значеннями функції -абсолютне і відносне; середнє відхилення між фактичними і розрахунковими значеннями функції - абсолютне і відносне (див. формули: 3.45; 3.46 ; 3,47 ; 3.48 ), які використовуються для оцінки рівняння часового тренда, у рівній мірі застосовуються і для оцінки статистичної адекватності економіко-статистичних моделей.
Для останніх додатково визначається залишкова дисперсія:

де m - число факторів, які включені у модель.
Залишкова дисперсія може бути використана і для оцінки рівняння часового тренда.
