4.2.6. Методи надання моделям статистичної надійності
Як відмічалося в минулому параграфі, головні проблеми, з якими стикається дослідник при побудові економіко-статистичної моделі - це мультиколеніарність; рівень істотності рівняння, параметрів і характеристик моделі, автокореляція.
Щоб забезпечити наукову і практичну цінність дослідження, необхідно:
• усунути мультиколеніарність;
• виключити неістотні за t-критерієм Стьюдента фактори;
• позбавитися автокореляції.
Найпростіший спосіб усунення мультиколеніарності полягає у виключенні з моделі одного з тісно пов'язаних між собою факторів. Виключений фактор вибирається або на основі логічного підходу, тобто на думку дослідника, або, використовуючи формальний підхід, вибирають той фактор, у якого тіснота зв'язку з результативним показником, що оцінена по значенню парного коефіцієнта кореляції, слабша. Але такий метод не завжди доцільний, тому, що покращуючи "статистичні якості" моделі, він одночасно нерідко знижує її аналітичну та прогнозну цінність. У економічному аналізі бажана певна комбінація факторів. Тому, щоб позбутися мультиколеніарності без виключення факторів з моделі, рекомендується здійснювати попереднє перетворення факторів, зокрема:
замість початкових даних, отриманих в результаті статистичного спостереження, слід скористатись їх першими різницями (yt-yt-1);
перетворити початкові дані, які мають тісний взаємозв'язок, у похідні величини, які являють собою співвідношення двох початкових. Перетворені величини при цьому мають виражати певну економічну суть.
При оцінці істотності параметрів та характеристик рівняння, а також і самого рівняння потрібно спочатку визначити, яка початкова інформація використовується для реалізації моделі. Якщо початкова інформація являє собою репрезентативну вибірку, то потрібен "жорсткий" підхід до оцінки істотності, тобто у всіх випадках має зберігатися умова (4.24). У протилежному
випадку, якщо розширення вибірки, доповнення складу факторів не сприяють виконанню вимоги (4.24), то таке рівняння виключається із дослідження.
Якщо ж рівняння істотне за F-критерієм Фішера, як і коефіцієнт множинної кореляції (множинне кореляційне відношення) за t-критерієм Стьюдента, але статистично неістотні за t-критерієм окремі коефіцієнти регресії, то, керуючись методикою багатокрокового регресивного аналізу, необхідно поступово виключати з рівняння статистично неістотні фактори. Формальне дотримання вказаної методики інколи призводить до того, що з рівняння виключаються найбільш суттєві фактори і цим самим знижується цінність моделі та її практичне використання. Такий підхід вважається негнучким і тому рекомендується виключати з рівняння фактор лише у тому випадку, коли квадратична помилка коефіцієнта регресії перевищує абсолютний розмір власне самого коефіцієнта, і при цьому, що найголовніше, коли немає сильних логічних підстав для виключення даної змінної. Таким чином віддається перевага якісному аналізу, тобто теоретичним основам процесу, перед кількісними, тобто формальними правилами математичної статистики.
Якщо ж, на відміну від репрезентативної вибірки, початкова інформація являє собою дані звітності по певному об'єкту за ряд років, то в такому випадку не доводиться говорити про випадкові змінні, і тому немає необхідності дотримуватись жорстких вимог та правил математичної статистики.
Існує декілька способів усунення автокореляції у динамічних рядах.
Перший метод - використання замість первинних початкових даних їх логарифмів, що означає перевагу логарифмічних моделей перед іншими при обробці динамічних рядів.
Другий метод - використання перших різниць.
Логарифмічне рівняння можна перетворити у лінійне; якщо позначити:
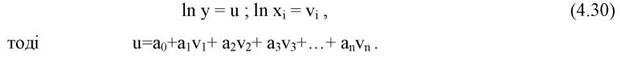
| Перші різниці дорівнюють |
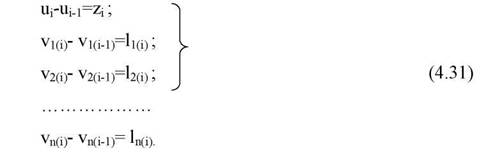
В цьому випадку система нормальних рівнянь реалізується для моделі
![]()
Для отримання прогнозу у прийнятих одиницях виміру виконуються наступні розрахунки:
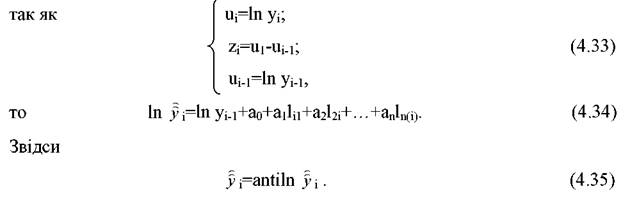
Третій метод - авторегресивне перетворення

де г - емпіричний коефіцієнт автокореляції. Прогнозні значення розраховуються наступним чином:
![]()
Виходячи з умовних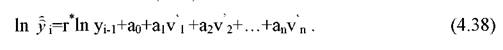 позначень і (4.37) Звідси
позначень і (4.37) Звідси
![]()
Четвертий метод - це включення фактору часу (t) у багатофакторні моделі. Вважається, що включення фактору (t) динамізує багатофакторну функцію при обробці динамічних рядів та виключає лінійну тенденцію у логарифмічних
даних (рівнозначно показниковій тенденції у початкових даних), що в результаті сприяє послабленню автокореляції.
Досвід показує, що логарифмування початкових даних (логарифмічна модель) в достатній мірі знижує автокореляцію.
Що ж до включення фактору часу t у багатофакторну модель, то крім послаблення автокореляції, деякі дослідники вважають, що у рівняннях виробництва продукції (виробнича функція) та продуктивності праці фактор часу служить вимірювачем технічного прогресу, хоча таке ствердження далеко не беззаперечне.
Проведені дослідження показали, що включення фактора часу t у деякі моделі інколи змінює економічно обгрунтовані взаємозв'язки між окремими факторами та досліджуваним показником. Тому вказаний фактор слід включити у багатофакторну модель лише у тому випадку, якщо він сприяє поліпшенню кількісних та якісних характеристик моделі, не порушуючи при цьому економічну суть рівняння.
Усі перелічені процедури підвищення статистичної надійності моделі слід здійснювати у взаємозв'язку з якісним (теоретичним ) аналізом результатів на всіх етапах проведення розрахунків.
