4.2.7. Економічний аналіз та прогнозування на основі застосування економіко-статистичних моделей

Основні статистичні характеристики моделі (4.42):

коефіцієнт множинної кореляції - R=0,914;

середня помилка апроксимації - £,=3,4%;

критерій Фішера (розрахунковий) - Fp=6,12 при FT=1,6;

критерій Стьюдента для R - tR=69,75 при tT=1,98(5% рівень істотності).

Наведене рівняння отримано шляхом виключення неістотних параметрів. При ti=1,98 істотність по розрахунковому значенню для коефіцієнтів регресії складає: ta =5,64; ta= 20,56; ta=3,46; ta=3,32.

Оскільки при побудові рівняння (4.42) використані не динамічні ряди, а просторові дані, перевірка на автокореляцію не проводиться.

Для превірки наявності (відсутності) мультиколеніарності розрахована система парних коефіцієнтів кореляції (табл. 4.1)

Таблиця 4.1

Парні коефіцієнти кореляції (г   )

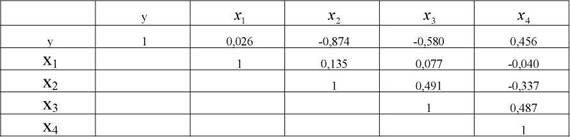
Мультиколеніарні зв'язки, як свідчать дані табл. 4.1, відсутні, оскільки коефіцієнти парної кореляції між факторами менше 0,8 за абсолютною величиною (див. рядки від 2-го до 5-го).

Таким чином, можна стверджувати, що модель (4.42) відповідає усім статистичним критеріям і тому статистично надійна.

*Примітка. Тут і надалі використані порівняні ціни, які діяли у дореформний період. Для ілюстрації методики та прикладів проведення розрахунків рівень прийнятих цін не має важливого значення.

Знаки перед коефіцієнтами регресії відповідають природі взаємозв'язків факторів із результативним показником; отже, модель відрізняється і логічною адекватністю.

Для проведення факторного порівняльного аналізу відібрані два підприємства із приблизно рівними початковими умовами: величиною добової потужності та тривалістю переробки цукрового буряка.

У табл. 4.2 наведений принцип проведення міжзаводського порівняльного аналізу із застосуванням залежності (4.40).

Таблиця 4.2

Порівняльний аналіз собівартості продукції

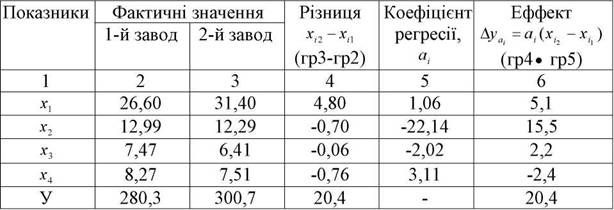
Дані табл. 4.2 свідчать про те , що виробнича собівартісь на другому заводі вища порівняно із першим на 20,4 крб. У гр.4 відображені результати порівняння факторів, які використовуються в моделі, та які визначають рівень виробничої собівартості продукції. Серед включених у модель факторів лише витрати палива на другому заводі нижчі ніж на першому. Щодо робочої сили, виходу цукру та фондовіддачі, то вказані показники на першому заводі кращі порівняно з другим заводом.

У гр. 6 подані характер та ступінь впливу факторів на рівень виробничої собівартості 1т. цукру-піску. В найбільшій мірі подорожчання собівартості на другому заводі пояснюється меншим, порівняно із першим заводом, виходом цукру у % до ваги переробленого буряка.

Порівняння витрат робочої сили на 100т буряка та фондовіддачі свідчить про те, що за рахунок названих факторів собівартість на другому заводі вища, порівняно із першим відповідно на 5,1 крб та 2,2 крб.

Моделі, які побудовані на основі просторових даних, в більшій мірі придатні для проведення аналізу та в меншій мірі - для складання прогнозу. Наведений вище приклад має аналітичну направленість та ілюструє можливість застосування рівнянь для проведення економічного аналізу.

Нижче розглядаються моделі, що побудовані на основі динамічних рядів, та які використовуються як в аналізі, так і в прогнозуванні.

У економічних дослідженнях широко використовуються рівняння, які відображають залежність обсягу випуску продукції від виробничих факторів (робочої сили, знарядь праці та засобів праці). Таке рівняння, відоме як виробнича функція Кобба-Дугласа, може бути побудована як на макро- так і на мікрорівні.

Виробнича функція Кобба-Дугласа зображається у вигляді двохфакторного степеневого рівняння

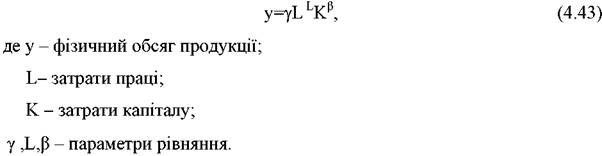
У практичних розрахунках на мікрорівні в якості фактору "затрати праці" використовується або чисельність працюючих, або кількість відпрацьованих людино-днів (людино-годин); а замість узагальнюючого показника "затрати капіталу" застосовуються показники вартості основних виробничих фондів та оборотних фондів.

Для зручності реалізації степенева функція перетворюється в логарифмічну і врешті модель приймає такий вигляд:

де у - фізичний обсяг продукції;

x1- чисельність працюючих або кількість відпрацьованих людино-днів (людино-годин);

x2 - вартість основних промислово-виробничих фондів; x3 - вартість оборотних фондів.

Рівняння (4.44), яке реалізоване на основі даних за ряд років по приладобудівному заводу, має такий вигляд:

ln y = 0,1484+0,4921 ln x1 + 0,0277 ln x2 + 0,6376 ln x3    (4.45) Статистичні характеристики рівняння (4.45) наведені у табл. 4.3

Таблиця 4.3 Статистичні характеристики рівняння (4.45)

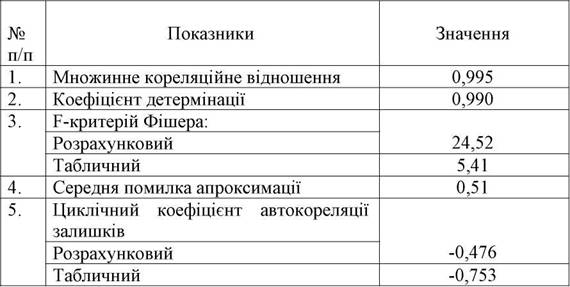
З даних табл. 4.3, випливає, що рівняння (4.45) відрізняється високими та надійними статистичними характеристиками. Розрахункове значення F -критерія Фішера більше табличного, що підтверджує істотність рівняння. Оскільки розрахункове значення циклічного коефіцієнта автокореляції залишків за абсолютною величиною менше табличного, то автокореляція залишків випадкова.

Велике значення множинного кореляційного відношення та незначне значення середньої помилки апроксимації показує, що побудоване рівняння адекватно відображає досліджуваний процес.

Нарешті, із значення коефіцієнта детермінації випливає, що включені у модель фактори на 99,0 % визначають рівень досліджуваного показника і лише 1 % - невраховані фактори .

Оскільки тобто сума коефіцієнтів

більша за одиницю, можна стверджувати про позитивний ефект розширення виробництва на підприємстві.

За значенням коефіцієнтів (аі), які в логарифмічному рівнянні являють собою коефіцієнти еластичності, можна оцінити вплив кожного фактору на досліджуваний показник.

Так, за досліджуваний період збільшення чисельності працюючих на 1% дозволило збільшити випуск товарної продукції в середньому приблизно 0,49%; збільшення вартості основних промислово-виробничих фондів на 1% забезпечило збільшення товарної продукції приблизно на 0,028%; нарешті збільшення вартості оборотних фондів на 1% забезпечило збільшення товарної продукції приблизно на 0,64% (всі цифри дещо округлені).

Розрахована за формулою (4.12) гранична віддача дозволяє зробити такі висновки: за досліджуваний період збільшення чисельності працюючих на підприємстві на 1 працівника забезпечило збільшення товарної продукції в середньому приблизно на 5,9 тис. крб.; із збільшенням вартості основних фондів на 1 тис.крб виробництво товарної продукції зросло в середньому приблизно на 0,03 тис. крб., збільшення обсягу оборотних фондів на 1 тис. крб відповідало збільшенню випуску товарної продукції в середньому приблизно на 1,39 тис. крб.

Функція випуску дозволяє відповісти на питання: - у якій мірі кожен із факторів сприяв росту результативного показника, у нашому випадку товарної продукції.

У лінійних рівняннях залежність

відображає приріст результативного показника за певний період під дією приросту виробничих факторів.

Для логарифмічних рівнянь випуску продукції залежність (4.46) приймає вигляд: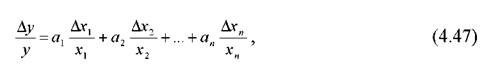

тобто темп приросту випуску продукції визначається зваженою сумою темпів приросту факторів , причому в якості вагів виступають відповідні коефіцієнти еластичності .

Розрахунки по оцінці впливу середнього приросту кожного фактору на загальний середньорічний приріст продукції , тобто реалізацію залежності (4.47), показано у табл. 4.4.

Таблиця 4.4. Оцінка впливу факторів на середньорічний приріст товарної

ПЮОЛУКШЇ

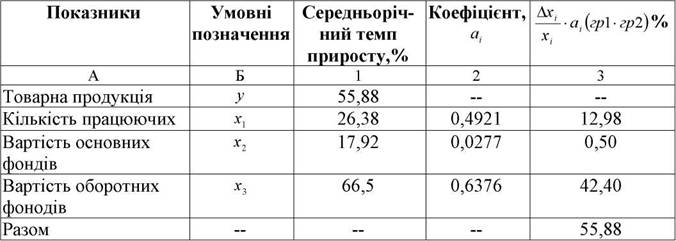
За данними табл. 4.4, середньорічний темп приросту товарної продукції за досліджуваний період становив 55,88%. У гр. 3 табл. 4.4 показано в якій мірі середньорічний темп приросту кожного фактора сприяв середньорічному темпу приросту товарної продукції. Підсумок гр.3 відповідає залежності (4.47) та дорівнює середньорічному темпу приросту товарної продукції по аналізованому підприємству.

За залежністю

визначити, у якій мірі кожний фактор сприяв середньорічному абсолютному приросту досліджуваного показника.

При середньорічному абсолютному прирості товарної продукції 7927 тис крб, приріст чисельності працюючих забезпечив середньорічний абсолютний приріст продукції на

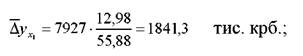
приріст вартості основних виробничих фондів забезпечив середньорічний абсолютний прирістпродукції на

та приріст вартості оборотних фондів забезпечив середньорічний абсолютний приріст продукції на

Сумарний вплив трьох факторів склав: 1841,3+70,9+6014,8=7927 тис. крб., що відповідає загальному середньорічному абсолютному приросту продукції.

Склад факторів, які включені у виробничу фукцію (4.44), хоча і застосовується для дослідження у багатьох галузях промисловості, не може бути канонізований через специфічні особливості різних виробництв. Так, для цукрової промисловості у зв'язку з сезонністю її виробничого процесу, переробки значної кількості сировини, що швидко псується (буряка), впливу на результати діяльності вмісту цукру у буряку, монопродуктовий характер виробництва, рівняння зі складом показників згідно моделі (4.44) не забезпечує досягнення поставленої мети по проведенню факторного аналізу випуску продукції, і тому такий склад невиправданий.

Досвід, накопичений в результаті багаторазових досліджень на різних рівнях управління, показав, що найбільш адекватно виробнича функція у цукровому виробництві описується рівнянням

де у - кількість виробленого цукру - піску;

x1 - кількість буряка, що залишився до переробки;

x2 - цукристість буряка, що залишився до переробки;

x3 - добова потужність.

Виробнича функція для цукрового виробництва відрізняється суттєвою перевагою порівняно із узагальнюючою функцію випуску (4.44): усі включені у модель показники подані натуральними величинами, тобто виключається вплив цінового фактору. Такі функції відображають ідеальний взаємозв'язок витрат та випуску продукції.

Реалізована на основі даних обласного об'єднання цукрової промисловості модель (4.49) має такий вигляд:

Показник (гранична віддача), розрахований згідно формули (4.12), дозволяє зробити такі висновки. За досліджуваний період при інших рівних умовах збільшення обсягу буряка на 1 тис. т дозволило збільшити виробництво цукру-піску приблизно на 0,11 тис.т; збільшення цукристості буряка на 1% дозволило збільшити виробництво цукру на 24,77 тис.т нарешті, збільшення добової потуж-ності на 1 тис.т дозволило збільшити виробництво цукру приблизно на 0,11 тис.т.

У цукровій промисловості збільшення потужності підприємств сприяє скороченню виробничого сезону; останнє ж дозволяє зменшити втрати буряка та цукру на усіх стадіях виробничого циклу.

Раніше відмічалося що взаємодіючі у рівнянні виробничої функції фактори по суті взаємозамінні. Це означає, що одиницю даного ресурсу можна замінити деякою кількістю іншого ресурсу так, що обсяг продукції при цьому не зміниться. Функція випуску для цукрової промисловості у найбільшій мірі відповідає умовам взаємозамінності ресурсів (факторів). Взаємозамінність для кожної пари факторів визначається за допомогою показника граничної норми зміщення, яка обчислюється як відношення величин граничної віддачі (залежність 4.13).

Економічна суть факторів, включених у функцію випуску для цукрової промисловості, дозволяє дати реальну інтерпретацію показника граничної норми заміщення. За досліджуваний період підвищення на 1% цукристості буряка рівнозначно з точки зору випуску продукції додатковій переробці

приблизно 225,2 тис. т буряка (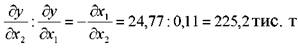) в умовах

базисної цукристості, тобто 1% приросту цукристості буряка дає таке ж збільшення виробництва цукру, що і 225,2 тис.т буряка при базисній цукристості. Збільшення добової потужності на 1 тис.т рівнозначно додатковій переробці приблизно 1 тис.т буряка.

Вище розглянуті аналітичні можливості економіко-статистичних моделей на прикладі виробництв, що відносяться до різних галузей промисловості.

Наступний етап застосування економіко-статистичних моделей - це прогнозування. Складність прогнозування на основі економіко-статистичних моделей полягає в тому, що перед тим як прогнозувати досліджуваний показник слід побудувати прогнози для всіх факторів, включених у рівняння. Вибір методів прогнозування факторних показників визначається як їх особливостями, так і особливостями виробництв.

Так, для функції випуску приладобудівного підприємства (модель 4.44) прогнозування очікуваних значень окремих факторів (xi) може бути проведено на основі застосування рівняння часового тренда.

У цукровій промисловості при побудові середньострокових прогнозів прогнозовані значення цукристості заготовленого буряка та очікуваного валового збору буряка визначаються на базі середнього рівня за попереднє п'ятиріччя. При оцінці валового збору спочатку визначається середня урожайність буряка з 1 га, яка потім перемножується на заплановану площу посіву. Добова потужність визначається планом вводу нових потужностей та реконструкції діючих.

Природно, названі методи рідко відрізняються достатньою точністю.

Короткострокове прогнозування у цукровій промисловості дозволяє досягти досить прийнятних результатів на основі моделі (4.49).

Для цього будується система прогнозних моделей, які дозволяють визначити очікуване значення факторів: x1 - обсяг заготовленого буряка та x2-цукристість заготовленого буряка (фактор x3 - добова потужність - відомий). Прогноз очікуваного обсягу виробництва цукру-піску складається на наступний виробничий рік.

Для оцінки очікуваного обсягу заготовленого буряка спочатку прогнозується середня урожайність на 1га, яка після множиться на площу посіву (величина відома).

Очікувана середня врожайність обчислюється за формулою

де   у - очікувана урожайність буряка у наступному році;

Р )1.10 - вага кореня за станом на 1 жовтня (методика розрахунку за формулою 3.22);

m 20.08 - густота насадження рослин на 1 га за станом на 20 серпня. Густота насадження рослин визначається двічі на рік: 1 липня і 20 серпня. Оскільки прогнозування урожайності починається з 1 липня, то до 20 серпня для рівняння (4.50) величина m 20,08 прогнозується за формулою

Починаючи з 20 серпня у формулі (4.50) використовуються фактичні дані. Цукристість заготовленого буряка прогнозується за формулою:

де D3 - прогноз цукристості заготовленого буряка;

Di ю - прогноз цукристості корнеплодів на 1 жовтня, який розраховується, починаючи з 20 липня за тією методикою, що і вага корнеплода (залежність 3.29)

У табл. 4.5 наведені дані про фактичні та прогнозовані значення середньої урожайності та цукристості буряка.

Таблиця 4.5

Порівняння фактичних та прогнозованих значень середньої урожайності та цукристості заготовленого буряка

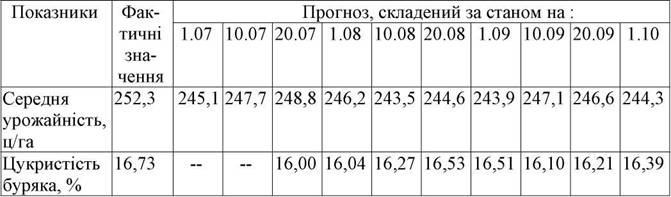
Таким чином, як свідчать дані табл. 4.5, розходження між фактичною урожайністю та прогнозованими значеннями незначні та коливаються в межах від 1.4% до 3.5%. Абсолютні відхилення по цукристості буряка складають від 0,20% до 0,73%, причому по мірі наближення до початку виробничого сезону точність прогнозу збільшилась.

За значенням прогнозованої середньої урожайності та площах посівів розраховані очікувані валові закупки буряка. У прогнозованому періоді розходження між фактичним обсягом заготовленого буряка та прогнозом склало 0,1^-2,0%, у той час, як порівняно із планом об'єднання фактичні значення були менші на 19,6%.

Визначивши прогнозовані значення валових заготовлень і цукристості буряка та використовуючи дані про величину виробничої потужності, можна застосувати модель (4,50) для прогнозування очікуваного обсягу виробництва цукру-піску із буряка. Розходження між фактичним та прогнозованими значеннями обсягу виробництва цукру досягає максимум 10-12%, що з урахуванням впливу багатьох факторів на виробничий процес, та в першу чергу якості буряка, погодних умов, у певній мірі припустимі. Розходження між фактичними значеннями та планом об'єднання більш значні.

Спектр методів прогнозування урожайності та цукристості буряка можна розширити. Нарівні із використанням середніх приростів для прогнозування урожайності та цукристості буряка на 1 жовтня (залежність 3.29) можна скористатися рівнянням

тобто обчислити значення показника за станом на певну декаду в залежності від значення цього ж показника за попередню декаду.

В процесі проведення економічних досліджень, в т.ч. і в прогнозуванні дуже важливо багаторазове використання наявної інформації для обчислення як можна більшого числа показників, необхідних для управління виробництвом. Наявність прогнозованого значення валових заготовлень буряка та величини добової потужності дозволяє скласти прогноз тривалості сезону переробки буряка, який має суттєвий вплив на кінцеві показники діяльності цукрових заводів

де у - прогноз тривалості виробництва, діб;

х і -прогнозоване значення обсягу заготовлення буряка;

x2 - добова потужність

За рівнянням ізокванти

можна визначити необхідний обсяг буряка для кожного заводу, об'єднання при фіксованому значенні тривалості виробництва.

Розрахунки за залежністю (4.56) важливі для перерозподілення буряка між заводами для рівномірної їх загрузки, що значно скорочує втрати цукру

Аналогічно рівнянням тимчасового тренду економічко-статистичні моделі можуть бути використані для прогнозування не лише безпосередньо, а і опосередковано через систему залежностей, виведених на основі параметрів рівняння. Висловлену вище думку розглянемо на прикладі моделювання залежності повної собівартості продукції і окремих статей витрат від обсягу продукції при фіксованих цінах. Для цього використана модель

де уі - витрати по відповідних статтях витрат та в цілому по повній собівартості продукції у порівняних цінах;

х - обсяг товарної продукції у порівняних цінах.

Показники ан , які розраховані по всій номенклатурі статей витрат, являють собою коефіцієнти еластичності, тобто відображають темп приросту кожної статті витрат під впливом швидкості зміни обсягу товарної продукції. Звідси аі=Еі.

Якщо усі показники приведені до єдиних цін та умов, то прогнозовані значення повної собівартості товарної продукції чи окремих статей витрат може бути визначено за формулою

а відносна економія за рахунок умовно - постійних затрат, яка є у меншій чи більшій мірі практично у всіх статтях витрат, дорівнює

де y))і(t+1)- очікуване значення прогнозованого показника (стаття витрат, повна собівартість);

Еі - коефіцієнт еластичності для і-го показника;

Тпр(х) - темп приросту обсягу товарної продукції у прогнозованому періоді порівняно з базисним періодом;

yі(t) - значення і-го показника в базисному періоді .

Оцінка взаємозв'язку обсягу виробництва та витрат на виробництво має важливе значення при порівнянні різноманітних варіантів розвитку та розміщення підприємств, у процесі вибору оптимального розміру підприємства (обсягу випуску продукції) та прогнозуванні затрат на виробництво.

Коефіцієнти еластичності, які відображають відносний взаємозв'язок обсягу виробництва та затрат на виробництво, можуть бути одночасно використані для оцінки частки постійних витрат

де уіпр - питома вага постійних витрат в і-тій статті витрат чи в повній собівартості.

Дійсно, якщо, наприклад, для певної статті витрат Е=0,402, то можна зробити висновок, що в середньому за досліджуваний період змінні витрати в даній статті складають 40,2%, а постійні упрв = 100(1-0,402)=59,8%.

В цілому прогноз на підставі економіко-статистичної моделі складається на підставі рівнянь:

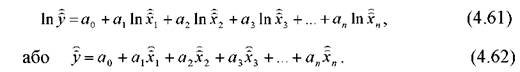
Вище, на декількох прикладах, наведений підхід щодо прогнозування деяких показників на основі економіко-статистичних моделей.

Дати рекомендації на всі можливі випадки неможливо, оскільки, не дивлячись на практичне застосування обмеженого кола видів багатофакторних моделей, склад показників, які входять у рівняння, дуже різноманітний. Вибір методики прогнозування окремих показників визначає дослідник, керуючись особливістю виробництва, змістом досліджуваних показників, наявною інформацією технічними і програмно-методичними можливостями.

Оцінка точності прогнозу на основі економіко-статистичних моделей здійснюється тими ж показниками, які застосовуються при оцінці точності прогнозу на основі рівняння часового тренда (залежності 3.54; 3.55; 3.56; 3.57; 3.58; 3.59; 3.60; 3.61)

Інтервал довіри для прогнозів, побудованих на основі економіко-статистичних моделей, дорівнює

де tт - табличне значення t-критерія Стьюдента при заданому рівні істотності та кількості елементів у вибірковій сукупності;

де уt - фактичне значення досліджуваного показника;

у t — розрахункове,  на основі рівняння,  значення досліджуваного показника;

п - кількість елементів у вибірковій сукупності; m - кількість факторів, які включені у модель.