4.4. Логічні основи теоретичного рівня пізнання
4.4. Логічні основи теоретичного рівня пізнання
На теоретичному рівні пізнання використовуються різні форми умовиводів. Умовивід — це форма мислення, в якій з одного чи декількох істинних суджень на основі певних правил виводу виводять нове судження. Структура кожного умовиводу включає засновки, висновок і логічний зв’язок між засновками та висновком. Умовивід буде правильним тоді і тільки тоді, коли в ньому виконуються основні закони логіки (тотожності, несуперечності, виключеного третього, закон достатньої підстави). Логічним висновком з даних засновків є таке речення, яке не може бути хибним, коли ці засновки істинні. Умовиводи поділяються на дедуктивні, індуктивні та традуктивні (умовиводи за аналогією). Вони можуть бути необхідними та ймовірними (правдоподібними).
Дедуктивний умовивід — це умовивід, в якому висновок обов’язково зроблений із засновків, які виражають знання достатньо великого ступеня загальності і які самі є знанням меншого ступеня загальності.
Логічне слідування іде від роду до виду, від загального класу до підкласу. Правила виводу повинні задовольняти ряд вимог: по-перше, з істинних засновків вони повинні дозволяти виводити тільки істинні судження; по-друге, правила виводу повинні бути несуперечними (сумісними) в даній логічній системі, тобто неможливо одним способом з одних і тих самих засновків виводити висновок «а», а другим способом — «не-а»; по-третє, необхідно виходити з наявності повноти системи, а це означає: користуючись тільки даними правилами виводу в даній логічній системі, можливо вивести будь-які змістовоістинні висновки, що сформульовані в термінах даної системи й логічно випливають з даних засновків.
Правила прямого виводу дають можливість з наявних істинних засновків одержати істинний висновок. Правила непрямого виводу дають змогу робити висновок про правомірність деяких висновків із правомірності інших.
Безпосередніми умовиводами називаються дедуктивні умовиводи, які виводять з одного засновку. До них належать перетворення, обернення, протиставлення предикатові та умовивід за логічним квадратом.
Перетворення — вид безпосереднього умовиводу, в якому змінюється якість засновків без зміни їхньої кількості, тобто змінюються на протилежні якість зв’язку і якість предиката. Перетворенню підлягають усі чотири види суджень (А, Е, І, О).
Оберненням називається такий безпосередній умовивід, в якому у висновку (новому судженні) суб’єктом стає предикат, а предикатом — суб’єкт. Обернення бувають прості (без обмежень) і з обмеженнями. Частково заперечні судження не обертаються. Прості обернення утворюються тоді, коли як S, так і Р вихідного судження або розподілені, або нерозподілені. Обернення з обмеженням можна зробити тоді, коли у вихідному суджені суб’єкт є розподіленим, а предикат — нерозподіленим, або, навпаки, суб’єкт є нерозподіленим, а предикат — розподіленим.
Протиставлення предикатові — такий безпосередній умовивід, у якому в новому судженні (тобто висновку) суб’єктом виступає поняття, що суперечить предикату вихідного судження,
а предикатом є суб’єкт вихідного судження, причому зв’язка змінюється на протилежну. Алгоритмом для отримання висновку є такі кроки: по-перше, перетворити засновок, по-друге, перетворене судження обернути. Для судження (І) операція протиставлення предикатові не є коректною.
Протиставлення суб’єктові — такий безпосередній умовивід, у якому предикат вихідного судження стає суб’єктом висновку,
а предикатом висновку береться поняття, суперечне суб’єктові засновку. При цьому якість судження завжди змінюється. Алгоритмом для отримання висновку є такі кроки: спочатку вихідне судження обертається, а потім результат перетворюється.
Для судження (О) операція протиставлення суб’єктові не є коректною.
Безпосередній умовивід за логічним квадратом за суттю є трансформацією заданого судження (засновку) у три інших судження, з яких лише одне може бути істинним. Разом із засновком висновки складають 4 судження, причому 2 з них є істинними і 2 — хибними.
Категоричний силогізм — це вид дедуктивного умовиводу,
в якому з двох категоричних суджень, пов’язаних середнім терміном (М), при додержанні правил обов’язково повинні бути два засновки і висновок. Поняття, що входять до складу силогізму, називаються його термінами.
Більший засновок має в собі більший за обсягом термін, менший засновок має менший термін. В основі висновку в категоричному силогізмі лежить аксіома силогізму: «Все, що стверджується або заперечується стосовно виду (або члена даного класу), належить до даного роду».
Фігурами силогізму називаються форми силогізму, які розрізняються за положенням середнього терміна М у засновках і обов’язково наявністю предиката у більшому засновку і суб’єкта у меншому засновку (схема 3).
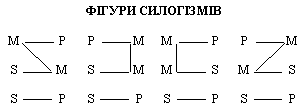
Модусами категоричного силогізму називаються його різновиди, що відрізняються один від одного якісною та кількісною характеристиками засновків, що входять до нього, є висновком. Кожна фігура силогізму має певну кількість правильних модусів, тобто формул коректних рішень:
перша фігура — ААА, ЕАЕ, АІІ, ЕІО;
друга фігура — ЕАЕ, АОО, АЕЕ, ЕІО;
третя фігура — ОАО, ААІ, АІІ, ІАІ, ЕАО, ЕІО;
четверта фігура — ААІ, ЕАО, ІАІ, ЕОІ, АЕЕ.
Правила для термінів категоричного силогізму:
В кожному силогізмі повинно бути тільки 3 терміни (S, Р, М);
Середній термін (М) повинен бути розподілений хоча б в одному із засновків;
Термін, не розподілений у засновку, не може бути розподіленим у висновку.
Правила для засновків категоричного силогізму:
З двох заперечних засновків не можна зробити ніякого висновку;
Якщо один із засновків заперечний, то й висновок повинен бути заперечним;
З двох часткових засновків висновку робити не можна;
Якщо один із засновків частковий, то й висновок повинен бути частковим.
Таблиця 18
ТАБЛИЦЯ ВИДІВ УМОВНИХ І РОЗДІЛОВИХ УМОВИВОДІВ
| Назва умовиводів | Формули |
| 1. Суто умовний умовивід (обидва засновки і висновок є умовними судженнями) |
|
| 2. Умовно-категоричні умовиводи (другий засновок і висновок — категоричні судження) |
|
| 2.1. Стверджувальний модус (менший засновок стверджує підставу, а висновок — наслідок умовного судження) |
|
| 2.2. Заперечний модус (менший засновок заперечує наслідок, а висновок — наслідок) |
|
| 3. Розділово-категоричні умовиводи (другий засновок — категоричне, а висновок — категоричне або розділове судження) |
|
| 3.1. Завжди розділовий засновок (правильні розділово-категоричні умовиводи) |
|
| 3.2. Стверджувально- |
|
| Назва умовиводів | Формули |
| 4. Умовно-розділові умовиводи |
|
| 4.1. Проста конструктивна дилема |
|
| 4.2. Складна конструктивна дилема |
|
| 4.3. Проста деструктивна дилема |
|
| 4.4. Складна деструктивна дилема |
|
Умовні умовиводи завжди включають до свого складу як перший засновок умовне судження. Залежно від того, якими судженнями (умовними, категоричними чи розділовими) є другий засновок і висновок, умовні судження поділяються на суто умовні, умовно-категоричні та умовно-розділові. У суто умовному умовиводі обидва засновки і висновок є умовними судженнями;
в умовно-категоричному умовиводі другий засновок і висновок є категоричними судженнями.
Розділові умовиводи завжди включають до свого складу
як перший засновок розділове судження. До складу суто розділового умовиводу входять тільки розділові судження; у розділово-категоричному умовиводі перший засновок розділовий, другий засновок є категоричним, а висновок — категоричним або розділовим; у розділово-умовному умовиводі перший засновок є розділовим, а інші — умовними судженнями (табл. 18).
Індуктивні умовиводи — це опосередковані умовиводи, в котрих з одиничних суджень-засновків виводять часткове або й загальне судження-висновок. У гносеології індукцією називають метод наукового пізнання, який полягає в дослідженні процесу пізнання від одиничного до часткового або загального. Існують повна і неповна індукції. Неповна індукція в свою чергу поділяється на наукову і популярну.
Повна індукція — це різновид індуктивного умовиводу, в якому на підставі значення про належність певної ознаки кожному предметові класу робиться висновок про належність цієї ознаки всім предметам цього класу. Схема повної індукції має вигляд:
1) S1 є Р
S2 є P
S3 є Р
…
Sn є Р
2) Відомо, що S1, S2, S3 ….. Sn вичерпують клас S
Отже, S є P.
Умовивід за повною індукцією є необхідним, тобто його вірогідність дорівнює одиниці (Р = 1).
Неповна індукція — це індуктивний умовивід, в якому висновок про весь клас предметів робиться на підставі знання тільки деяких предметів цього класу. Її схема:
1) S1 є Р
S2 є P
S3 є Р
…
Sn є Р
2) S1, S2, S3 ….. Sn належать до класу К
Отже, можливо, клас К має Р.
Умовивід за неповною індукцією є ймовірним, тобто його вірогідність менше одиниці і більше нуля (0 < P < 1).
Аналогія — це традуктивний умовивід (від лат. traductio — переміщування, перенесення), в якому на підставі подібності предметів в одних ознаках робиться висновок про їхню подібність в інших ознаках. Її схема має вигляд:
А має ознаки a b c d
В має ознаки a b с
Ймовірно, що В має ознаку d.
Існує проста аналогія, в якій на підставі подібності предметів за одними якими-небудь ознаками роблять висновок про їхню подібність в інших ознаках. Є також строга аналогія, що ґрунтується на знанні залежності ознак предметів, які порівнюються, й нестрога аналогія, в якій робиться висновок без знання про зв’язок подібних ознак. Усі тести на IQ перевіряють здібності людей розв’язувати задачі за аналогією.
