5.5. Визначення кiлькiсних параметрiв та показникiв експертного опитування
Питання, якi є в опитувальних анкетах, можуть бути орiєнтованi на оцiнку часу та ймовiрностi настання рiзних подiй, визначення кiлькiсних значень параметрiв та показникiв, оцiнку питомої ваги рiзних варiантiв рiшень, оцiнку вiдносної важливості параметрiв, факторiв, напрямкiв розвитку.
При оцiнці часу здійснення певної подiї або визначення кiлькiсних значень показникiв та параметрiв в якостi узагальнюючих характеристик даних експертного опитування вживаються мода, медiана, верхній та нижній квартілi.
Визначення узагальнюючих характеристик розглянемо на наступному прикладi.
Групi експертiв було задане запитання про час здiйснення певної подiї. Пiсля проведення четвертого туру отриманi наступнi результати (табл.5.1)
| Таблиця 5.1 |
| Інтервальний ряд розподiлу часу здiйснення подiї |
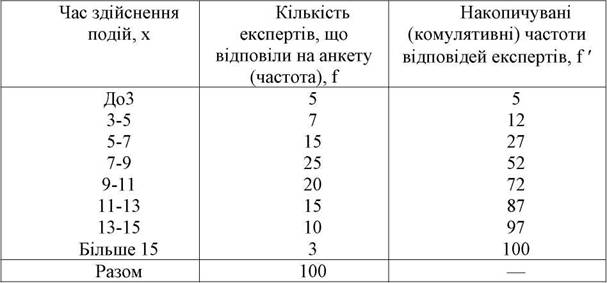
Комулятивна частота визначається послiдовним накопичуванням первинних частот. Для визначення комулятивних частот можна скористатися такими залежностями:
Мода та медiана — це рiзновиди середнiх величин, які називаються умовно структурними середніми.
Мода — це величина ознаки, яка найчастiше зустрiчається у вибiрковiй сукупності. Медiана умовно дiлить ряд розподiлу на двi рiвнi частини.
Мода в iнтервальному варiацiйному ряді обчислюється за формулою
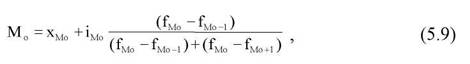
де Xmo— мiнімальне значення ознаки модального iнтервалу (модальним
вважається iнтервал з найбiльшою частотою); іmo— розмiр модального iнтервалу;
fmo>fmo-i>fmo+i - вiдповiдно значення частот модального iнтервалу, iнтервалiв, якi передують i слiдують за модальним.
В нашому прикладi модельний iнтервал — це 7-9, тому що для нього характерна найбiльша частота ( f=25).
Звiдси, з врахуванням даних табл. 5.1.
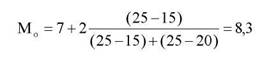
Отже, найбiльше число експертiв передбачає настання подiї орiєнтовно через 8 рокiв. Медiана в iнтервальному варiацiйному рядi обчислюється за формулою
Вiдповiдно з даними табл. 5.1. медiанний iнтервал складає 7-9, тобто спiвпадає з модальним iнтервалом.
Якщо підставити вiдповiднi данi в формулу (5.10), отримаємо
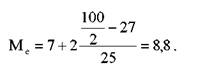
Аналiз величини медiани дозволяє зробити висновок про те, що перiод 8,8 рокiв дiлить усiх експертiв на двi рiвнi частини: перша частина експертiв передбачає здiйснену подiю до названої величини; друга, яка рiвна за величиною першiй, обумовлює здійснення подiї пiсля 8,8 рокiв з початку відліку (базисного перiоду).
Такого роду розрахунки, які доповненi квартілями, здiйснюються пiсля кожного туру опитування, результати повiдомляються кожному експерту.
Для оцiнки питомої ваги рiзних видiв рiшень для зручностi будується гiстограма. Шкала гiстограми дiлиться на декiлька частин, наприклад, на п'ять частин. Кожна така частина вiдображає ширину iнтервалу в 20 вiдсоткiв.
Висота стовбця в гiстограмi пропорцiйна питомiй вазi (в %) числу оцiнок в серединi певного iнтервалу.
В економiчному прогнозуваннi широке розповсюдження отримала оцiнка порiвняльної важливостi окремих факторiв (параметрiв, напрямкiв). Оцiнка експертом вiдносної важливостi факторiв здiйснюється, як правило, шляхом присвоєння деякої кiлькісної оцiнки, наприклад, за 100-бальною системою. Експерт надає кожному фактору (параметру, напрямку) кiлькiсть балiв в межах вiд 0 до 100. Нуль присвоюється в тому випадку, якщо фактор, на думку експерта, не має суттєвого значення, 100 балiв присвоюється тому фактору, який має найбiльш важливе вирішальне значення. Експерт може надати однакову кiлькiсть балiв декiльком факторам, якщо на його думку вони в рiвному ступенi суттєві. При обробцi матерiалiв колективної експертної оцiнки вiдносної ваги факторiв (параметрiв, напрямку) доцiльно використовувати метод рангової кореляцiї. Тому данi, отриманi в балах, вiдповiдним чином ранжують по мiрi зменшення та отримують оцiнки рангiв. Порядковий номер, що визначає мiсце кожного фактора в загальнiй сукупності факторiв, називається рангом. Зазвичай ранги вiдповiдають числам натурального ряду 1, 2, 3,... n, де n — кiлькiсть ранжованих факторiв. Ранг, рiвний одиницi, присвоюється найбiльш важливому фактору; ранг з максимальним числом n — найменш важливому фактору. Якщо експерт присвоює однакову кiлькiсть балiв декільком факторам, то їм присвоюється стандартизованi ранги. Стандартизований ранг — це частка вiд дiлення суми мiсць, зайнятих факторами з однаковими рангами, на загальну кiлькiсть таких альтернатив.
Наприклад. Припустимо, що експерт поставив напрямкам дослiджень такі бали: 100, 90, 90, 90, 80, 60, 50, 50, 40.
Тодi займанi мiсця кожного напрямку згiдно з кiлькiстю балiв складають: 1; 2-4; 5; 6; 7-8; 9.
Використовуючи правила визначення стандартизованих рангiв, отримаємо такі їх значення: 1; 3; 3; 3; 5; 6; 7,5; 7,5; 9, де 3=(2+3+4):3; 7,5=(7+8):2. Введемо такі умовнi позначення вихiдних даних:
m — кiлькiсть експертiв, що взяли учaсть в колективнiй експертнiй оцiнцi; 1, 2, 3,..., i,...,m — можливi номери експертiв; п — кiлькiсть напрямкiв дослiджень, що запропонованi до оцiнки; 1, 2, 3,...,j,...,n — можливi номери напрямкiв дослiджень; mj — кiлькiсть експертiв, які оцінили j-ий напрямок;
m100j-кiлькiсть максимально можливих оцiнок (100 бaлiв), отриманих j-им напрямком дослiджень;
Cij— оцiнка вiдносної ваги (в балах), даних і-ому експертом j-ому
напрямку дослiджень.
Всi бальнi оцiнки експертiв, що приймають значення вiд 0 до 100, можна розмiстити в окрему матрицю (таблицю). (таблиця 5.2).
Таблиця 5.2
МАТРИЦЯ БАЛІВ
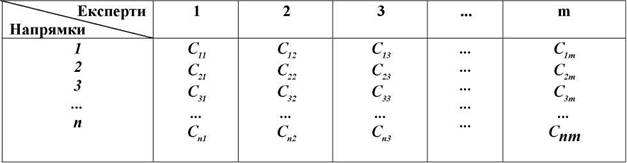
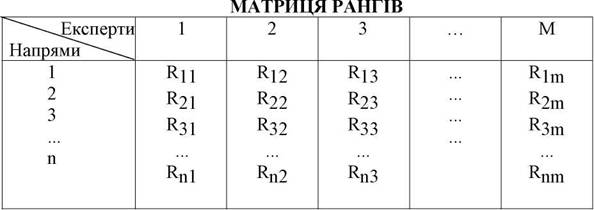
Таблицю балiв необхiдно перетворити в таблицю (матрицю) рангiв методом, викладеним вище, тобто елементи матрицi балiв Сij перетворюються
в елементи матрицi рангiв Rij. Rij — це ранг оцiнки i-м експертом j-го напрямку
(таблиця 5.3).
При обробцi результатiв експертних оцiнок по вiдноснiй важливості напрямкiв визначається ряд статистичних характеристик, на основi яких оцiнюється кожний напрямок (параметр, фактор).
Tаблиця 5.3
Процедура обробки даних анкет опитування розглядається на умовному прикладі.
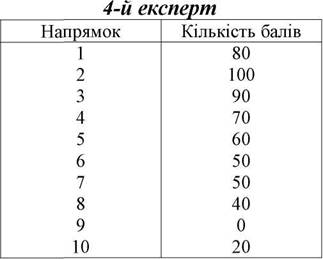
Є такі данi про результати оцiнки десяти напрямкiв, поданих чотирма експертами.
1-й експерт
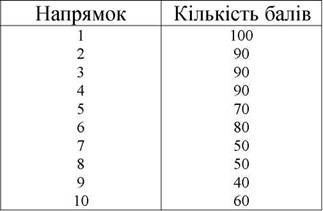
2-й експерт
| Напрямок | Kількість балів |
| 1 | 100 |
| 2 | 100 |
|
| 80 |
| 4 | 70 |
| 5 | 90 |
| 6 | 60 |
| 7 | 60 |
| 8 | 60 |
| 9 | 50 |
| 10 | 50 |
3-й експерт
|
|
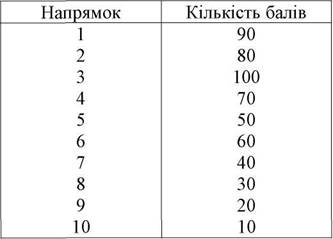
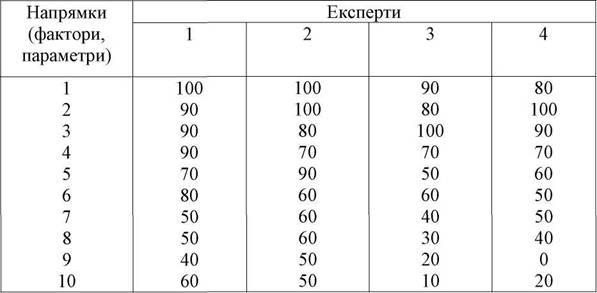
На основi даних опитування сформована матриця балiв (табл. 5.4)
Tаблиця 5.4
МАТРИЦЯ БАЛІВ ОЦІНКИ НАПРЯМКУ РОЗВИТКУ
|
|
Матрицю балiв перетворюємо в матрицю рангiв (табл. 5.5).
Таблиця 5.5
МАТРИЦЯ РАНГІВ ОЦІНКИ НАПРЯМКУ РОЗВИТКУ
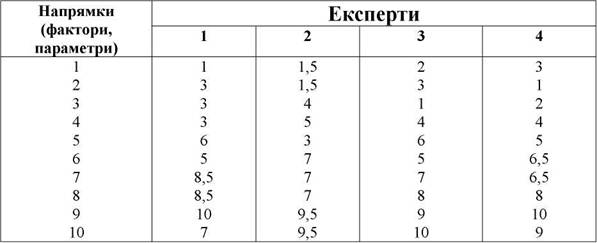
Сума рангiв, призначених експертами j-ому напрямку дослiджень, визначається за формулою
|
|
Для першого напрямку сума рангів дорiвнює S1=1+1,5+2+3=7,5
Для другого напрямку сума рангiв дорiвнює S2=3+1,5+3+1=8,5
Аналогiчно визначається для усiх напрямкiв. Очевидно, чим менша сума рангiв, тим важливіший певний напрямок.
Середнiй ранг для кожного напрямку дорiвнює
|
|
Для першого напрямку середнiй ранг дорiвнює
|
|
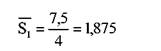
Для другого напрямку середнiй ранг дорiвнює
При порiвняннi важливостi рiзних напрямкiв по Sj найбiльш важливим слiд вважати напрямок, що характеризується найменшим значенням середньої величини рангу.
Поряд з середнiми рангами для кожного напрямку визначається середня величина в балах
Середнє значення (Mj) може приймати значення вiд 0 до 100 в залежностi вiд того, яку оцiнку вiдповiдно з важливістю дали експерти тому чи iншому напрямку.
Середнє значення (в балах) для першого напрямку дорiвнює
M1= (100+100+90+80):4=92,5 бала.
Аналогiчно визначаються середнi значення i для iнших напрямкiв.
Нагадаємо, що при визначенні середнього значення в балах, враховується тільки та кількість експертів, котра дала оцінку певному напрямку. Оскільки дев'ятому напрямку один з експертів не поставив кількість балів, то в такому випадку середня кількість визначається без урахування одного експерта, тобто
М9= (40+50+20)/3=36,67 бала.
Чим більше значення Мj, тим більше, на думку експертів, важливість розвитку j-го напрямку.
При оцінці важливості окремих напрямків представляє інтерес показник частоти максимально можливих оцінок, що визначається за формулою
Показник КШ]. може приймати значення в межах від 0 до 1. Важливість j-го напрямку збільшується при зміні K100j від 0 до 1.
Для першого і для другого напрямків K100j дорівнює
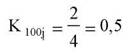
Для третього напрямку КЮОі буде дорівнювати
Для всіх інших семи напрямків K100j= 0.
Показник K100j слід розглядати як додатковий до інших показників оцінки
відносної важливості напрямку. Він характеризує важливість розвитку j-го напрямку з точки зору кількості поставлених йому перших місць. Перевагу тому чи іншому напрямку слід віддавати в першу чергу в залежності від середніх величин рангу чи балів. І тільки при інших рівних умовах напрямок можна вважати найбільш важливим при максимальному значенні КШ]..
Крім абсолютних величин оцінки важливості напрямку при обробці даних анкет опитування застосовуються також відносні показники. Для цього індивідуальні показники спочатку нормуються, а потім обчислюються середньозважені величини. Нормування - це перехід від абсолютних величин до відносних.
Середня вага кожного напрямку (нормована оцінка) розраховується за формулою
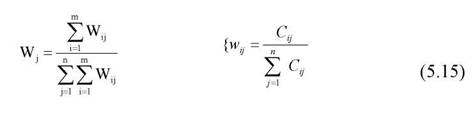
За даними табл. 5.4:
Wi i=100:(100+90+90+90+70+80+50+50+40+60)=0,139;
W2.1=90:(100+90+90+90+70+80+50+50+40+60)=0,125; W3.1=90:(100+90+90+90+70+80+50+50+40+40)=0,125. Аналогічно визначаються W і для кожного напрямку та по кожному експерту.
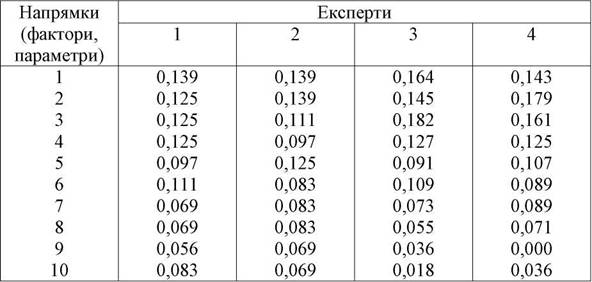
В табл. 5.6 наведені дані відносних показників по кожному напрямку з урахуванням думки окремих експертів.
Таблиця 5.6
МАТРИЦЯ ВІДНОСНОГО ЗНАЧЕННЯ НАПРЯМКІВ (ФАКТОРІВ,ПАРАМЕТРІВ)
Оскільки сума відносних значень, поставлених кожним експертом всім напрямкам, дорівнює 1, то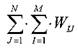
по суті дорівнює кількості експертів, що
беруть участь в експертизі. Тому
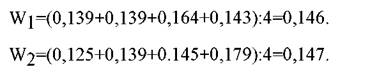
Аналогічно обчислюються середні відносні значення по всіх напрямках.
На основі матриці рангів будуються матриця переваги, суть якої полягає в тому, щоб оцінити, скільки експертів віддають перевагу даному напрямку порівняно з іншими, або, іншими словами, матриця переваг визначає число випадків, коли напрямокj , визначається як більш важливий за напрямок Z.
Матриця переваг, показники якої обчислені на основі даних матриці рангів (табл. 5.5), наведена в таблиці 5.7.
МАТРИЦЯ ПЕРЕВАГ
Таблиця 5.7
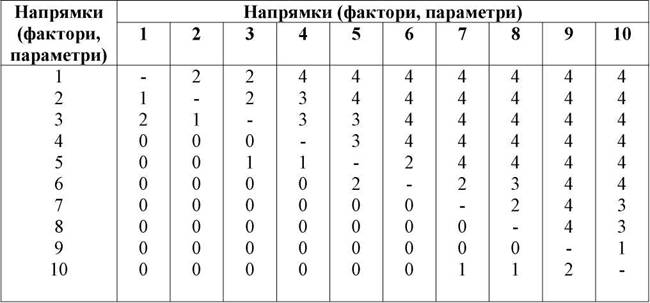
Матриця переваг будується таким чином. Для визначення елемента 1.2 (клітка на перетині 1-го рядка та 2-го стовпця) матриці переваги аналізуються рядки 1 та 2 матриці рангів табл.(5.5) і визначається, скільки разів ранги першого напрямку вище в порівнянні з рангами другого напрямку, або, іншими словами, скільки разів елементи першого рядка менше елементів другого рядка;
для розрахунку елемента 1.3 порівнюються рядки 1 та 3 матриці рангів, а потім виконуються ті ж дії, що і раніше, і т. д.;
для розрахунків елементів матриці переваг 2.1, 2.3, 2.4 порівнюються елементи матриці рангів 2-го рядка послідовно з 1-им, 3-им, 4-им рядками. Подальші дії аналогічні розрахункам першого рядка матриці переваг.
Таким методом обчислюються всі рядки матриці переваг.
Оскільки оцінки, поставлені кожним експертом окремим напрямкам різняться, як правило, значно, доцільно обчислювати розмах, використовуючи для цього залежність
де L- розмах оцінок, в балах, даних j-му напрямку,
Cjmax, Cjmin- відповідно максимальні та мінімальна оцінки, поставлені j-му напрямку окремим експертом.
Активність експертів по кожному напрямку обчислюється за допомогою коефіцієнта активності
де Каэj- коефіцієнт активності експертів по j-му напрямку; m- кількість експертів, що оцінили j-й напрямок; m - загальна кількість експертів.
В табл. 5.1 наведені показники, що відображають порівняльну важливість напрямків, обчислених за формулами (5.11-5.17)
Таблиця 5.8
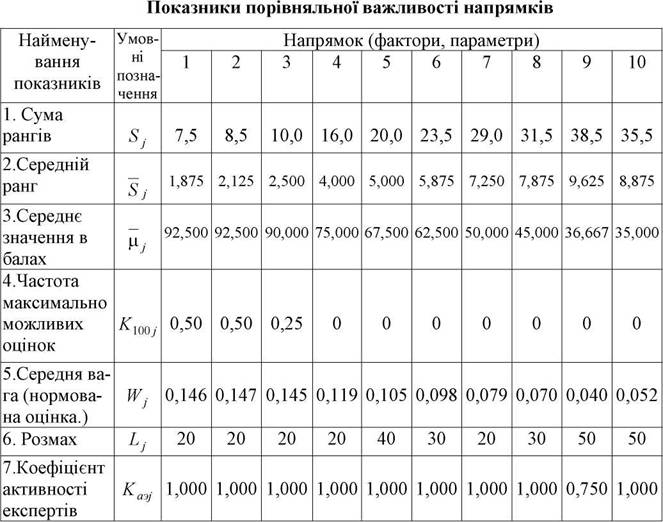
Оцінка показників відносної важливості напрямків, що містяться в табл. 5.1, свідчать про те, що група експертів віддала перевагу в основному першому
та другому напрямкам і менш схильна вважати доцільним 10-й і особливо 9-й напрямок. Разом з тим, як показує величина розмаху, за виключенням 5-го, 9-го та 10-го напрямків особливого розмаху в оцінках експертів не спостерігається.За значенням показника активності експертів можна судити, з одного боку, про компетентність експертів, а з іншого боку, що всі напрямки досить обгрунтовані, оскілки, за виключенням 9-го напрямку, всі експерти дали оцінку запропонованим напрямкам. Показники частоти максимально можливих оцінок свідчать про те, що тільки для трьох напрямків експерти призначили 100-бальну оцінку, з них для перших двох напрямків двічі, для третього - один раз.
Таким чином, організатори експертизи повинні з перших двох, а можливо навіть з перших трьох напрямків шляхом співставлення та додаткових оцінок вибрати найбільш прийнятний напрямок.