6.2. Методи аналізу і прогнозування ризику

У сучасній економічній практиці аналіз ризику поділя­ють на два види:

· якісний, головне завдання якого визначити чинники ризику, етапи і роботи, під час виконання яких ризик виникає, тобто встановити потенційні зони ризику, після чого ідентифікувати усі можливі ризики;

· кількісний, який застосовується для визначення чисельних окремих ризиків і ризику проекту в цілому. При кількісному аналізі ризику можуть використовуватися різноманітні методи.

Найбільш поширеними є: аналіз за допомогою бета-коефіцієнта, метод визначення імовірності результатів, аналіз сценаріїв, метод моделювання, аналіз чутливості реагуван­ня, теорія ігор.

Аналіз ризику за допомогою бета-коефіцієнта

В якості міри ризику в інвестиційній теорії використовується бета-коефіцієнт. Він виражає «ринкову чутливість» інвестиції, або на скільки змінюються доходи від капіталов­кладень у порівнянні зі змінами ринкової ситуації, β = 1 оз­начає, що зміни в доходності в точності повторюють зміни в ринковій ситуації. Значення менше ніж 1 характерні для проектів з низьким рівнем ризику, чия доходність більш ста­більна, ніж ринок; значення більше ніж 1; свідчать про те, що доходи від цих проектів схильні до дуже сильного впли­ву з боку навіть незначних ринкових коливань. Хоча бета-коефіцієнт і слугує для вимірювання ризику, на практиці важко визначити його точне значення для конкретного інве­стиційного проекту. Взагалі значення β визначають виходячи з даних фондового ринку, звідки беруть відомості про доходність компанії (яка характеризується ціною її акцій).

Якщо компанія, акції якої котируються на фондовому ринку, розглядає інвестиційний проект, «типовий» для її ділової активності, то показник ризику для всієї компанії (її β)може слугувати показником рівня ризику даного конкретно­го проекту. Однак важче визначити рівень ризику проекту, який знаходиться за межами «нормальної» діяльності ком­панії. В цьому випадку можна оцінити бета-коефіцієнт про­екту, використовуючи для цього бета-коефіцієнти тих ком­паній, в чиєй сфері «нормальної» діяльності знаходиться да­ний проект. Існують, однак, дві проблеми при використанні бета-коефіцієнтів інших компаній в якості бета-коефіцієнта для конкретного проекту:

- по-перше, всі ринкові котирування засновані на вимірюванні доходу на одну звичайну акцію (тобто доходу акціонера), а не на одиницю активів (тобто доходу організації). Бета-коефіцієнт акції відображає не тільки бета-коефіцієнт активів (той що повинен використовуватися в якості заміни при оцінці проектів), але і структуру фінансів компанії. Власники акцій вважають менш надійною ту компанію, в якій на одну звичайну акцію приходиться більше запозичених коштів, і це, безумовно, відображається на бета-коефіцієнтах;

- по-друге, вплив ризику проекту на сам проект может відрізнятися від впливу ризику проекту на всю організацію в цілому, тому що даний проект є лише частиною інвестиційного портфелю фірми. Як частина інвестиційного портфелю, рівень ризику проекту визначається його співвідношенням з ризиками інших проектів у цьому портфелі.

Використовуючи β, характерний для певного типу бізне­су, в якості β окремого інвестиційного проекту можна пра­вильно визначити необхідну норму прибутку для дисконтування грошових доходів від інвестиційного проекту для виз­начення чистої дисконтованої вартості капіталовкладень.

Визначення ймовірності результатів

У сучасній економічній літературі визначають ризик, по­в'язаний з певним проектом, та ігнорується вплив цього проекту на загальну невизначеність, пов'язану з фірмою. Визначимо, наскільки деякі з методів урахування невизначе­ності, які використовують сьогодні, відповідають найкращо­му з позиції інвесторів вибору проекту. Слід відзначити, щовикористання суб'єктивних вірогідностей надає особі, що приймає рішення, найкращу картину можливостей її вибо­ру, ніж методи, що застосовуються на практиці. Оцінка імовірності того чи іншого результату інвестиційного проекту потребує, щоб особа, яка приймає інвестиційні рішення, могла б передбачити багато можливих результатів інвести­ційного проекту і була б спроможною оцінити імовірність наставання кожного з можливих варіантів. Типова ситуація, яка відображає найгірші й найкращі можливі варіанти розвитку, може включати наступні групи: «песимістичний» варіант, «найбільш можливий» і «оптимістичний».

Рішення, як правило, називають ризикованим чи невизначеним, якщо воно має декілька можливих результатів. Існує багато таких ситуацій — від будь-яких побутових си­туацій до інвестування у великі виробничі проекти. У біль­шості підходів до ризику та невизначеності передбачається не тільки знання можливих результатів будь-якого рішення, але й знання відносно можливості виникнення кожного з цих результатів з певною їхньою вірогідністю. Все це дозво­ляє визначати ризик та невизначеність, пов'язані з будь-яким конкретним рішенням з точки зору розподілу вірогід­ностей результатів. Такий розподіл показано на рис 6.1 (усі можливі чисті прибутки від проекту довготривалістю в 1 рік розташовані на горизонтальній осі, а вірогідності, пов‘язані з цими результатами, — на вертикальній).

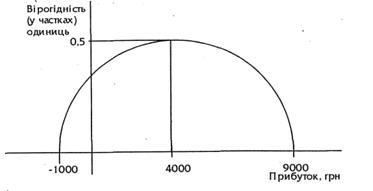Рис. 6.1. Розподіл вірогідностей одержання прибутку від проекту

На горизонтальній осі показано, що результат від реалі­зації проекту знаходиться у діапазоні від збитку 1000 грн до прибутку 9000 грн. Вертикальна вісь демонструє вірогідність будь-якого конкретного наслідку. У нашому прикладі найбільш вірогідним наслідком є одержання прибутку 4000 грн., що дорівнює 0,5. Сумарна вірогідність усіх наслідків проектуповинна дорівнювати одиниці. Виникає можливість одер­жання середнього результату П шляхом оцінки кожного можливого результату і його вірогідності та їх суми для кож­ного наслідку. Середній чистий прибуток від проекту на нашому графіку становить 4000 грн. Ця величина є середнім значенням розподілу вірогідностей проекту, її називаютьматематичним очікуванням проекту.

У таблиці 6.2 наведено приклад розрахунків для проек­ту з декількома можливими наслідками, кожен з яких є рівновірогідним. Кожна цифра у третій колонці є результатом множення доходу на його вірогідність, а сума цих цифр дає очікувану величину проекту, тобто 3250 грн.

Таблиця 6.2

Середній результат невизначеного проекту

Ризик, пов'язаний з проектом, — це можливе розход­ження результатів відносно певного значення. Ця міра ри­зику є дуже привабливою для багатьох тому, що вимір розходження результатів або дисперсії розподілу математично­го очікування вказує на вірогідне відхилення фактичного ре­зультату від його «найоптимістичнішого» прогнозу. Сутністьцього підходу наглядно показано на рис. 6.2, на якому відби­то розподіл вірогідностей результатів різних проектів.

Рис. 6.2. Невизначеність, що виміряється розходженням результатів відносно їх очікуваних значень .

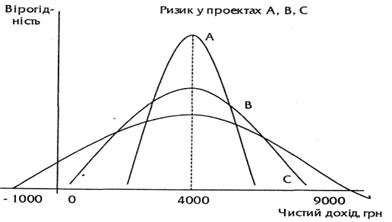Усі три проекти мають однакове математичне очікування, що дорівнює 400 грн. Проект С — це інвестиційна можливість, що відбито на попередньому графіку. Багато експертів будуть визначати проект В як менш ризикований, ніж проект С, ос­кільки крайні значення першого проекту наближені до серед­нього значення та існує більша вірогідність одержання матема­тичного очікування 4000 грн. Виходячи з наведених критеріїв можна затверджувати, що проект А є кращім за В і С.

Звичайним виміром розходження є дисперсія (V) або середньоквадратичне відхилення δ розподілу вірогідностей, які визначаються за допомогою загальновідомих формул:

; (6.1)

, (6.2)

де O- можливий результат;

Е — математичне очікування розподілу вірогідностей;

Р — вірогідність результату О.

Розходження розподілу вірогідностей результатів проекту є звичайною мірою ризику оцінки інвестиційного проекту. Пов'язана з проектом невизначеність визначається шляхом розрахунку дисперсії або середньоквадратичного відхилення.

Концепція вірогідності, що використовується у статис­тиці, базується на певній інтерпретації частот виникнення. Але ці вірогідності не можуть бути використані під час прий­няття інвестиційних рішень, які, як правило, не можна пов­торити декілька разів. Для цих випадків розроблено відпо­відну концепцію, яку назвали суб'єктивною вірогідністю.Вона дозволяє розрахувати середнє значення та середньоквадратичне відхилення для суб'єктивних розподілів вірогід­ностей. Суб'єктивна вірогідність являє собою специфічну індивідуальну думку можливостей здійснення даної події. Велика суб'єктивна вірогідність — це впевненість індивідуума в тім, що дана подія здійсниться. Однією з головних відзнак концепції суб'єктивної вірогідності від класичної є те, що у кожного індивідуума оцінка суб'єктивної вірогід­ності різноманітна. Наведемо приклад використання суб'єктивної вірогідності під час прийняття інвестиційного рішення. Окреме підприємство вирішує питання про організацію виробництва нової продукції, що потребує негайних витрат у розмірі 4000 грн на рекламу та офісні фонди. Життєвий цикл проекту планується 3 роки, при цьому обсяги продажу кожного року будуть незалежними від продажів інших років. У табл. 6.3 надано прогноз грошових потоків від проекту та вірогідність його результату.

Таблиця 6.3

Можливі результати проекту та їх вірогідність.

Очікувані значення потоків грошових коштів кожного року можуть бути використаними для розрахунку очікуваної чистої дисконтованої вартості проекту. Ця величина може бути одержана шляхом складання дисконтованих очікува­них вартостей чистих потоків кожного року, оскільки ре­зультати кожного року не залежать від результатів інших років. Для дисконтування цих коштів, як правило, викорис­товують ставку відсотка, що не враховує ризик, тобто ставка дисконту враховує тільки вартість грошей з урахуванням майбутнього періоду. Очікуєма чиста дисконтована вартість є узагальнюючим показником, але він надає небагато інфор­мації про ризикованість проекту. Одним із методів, який більш детально описує пов'язані з проектом невизначеності, є розрахунок повного розподілу вірогідностей чистої дис­контованої вартості проекту. Повний розподіл вірогідностей можливих чистих дисконтованих вартостей проекту ілюст­рує важливу картину пов'язаного з проектом ризику. Однак необхідні для цього методу розрахунки є дуже трудомістки­ми, оскільки потребують розрахунків чистої дисконтованої вартості кожного можливого результату першого року в по­єднанні з кожним можливим результатом інших років. Для полегшення цього процесу, як правило, передбачають, що має місце приблизно нормальний розподіл вірогідностей потоків грошових коштів проекту кожного року. У цьому випадку першим шагом є розрахунок середньоквадратично­го відхилення розподілу вірогідностей чистої дисконтованої вартості проекту. Для цього спочатку треба розрахувати дис­персію розподілу вірогідностей кожного потоку кожного року, використовуючи наведену вище формулу. Дисперсія першого року становить 1300000 грн, середньоквадратичне відхилення 1140 грн. Потоки інших двох років мають таку ж дисперсію і відповідне середньоквадратичне відхилення. Загальний ризик проекту можна визначити кількісно шля­хом складання дисперсій усіх років, оскільки потік кожно­го року проекту є незалежним від потоків інших років. Ступінь ризику визначається у грошах того року, у якому мають одержати відповідний потік грошових коштів, а та­кож має дисконтуватися для забезпечення можливостей по­рівняння. Для цього можна використати наступну відому формулу:

, (6.3)

де V - дисперсія чистих дисконтованих вартостей про­екту;

V - дисперсія потоків проекту і-го року.

Тоді дисперсія за нашим прикладом

V = 130000 / 1,04² +130000 /1,04⁴ +130000 / 1,04⁶ = 334100

А середньоквадратичне відхилення 1828 грн.

Маючи таку інформацію (при нормальному розподілі вірогідностей кожного року), можна розрахувати вірогідність того, що чиста дисконтована вартість нижче від певного значення. Наприклад, треба розрахувати вірогідність того, що чиста дисконтована вартість проекту знаходиться в інтервалі від математичного очікування до 1000 грн. Вірогідність виз­начається розрахунком різниці між 1000 грн та очікуваною чистою дисконтованою вартістю, яка дорівнює 773 грн, з наступним визначенням цього відхилення (227 грн) в оди­ницях середньоквадратичного відхилення. У результаті одержимо:+0,124( 227/1828). Тобто виникає можливість підрахунку вірогідності будь-якого відхилення від матема­тичного очікування на основі використання таблиці нор­мального розподілу (функції Лапласа—Гауса). Аналогічні розрахунки дають змогу розрахувати вірогідність одер­жання від проекту будь-яких можливих чистих дисконто­ваних вартостей за умови, що розподіл вірогідностей цьо­го показника є нормальним. Даний метод, як стверджує відомий західний вчений М. Бромвич, дає цінну інформа­цію про проект шляхом урахування позицій багатьох екс­пертів проекту.

Крім дослідженого випадку — коли щорічні потоки гро­шових коштів від проекту є незалежними один від одного, має місце ще й випадок — коли на результат кожного року впли­ває певний інший комплекс чинників, що діє протягом іншо­го або інших років. У цьому випадку існує значна кореляція між результатами різних років. Детальніше зупинимо увагу на випадку, коли річні потоки проекту пов'язані з позитивною лінійною кореляцією. Тобто будь-які відхилення від очікува­ної величини потоків першого року мають супроводжувати­ся аналогічним відхиленням двох інших років (у нашому прик­ладі). Формулою середньоквадратичного відхилення для гру­пи лінійно-кореляційних потоків грошових коштів є:

. (6.4)

Тобто якщо річні потоки нашого проекту мають лінійно-кореляційну залежність, тоді середньоквадратичне відхи­лення відносно математичного очікування чистої дисконто­ваної вартості дорівнює 3165.

Таким чином, можна зробити наступний висновок — лінійна позитивна кореляція потоків кожного року призводе до більшого ризику, ніж випадок з незалежними потоками. Тоді можна стверджувати, що чим вище позитивна залеж­ність між річними потоками проекту, тим він є ризиковані­шим. Але може виникнути й інша ситуація, а саме — річні витрати виробництва не залежать від результатів діяльності інших років, а річні чисті ринкові потоки лінійно корелірують (модель Хільєра). У нашому випадку хай потоки двох перших років проекту лінійно корелірують один з одним, а потік третього року є незалежним. За таких умов формулою середньоквадратичного відхилення є наступна:

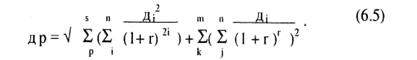Перший член під коренем є сумою дисперсій усіх неза­лежних потоків грошових коштів. Права позначка δ цього члену вказує на те, що дисперсія кожної статті розраховуєтьсяспочатку шляхом складання дисконтованих річних дис­персій потоків для кожної статті доходів чи витрат. Інша позначка δ вказує на те, що загальну дисперсію для усіх цих потоків знаходять шляхом підсумку дисконтованих дис­персій усіх елементів проекту. Другий член формули вказує на існування аналогічних операцій щодо усіх елементів про­екту, пов'язаних лінійною кореляцією. У нашому випадку потоки перших двох років слід віднести до другого типу, а потік третього року слід визначати за першим типом. Загаль­ний ризик проекту складатиме = 2430.

Отримане значення є середнім між значеннями, одержаними за умов незалежності потоків від проекту, та значеннями, одержаними за наявністю лінійно-кореляційної залежності.

Використання суб'єктивних вірогідностей дозволяє точніше урахувати ризик, ніж при використанні будь-якого іншого методу.

Аналіз сценарію

Аналіз сценарію враховує, що деякі змінні взаємозалежні та їх можна одночасно узгоджено змінювати.

За наявністю базового варіанту проекту, а також набору найбільш важливих компонентів, зміна яких визначає ризик здійснення проекту, розробляються два додаткових сценарії — «оптимістичний» і «песимістичний». У обидва сценарії закладається реалістичний набір подій. Результати аналізу зводяться в матрицю, і аналізується розподіл значень чистої поточної вартості проекту (NPV) і внутрішньої норми рен­табельності проекту (IRR).

Моделювання

Моделювання — це продовження методу оцінки ймовір­ностей можливих виходів, який був описаний вище. Метод оцінки ймовірностей включає в себе оцінку тільки одного показника — чистої приведеної вартості, але на практиці найбільша кількість факторів визначає успіх або провал інвестиційного проекту. Серед них можуть бути вартістьздійснення проекту, річний доход від капіталовкладень, норма прибутку, строк, на який розрахований проект, і його ліквідна вартість. Метод моделювання дозволяє оцінити кожен з цих параметрів з точки зору його впливу на рівень ризику проекту. При використанні методу моделювання (відомого також як «метод Монте-Карло») необхідно:

визначити ключові зміни інвестиційного проекту;

визначити всі можливі значення, які можуть приймати ці зміни;

визначити імовірність виникнення кожного значення;

збудувати модель (використовуючи комп'ютер).

Комп’ютер вибирає значення для кожного з усіх ключо­вих змінних на базі імовірності виникнення того чи іншого значення. Використовуючи ці обрані значення, машина рахує чисту приведену вартість (NVP) проекту. Після великої кількості ітерацій (цикли вирахувань) машина отримує найбільш імовірну NVP та розподіл всіх можливих її значень з вказівкою імовірності їх наступу, що дозволяє оцінити ри­зик, який зв'язаний з здійсненням даного проекту. Неваж­ка модель може бути збудована і без допомоги комп'ютера. Однак корисність моделювання залежить від комплексності вихідних даних і від кількості проведених операцій. Таким чином, на результати «ручного» моделювання навряд мож­на буде покластися.

При проведенні моделювання потрібно ураховувати взаємозалежні зміни (наприклад, ліквідаційна вартість проекту може залежати від строку, на який він розрахований). Успіх моделі цілком залежить від людей, які приймають рішення, вони повинні бути впевнені, що виявлені всі клю­чові зміни, і що кожної з них присвоєний розподіл значень залежно від імовірності їх виникнення.

Аналіз чутливості реагування

Цей метод дуже схожий на метод моделювання, але не такий важкий і глибокий. Мета аналізу чутливості — вияви­ти найважливіші фактори, так звані «критичні змінні», що здатні найбільш серйозно вплинути на проект і перевірити вплив послідовних (одиничних) змін цих факторів на результати проекту. У теорії експерименту аналіз чутливостіназивають однофакторним аналізом. Результати проведеного раніш якісного аналізу ризиків проекту є базою, фунда­ментом під час вибору факторів для кількісного аналізу.

Фактори, що вар’їрують у процесі аналізу чутливості, класифікують наступним чином:

- фактори, що впливають на обсяг доходів проекту;

- фактори, що впливають на обсяг проектних витрат.

У формуванні грошового потоку проекту, отже, і в розрахунку його критеріїв ефективності беруть участь багато факторів і позитивного (доходного), і негативного (витратного) характеру з точки зору кінцевої результативності про­екту. До позитивних факторів можна віднести затримку сплати за поставлену сировину, матеріали, комплектуючі, а також період часу поставки продукції з моменту отримання авансового платежу при реалізації продукції чи послуг на умовах передплати. Але затримка сплати за сировину має позитивний вплив на результат тільки у випадку, коли ціна матеріалів і комплектуючих визначається на дату поставки і відповідає поточному рівню цін. Важливою є група факторів, пов'язана з формуванням та управлінням запасів. Об'єктом аналізу повинні стати фактори, що характеризу­ють умови формування капіталу.

Аналіз може бути зроблено з використанням будь-яких критеріїв ефективності (прибутковості) проекту. Але результати, отримані за допомогою різних критеріїв, враховуючихтимчасову цінність грошей, тобто дисконтування, будуть співпадати.

Так, при використанні цього підходу визначаються ті фактори, які мають найбільший вплив на кінцевий результат капіталовкладень. Це досягається шляхом зміни величини однієї з ключових змінних та перерахунку NРV проекту. Якщо зміна значення змінних не виявляє суттєвого впливу на чисту приведену вартість, то правильність інвестиційного рішення не буде залежати від точного визначення значен­ня цієї змінної. Якщо навіть незначні зміни виявляють сильну дію на рівень NPV, то проект вважається «високочутливим»до значення даної зміни, оскільки цей параметр визначає ступінь ризику проекту. В цьому випадку оцінці можливих значень цієї змінної повинна приділятися увага. Там же, де змінна виявляється вирішальною для результату інвестиційного проекту і якщо ця змінна характеризується невиз­наченістю, виникає запитання: чи треба взагалі здійснювати цей проект. Таким чином, цей метод має подвійну цінність для оцінки капіталовкладень:

- дозволяє виділити ті змінні, які мають найбільший вплив на результат інвестиційного проекту і значення яких повинні бути визначені з максимальною точністю;

- допомагає виділити проект з високим ступенем ризику, обумовленим великими змінами (або невизначеністю) однієї або декількох ключових змінних, а також дозволяєрозрахувати «очікувану» NPV цих проектів.

Аналіз чутливості також є корисним в якості «попередника» моделювання, щоб оцінкам тих змінних, від яких в значному ступені залежить успіх проекту, була приділена увага при будуванні моделі.

Труднощі при застосуванні аналізу чутливості виникають, коли ключові змінні поєднані.Частково проблема може бути вирішена шляхом зведення всіх взаємопоєднанихзмінних до однієї, яка відбивала би зв'язок цих змінних.

Теорія ігор

Теорія ігор може виявлятися корисною там, де важко або неможливо визначити імовірності наступу тих чи інших подій. Теорія ігор — це консервативний підхід, направлений на мінімізацію втрат або «співчуття» від прийняття неправильних інвестиційних рішень. Незважаючи на те що підхід не може визначати краще інвестиційне рішення, він пропо­нує шляхи виключення найбільш ризикових варіантів.

Один з методів теорії ігор називається «мінімізація мак­симально можливих втрат». Цей метод допомагає обрати кращій з усіх гірших можливих виходів, які можуть виникнути, тобто він захищає від поганих варіантів. Другий метод з теорії ігор називається «мінімізація співчуття» або «мінімізація максимально можливих альтернативних витрат», який слугує для зменшення альтернативних витрат при прийнятті інвестиційних рішень.