1.4. Вибір алгоритму управління об’єктами

Динамічні властивості об’єктів управління дають змогу розробникам систем автоматики на стадії проектування ви­значити алгоритм управління. Для цього слід проаналізу­вати співвідношення між постійною часу та часом запіз­нювання. Відомо, іцо

При визначенні алгоритму управління необхідно пам’я­тати, що структура передаточної функції повинна відпові­дати виразам (1.16) та (1.17). Метод інтегральних площин дає більш складну структуру. У цьому випадку:

за передаточною функцією знаходять оригінал, за яким будують криву розгону;

крива розгону (побудована) апроксимується графічним способом, яких би динамічних властивостей не мали за­значені об’єкти;

розраховані параметри передаточної функції використо­вуються для визначення алгоритму управління.

Лінійний алгоритм управління — один із найпоширені­ших у сільськогосподарському виробництві. Він включає пропорційний, інтегральний, пропорційно-інтегральний, про- порційно-диференційований, пропорційно-інтегрально-ди- ференційований. Кожний з них має свої недоліки та пере­ваги.

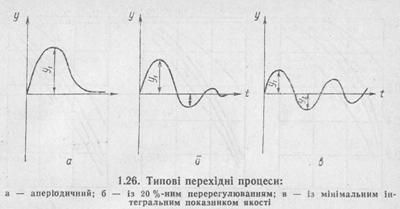
У практиці проектування для конкретного об’єкту ви­бирають такий алгоритм, який би забезпечив один із трьох типових перехідних процесів: аперіодичний, із 20 %-ним перерегулюванням, із мінімальним інтегральним показни­ком якості (рис. 1.26). Аперіодичний характеризується максимальним динамічним відхиленням, мінімальним ча­сом регулювання та відсутністю перерегулювання, із 20 %- ним регулюванням — середній по якості перехідний процес, із мінімальним інтегральним показником якості (площа

між кривою перехідного процесу та віссю часу мінімаль­на) — значним перерегулюванням, найбільшим часом ре­гулювання та мінімальним динамічним відхиленням. Кон­кретний типовий перехідний процес може бути визначений з урахуванням вимог технологів до відповідного об’єкту уп­равління.

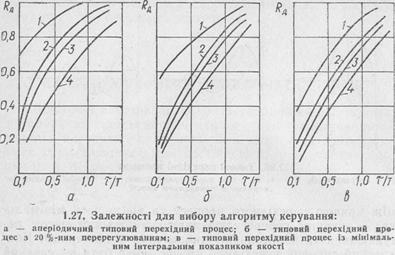
Методика вибору найкращого алгоритма управління полягає у визначенні динамічного коефіцієнта регулюван­ня. Для статичних об’єктів:

де у\ — максимальне динамічне відхилення; k₀—коефіці­єнт передачі об’єкта управління; у_м— максимально мож­ливе збурення по навантаженню (у відсотках переміщен­ня регулюючого органу).

Після цього за графічними залежностями (рис. 1.27) визначають алгоритм управління.

Для астатичних об’єктів:

де 8о — швидкість розгону об’єкта; т — час запізнювання.

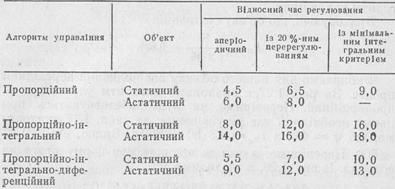
Для астатичного об’єкта алгоритм управління знахо­дять за табл. 1.16.

Для того, щоб переконатись у правильності вибору ал­горитму управління, розраховують час регулювання, який потім порівнюють із вимогами технологів:

де -ф — відносний час регулювання, що вибирається за табл. 1.17.

Для статичних об’єктів відносний час регулювання при інтегральному алгоритмі управління знаходять за допо­могою графічних залежностей (рис. 1.28).

Якщо виявиться, що пропорційний алгоритм управління найкращий, у цьому випадку слід визначити статичну по­хибку та порівняти її з допустимою:

де А у — статична похибка; /г_Р, /г — відповідно коефіцієнти передачі регулятора та об’єкту; 5 — коефіцієнт етатизму.

Проте скористатись виразом (1.47) важко, тому що £_р — невідомий (регулятор ще не вибраний). Тому реко­мендується знайти А у за графічними залежностями (рис. 1.29).