3.1. Модель поверхні Землі та її розміри

Форма Землі як планети обумовлена дією багатьох процесів, що пов’язані з її утворенням та існуванням. При розв’язанні топографо- геодезичних задач та при картографуванні земної поверхні необхідно її фо­рму описати найбільш достовірною моделлю з установленими розмірами.

Земля не є правильною геометричною фігурою. В зв’язку з тим, що фізична поверхня Землі становить сполучення материків й водних просто­рів, її неможливо виразити ні однією з відомих й математично вивчених геометричних фігур. Всю поверхню Землі можна розділити на дві нерівні частини: океани з відкритими морями, що утворюють єдиний водний про­стір, який займає 71% поверхні Землі, та материки, що складають 29%. Рі­вень поверхні океанів та з'єднаних з ними морів приблизно однаковий, але їх дно і поверхня Землі являють собою різноманітне поєднання нерівнос­тей в вигляді височин і впадин.

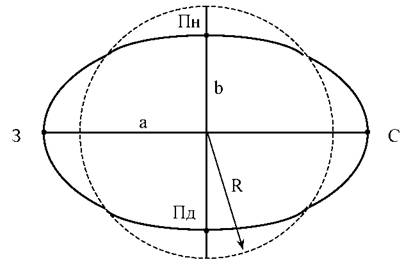
За даними геофізики, Земля в значній своїй товщі під впливом без­перервно діючих на неї сил поводить себе як пластичне тіло. В зв'язку з цим до неї, за винятком материкового тонкого верхнього шару, що є зем­ною корою, можна застосувати закони гідростатики. Якби Земля була од­норідним тілом, постійно знаходилась в нерухомому стані й підлягала би дії тільки внутрішніх сил тяжіння, то вона являла б собою кулю (рис. 3.1).

Оскільки Земля обертається навколо своєї осі з постійною швидкіс­тю, то під дією відцентрових сил вона прийняла би форму, що сплюснута в напрямку до полюсів, тобто форму сфероїда або еліпсоїда обертання (рис. 3.1). Така форма сфероїда отримується при обертанні еліпса навколо його малої осі. Це теоретично довів у 1687 р. І. Ньютон в своєму творі "Математичні принципи натуральної філософії" на основі відкритого ним закону тяжіння. Вперше помітив, що Земля не ідеальна куля, французький вчений Ш. Ріше в 1672 році під час астрономічних спостережень.

Поверхня такої еліпсоїдальної Землі, як фігури рівноваги, була би скрізь горизонтальною, якби в кожній її точці напрямок сили тяжіння збі­гався би з напрямком нормалі, тобто лінії, що перпендикулярна дотичній в даній точці до поверхні еліпсоїда. Поверхні, перпендикулярні в кожній то­чці до напрямку прямовисної лінії (напрямку сили тяжіння), називаються рівневими поверхнями сили тяжіння.

В дійсності, під дією процесів, що пов'язані з утворенням та життям Землі як планети, внутрішня її будова неоднорідна. Земля має декілька ша­рів, щільність яких збільшується в напрямку до центра. В зовнішньому шарі Землі товщиною від 6 до 70 км, що називається літосферою, законо­мірностей в розподілі щільності немає. Це пояснюється розміщенням літо­сфери на межі між твердою Землею, гідросферою та атмосферою. В ній без особливих перешкод відбуваються переміщення порід під дією внутрішніх й зовнішніх сил. В результаті утворюється фізична (топографічна) поверх­ня Землі, що являє собою поєднання материків й океанічних впадин з складними геометричними формами. Найвища точка Земної поверхні роз­міщена в Гімалайських горах. Пік Евереста на горі Джомолунгма стано­вить 8848 м над рівнем світового океану. Найнижча точка глибиною 11022 м розміщена в Маріанській впадині Тихого океану. На Україні най­вища точка - в Карпатах, гора Говерла, має висоту 2061 м, а найбільша глибина Чорного моря - 2021 м.

Під дією нерівномірно розміщених мас в земній корі змінюється на­прямок сил тяжіння. Рівнева поверхня Землі, яка перпендикулярна до на­прямку сили тяжіння, відхиляється від еліпсоїдальної. Вона стає складною й неправильною в геометричному відношенні. Оскільки на Землі водні простори займають більшу площу, то рівнева поверхня збігається з водною поверхнею океанів і морів, що знаходяться в спокійному стані, і не вира­жається будь-якою з відомих аналітичних форм. Німецький фізик І. Лістінг в 1873 році запропонував для позначення форми Землі термін геоїд, що не має ніякого геометричного змісту.

Геоїдом називають геометричне тіло, що обмежене рівневою повер­хнею, яка збігається з поверхнею морів та океанів при спокійному стані водних мас й уявно продовженою під материками таким чином, щоб на­прямки сил тяжіння перетинали її під прямим кутом.

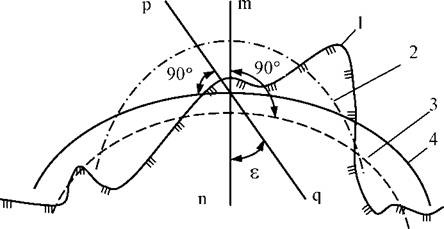
Маси в земній корі розміщені нерівномірно, тому прямовисні лінії сил тяжіння відхиляються в сторону більш щільних притягуючих мас від напрямків, які займали б вони, якби Земля була однорідною. Отже, повер­хня геоїда, що скрізь перпендикулярна напрямкам прямовисних ліній, буде мати складну, неправильну форму з кривиною, що змінюється. Особливо різкі зміни кривини поверхні геоїда спостерігаються біля підніжжя гірсь­ких хребтів, поблизу берегових ліній морів. Кут є між нормаллю тп в даній точці (рис. 3.2.) і напрямком прямовисної лінії pq до поверхні еліп­соїда називають схиленням прямовисної лінії.

В середньому для земного сфероїда схилення прямовисної лінії дорі­внює 3"-4" і тільки в деяких місцях воно досягає декількох минут. Макси­мальне відхилення поверхні геоїда від еліпсоїда не перевищує 150 м. Для математичної обробки геодезичних вимірювань необхідно знати форму поверхні Землі. Прийняти з цією метою фізичну поверхню або геоїд немо­жливо, оскільки ці поверхні не можна описати ні однією з математичних формул. Дослідження показали, що найбільш близькою до геоїда матема­тичною поверхнею є еліпсоїд обертання, тому для складання карт й прове­дення необхідних вимірювань та розрахунків, що пов'язані з визначенням місцеположення точок на земній поверхні, Землю вважають приплюсну­тою кулею, яка має вигляд еліпсоїда обертання, що називається земним еліпсоїдом. Його розміри та форма (рис. 3.1.) характеризуються парамет­рами: довжиною великої (екваторіальної) - а та малої (полярної) - Ь пів­осей, коефіцієнтом полярногостиснення а та ексцентриситетами е і С

Протягом трьох останніх століть вчені різних країн, використовуючи різні дані вимірювань, обчислювали розміри земного еліпсоїда. В нашій

Земний еліпсоїд з визначеними розмірами відповідно орієнтований в тілі Землі так, щоб його поверхня найближче підходила до поверхні геоїда, називають референц-еліпсоїдом.

Фізична поверхня Землі, на якій виконують геодезичні вимірювання, значною мірою відрізняється від референц-еліпсоїда. При топографічних й картографічних роботах Землю часто приймають за кулю, об’єм якої дорі­внює об’єму земного сфероїда. Радіус такої кулі визначають за формулою:

Виходячи з розмірів референц-еліпсоїда Ф.Н. Красовського, радіус Землі Я = 6371,11 км. Для незначних ділянок земної поверхні поверхню еліпсо їда приймають за площину.