4.6. Система плоских прямокутних координат Гаусса-Крюгера

Система географічних координат може бути розповсюджена як єди­на координатна система на поверхню земного еліпсоїда. Але використання географічної системи координат пов’язане з певними труднощами, серед яких:

а) взаємне розміщення пунктів визначається в кутових величинах, а всі відстані на місцевості вимірюють в лінійній мірі;

б) значення одних і тих же кутових одиниць відповідає різним ліній­ним величинам в залежності від широти;

в) використання географічних координат вимагає складних й трудоміс­тких, навіть для малих відстаней, обчислень.

Для зображення на плоскому аркуші паперу земної поверхні викори­стовують метод прямокутних (ортогональних) проекцій. В ортогональних проекціях зображають просторовий об'єкт на площині за допомогою прое­кційних променів, що перпендикулярні до площини проектування.

Земну сферу неможливо розгорнути в площину. Тому для зображен­ня значних ділянок земної поверхні на площині використовують спеціальні проекції, що дозволяють перенести точки поверхні Землі на площину за відповідними математичними законами.

В топографії найбільшого розповсюдження отримала рівнокутна (конформна) проекція, оскільки в разі врахування спотворення необхідно вводити практично однакові поправки в довжину ліній в межах окремих ділянок.

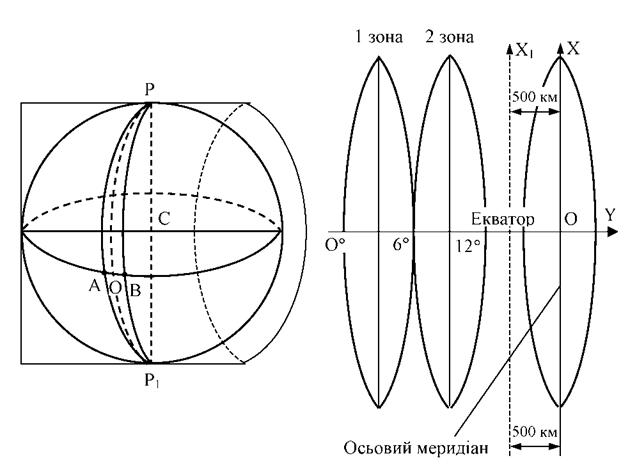
В Україні прийнята рівнокутна поперечно-циліндрична проекція сферичної поверхні на площині і відповідна до неї система координат Га­усса-Крюгера (Гауссзапропонував цю проекцію, а Крюгер розробив фор­мули для її використання в геодезії) (рис.4.7).

З метою збереження на аркуші карти практично одного масштабу й по­дібності зображення на ньому деталей місцевості земний еліпсоїд за допомо­гою меридіанів ділять на 60 шестиградусних зон. Рахунок зон ведуть на схід від Грінвічського меридіана. Середній меридіан зони називають осьовим.

Кожну таку зону (РАР₁В) проектують на поверхню дотичного до неї по осьовому меридіану (РОР₁) циліндра, вісь якого проходить через центр земного еліпсоїда перпендикулярно до площини осьового меридіана. Кож­на з цих 60 зон зображається на площині незалежно від решти. Кожну зону на поверхню циліндра проектують так, щоб після розгортання поверхні циліндра в площину, зображення малого контуру навколо кожної точки на циліндрі було б подібне відповідному контуру на площині. За цієї умови кути між відповідними напрямками на еліпсоїді будуть рівні між собою. Осьовий меридіан кожної зони та екватора зображується на проекції пря­мою лінією без спотворення.

За початок координат в кожній зоні приймають перетин осьового меридіана й екватора. За вісь абсцис Х приймають осьовий меридіан, а за вісь ординат У - екватор.

Спотворення довжин ліній збільшується в міру віддалення від осьо­вого меридіана пропорційно квадрату ординати. Ці спотворення на межі

де Уі, у₂ - ординати кінцевих точок лінії довжиною ه; я - середній радіус кривизни.

Система координат в кожній зоні однакова. Для встановлення зони, в якій знаходиться точка за даними координатами, ліворуч від значення ор­динати пишуть номер зони. Щоб не було від’ємних ординат, точкам осьо­вого меридіана умовно дописується ордината, що рівна 500 км (рис.2.9). Тоді всі точки на схід й захід від осьового меридіана будуть мати позитив­ні ординати. Наприклад, якщо ордината у = 4 312 142, то точка знаходить­ся в четвертій зоні і віддалена на захід від осьового меридіана на

312 412 - 500 000= - 187858 м.

Довготу осьових меридіанів шестиградусних зон визначають за фор- мул©ю

де п - номер зони.

Для полегшення користування прямокутними координатами в кож­ній з оні розбивають кілометрову сітку.