11.3.3. Обчислення координат точок теодолітного полігону

Обчислення координат точок теодолітного полігону включає ряд опе­рацій, що їх виконують в обумовленій послідовності. Вихідними даними для обчисленнякоординат є горизонтальні кути в вершинах полігону, ди- рекційний кут початкового напряму та горизонтальні проекції сторін тео­долітного ходу.

Відхилення суми виміряних кутіввід теоретичноїобчис­люють за формулою

Теоретична сума кутів многокутника, що описує замкнутий теодоліт­ний хід:

де- кількість кутів теодолітного ходу.

Кутова нев'язка не повинна перевищувати граничну величину:

Якщо кутова нев'язка виявиться допустимою, тобто меншою від гра­ничної або рівною їй, то у виміряні кути вносять поправку з оберненим знаком нев’язки:

У першу чергу поправки вносять у кути, обмежені короткими сторо­нами, бо в цьому випадку особливо позначається вплив неточного центру­вання теодоліта і встановлення віхи у вершині кута. Ув'язування кутів контролюють, порівнюючи суми в ипр авлених і теоретичних кутів:

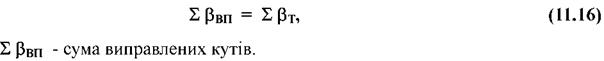
Після ув'язування виміряних кутів обчислюють дирекційні кути, ви­користовуючи значення початкового дирекційного кутаі виправлених кутівтеодолітного ?،оду

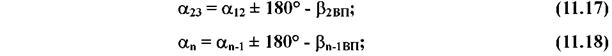
де- дирекційні кути, відповідно, першого й другого на­

пряму, наступної і попередньої сторони;

- виправлені кути, відповідно, на другій вершині та між по­передньою і наступною сторонами теодолітного ходу.

Із дирекційних кутіввіднімають 180°, якщо різниця (- ) більша. Якщо різницяменше, то до неї до­

дають 180°.

Контролем обчислення дирекційних кутів теодолітного полігону є одержання у кінці обчислення дирекційного кута першого напряму

де- дирекційний кут останньої сторони ходу;

- виправлений кут на першій вершині полігону.

За дирекційними кутами сторін теодолітного ходу обчислюють рум­би. За відомими румбами сторін теодолітного полігону г і горизонтальни­ми проекціями ліній ёобчислюють приріст координат, м,

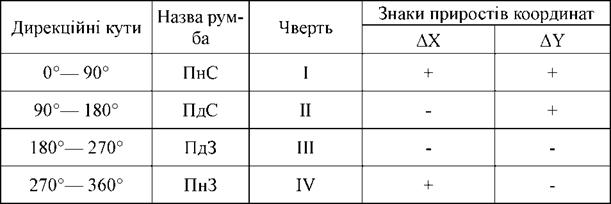
Знаки приростів координат залежать від напряму сторони теодоліт­ного ходу, тобто величини дирекційного кута, або назви румба (табл. 11.10).

У замкнутому ході сума приростів координат по осі X та по осі У те­оретично повинна дорівнювати нулю.

Практично ж через неминучі похибки при вимірюванні, особливо сторін теодолітного ходу, вона не дорівнює нулю. Тоді алгебраїчна сума приростів координат по осі абсцис та осі ординат буде нев’язкою в відпові­дних приростах коор динат

Абсолютну нев'язку в приростах координат обчислюють за форму­лою, м,

де— нев’язки в відповідних приростах координат, м.

Поділивши абсолютну нев'язку на суму сторін замкнутого теодоліт­ного ходу, дістають відносну нев'язку, яка характеризує точність вико­нання польових вимірювань, м,

Якщо відносна нев'язка теодолітного ходу менше допустимої:

то обчислені приростикоординат виправляють по осіна величину, а по осіна величину.

Поправки вводять в прирости координат з оберненим знаком пропор­ційно довжинам,

Поправки округлюють до 0,01 м і записують зверху обчислених при­ростів координат. Знайдені поправки алгебраїчно підсумовують з відповід­ними координатами і отримують виправлені прирости координат. Сума ви­правлених приростів для теодолітного полігону повинна дорівнювати нулю:

За виправленими приростами координат від початкової точки з відо­мими координатами послідовно обчислюють координати всіх точок ходу за формулами, м:

Контроль обчислень координат полягає у тому, що у кінці обчислень мають знову одержати коорд^инати початкової точки

де- координати і відповідні їм прирости координат кі­нцевої точки, м.