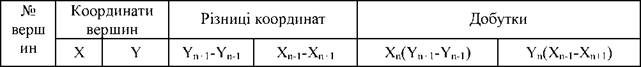Аналітичний спосіб

Обчислення площ за координатами вершин полігону застосовується коли полігон має складну форму багатокутника, границі якого прямолінійні і відомі координати його вершин. Для виведення відповідних формул візьмемо простий замкнений полігон у вигляді трикутника АВС, координати вершин якого відомі.

В загальному випадку це рівняння виразиться такою формулою:

і читається так: подвійна площа багатокутника дорівнює сумі послідовних добутків абсцис (іксів) на різницю ординат (ігреків) наступної та попередньої по відношення до абсциси.

Якщо праву частину рівняння згрупувати по у (ігреках), то формула прийме вигляд:

і читається так: подвійна площа багатокутника дорівнює сумі послідовних добутків ординат (ігреків) на різницю абсцис (іксів) попередньої і наступноїпо відношення до ординати.

Звичайно результати обчислення площі по обох формулах мають бути однаковими.

Цей спосіб є найбільш точним, бо помилка у визначенні площі залежить тільки від помилок вимірювань на місцевості. Наближено вважається, що відносна помилка визначення площі дорівнює подвійній відносній помилці вимірювання ліній, наприклад, для середніх умов вимірювання ліній мірною стрічкою відносна помилка дорівнює 1:2 000, тоді відносна помилка визначення площі буде 1:1

0. Основний недолік способу - складність обчислень. Тому в сучасних умовах для визначення площ полігонів, особливо з великою кількістю вершин, застосовують комп’ютери, в пам’ять яких занесено формули. Оператори вводять у комп’ютер координати точок (вершин полігона) і за лічені хвилини дістають площу полігона. із занесенням результатів у спеціальну відомість (табл.).