6.9. Ряди переважальних чисел

Ряди переважальних чисел складають зазвичай за геометричною прогресією, що характеризується сталим відношенням між двома сусідніми числами. Наприклад, для множника 2 отримують ряд чисел 1; 2; 4 ; 8; 16; 32 тощо. Добуток чи частка від ділення будь- яких членів геометричної прогресії (ряду) завжди також є її членом. Наприклад, 2 • 4 = 8; 8 • 4 = 32; 16 : 8 = 2; 32 : 4 = 8 тощо. Будь-який член прогресії, піднятий до цілої додатної чи від’ємної степені, також є її членом. Наприклад,У зв’язку з цим величини, що визначаються як добутки, частки, підне­сення до цілої степені, також є членами прогресії. Наприклад, якщо лінійні розміри взято із ряду (прогресії), то і площі та об’єми фігур також є членами ряду.

Найпоширенішими геометричними прогресіями, відповідно до з ГОСТу 8032-84, є прогресії, що мають число 1 і множник <р„ = ^10 . Згідно з рекомендаціями 180, встановлено чотири основні десяткові ряди переважальних чисел з множниками відповідно для рядів:

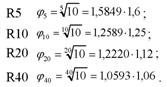
Для особливих випадків, за наявності обґрунтування, допустимо використання рядута всіх похідних рядів, що отримані з основнихшляхом добору з них кожного другого, третього тощо членів ряду. Допускається створювати ряди, які для різних діапазонів мають неоднакові множники. Згідно з рекомендаціями, у науці, техніці та виробництві допускаються заокруглення значень окремих членів рядів.

Перевагу завше віддають рядам з більшим множником, а використання рядів з меншими множниками потребує відповідного технічного та економічного обґрунтування. Ряди переважальних чисел рекомендовані для добору номінальних значень параметрів усієї продукції, що сприяє взаємоузгодженню параметрів виробів та їх складових частин (матеріалів, заготовок, напівфабрикатів, ком­плектувальних виробів тощо).

Значно рідше для стандартизації параметрів виробів використовують ряди, складені на основі арифметичних прогресій, для яких харак­терним є те, що стала величина являє собою різницю між будь-якими двома сусідніми числами. Наприклад, 1; 2; 3; 4; 5; .., 25; 50; 75; 100; 125; .., де різниці для першого та другого рядів становлять відповідно 1 і 25. Значно рідше застосовують так звані ступінчасто- арифметичні ряди, що складаються з окремих частин різних рядів. Наприклад, ряд діаметрів метричної різі: 1; 1,1; 1,2; 1,4; 1,6; 1,8; 2,0; 2,2; ...; 3; 3,5; 4; 4,5; ...; 135; 150; 155; 160 тощо. У радіотехніці використовують переважальні числа із рядів Е, встановлених ІЕС, наприклад, ряд ЕЗ із множником; ряд Е12 із множником ; ряд Е6 із множником; ряд Е24 із множ­ником.