6.1. Суть та умови використання середніх величин. Види середніх величин

У статистиці середня величина є найбільш розповсюдженою формою узагальнюючого показника, оскільки він дає кількісну характеристику масових соціально-економічних явищ та процесів.

Середня величина – це узагальнена характеристика однорідної сукупності за варіюючою ознакою, що показує типовий рівень цієї ознаки у одиниці сукупності.

Характерний, типовий рівень ознаки формується під впливом так званих систематичних (невипадкових, постійних) факторів, а відхилення індивідуальних значень від типового рівня зумовлені дією випадкових факторів, котрі впливають по-різному на окремі одиниці сукупності. Таким чином, середня величина відображає те спільне, загальне, що є характерним для усіх одиниць досліджуваної сукупності.

З допомогою середніх величин вирішуються наступні завдання статистичного дослідження:

характеристика досягнутого рівня розвитку явища або процесу;

порівняння показників, обчислених  по різних сукупностях;

характеристика розвитку (варіації) явища у часі та просторі;

вивчення взаємозв`язку між показниками.

При визначенні середньої величини необхідно дотримуватись двох головних вимог: по-перше, сукупність повинна бути якісно однорідною; по-друге, достатньо велика кількість одиниць у сукупності, тобто наявність масових даних. Бажано, щоб при визначенні середньої величини враховувалися значення показника по усіх одиницях сукупності.

Середні величини поділяються на загальні та групові. Загальна середня величина характеризує сукупність в цілому, а групова – окрему групу одиниць. Якщо сукупність складається з якісно різнорідних груп, загальна середня величина не буде типовою характеристикою сукупності, тому обов`язково необхідно визначати групові середні величини. Наприклад, при вивченні витрат на підготовку фахівців необхідно враховувати наявність різних форм навчання: денної, заочної та вечірньої.

За методикою розрахунку всі середні величини, які використовуються у статистиці, відносяться до класу степеневих середніх, формула якої в загальному має вигляд:

,

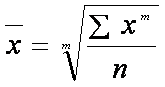де х – індивідуальні значення ознаки; n – чисельність сукупності (кількість одиниць).

                В залежності від значення показника степеня m розрізняють такі середні величини:

                m = -1  - середня гармонійна;

                m = 0  - середня геометрична;

                m = 1  - середня арифметична;

                m = 2  - середня квадратична.

При використанні середніх величин основним питанням є вибір виду середньої, при цьому визначальним фактором є відповідність обчислень економічній суті осереднюваного показника та характеру вихідних даних.