6.2. Середня арифметична величина: методика розрахунку та властивості
Середня арифметична величина є найбільш поширеним видом середньої. Вона використовується у тому випадку, коли обсяг варіюючої ознаки одержується як сума індивідуальних значень. Середня арифметична величина має таку загальну логічну формулу розрахунку:
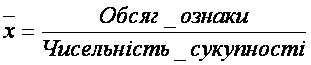 .
.
У тому випадку, коли середня величина визначається на основі індивідуальних, тобто незгрупованих даних, використовується формула середньої арифметичної простої:
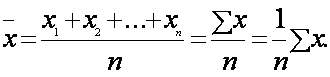
Наприклад, відомий рівень місячної оплати за житлово-комуальні послуги 12 сімей: 286, 378, 183, 295, 363, 280, 276, 292, 358, 265, 275, 373 грн. Середній рівень оплати становить:
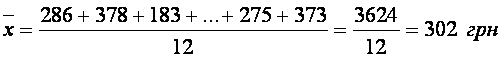
Якщо вихідні дані є результатом групування, тобто відомий дискретний або інтервальний ряд розподілу, використовується формула середньої арифметичної зваженої:
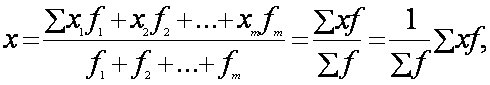
де х – варіанти; f – частоти; m – число груп.
Наприклад, відомий дискретний ряд розподілу пацієнтів за терміном їх госпіталізації у днях:
| Число днів госпіталізації (х) | Число пацієнтів (f) | xf |
| 8 | 2 | 16 |
| 9 | 5 | 45 |
| 10 | 9 | 90 |
| 11 | 12 | 132 |
| 12 | 10 | 120 |
| 13 | 11 | 143 |
| 14 | 8 | 112 |
| 15 | 5 | 75 |
| 16 | 1 | 16 |
| 19 | 1 | 19 |
| Разом | 64 | 768 |
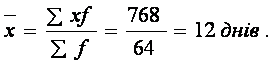
У багатьох випадках вихідні дані для визначення середньої арифметичної являють собою інтервальний ряд розподілу. Тоді спочатку інтервальний ряд розподілу перетворюється у дискретний шляхом знаходження середини кожного інтервалу, а далі розрахунок здійснюється як у попередньому випадку за формулою середньої арифметичної зваженої.
Наприклад, відомий ряд розподілу за розміром штрафу:
| Розмір штрафу, грн. | Число штрафів (f) | Середина інтервалу (х) | xf |
| До 100 | 4 | 50 | 200 |
| 100 – 200 | 20 | 150 | 3000 |
| 200 – 400 | 26 | 300 | 7800 |
| 400 – 600 | 15 | 500 | 7500 |
| 600 – 800 | 8 | 700 | 5600 |
| 800 – 1000 | 3 | 900 | 2700 |
| 1000 – 2000 | 2 | 1500 | 3000 |
| 2000 – 3000 | 2 | 2500 | 5000 |
| Разом | 80 | х | 34800 |
Середній розмір штрафу:
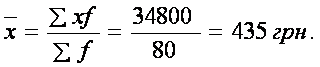
Якщо вихідні дані являють собою результат групування і відомі середні значення показника по кожній групі (групові середні), то розрахунок загальної середньої здійснюється виключно за формулою середньої арифметичної зваженої:
![]()
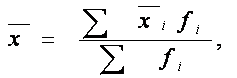
де ![]() - групові середні величини;
- групові середні величини; ![]() –число одиниць у і-тій групі.
–число одиниць у і-тій групі.
Наприклад, групування вкладників за розміром вкладу:
|
| Середній розмір вкладу, грн. | Число вкладників, чол. |
|
| Невеликий | 2300 | 2130 | 4899000 |
| Середній | 5700 | 650 | 3705000 |
| Великий | 14200 | 97 | 1377400 |
| Разом | х | 2877 | 9981400 |
Загальна середня дорівнює:
![]()
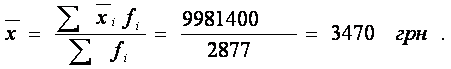
Середня арифметична величина має ряд властивостей, що використовуються при обчисленнях:
При збільшенні або зменшенні кожної частоти в к разів, середня не зміниться.

2. При збільшенні або зменшенні кожної варіанти в к разів середня зміниться в стільки ж разів.
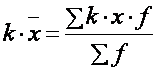 або
або ![]()
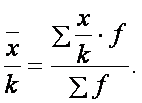
3. При збільшенні або зменшенні кожної варіанти та сталу величину А, середня зміниться на цю ж величину.
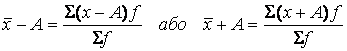
4. Сума відхилень значень ознаки (варіант) від середньої арифметичної дорівнює нулю:
![]()
5. Середня арифметична, що помножена на чисельність сукупності, дорівнює обсягу ознаки.
![]()
6. Сума квадратів відхилень варіант від середньої арифметичної є мінімальною величиною із всіх можливих.
![]()
Властивість 1 свідчить про те, що середню арифметичну можна визначити як за абсолютними, так і за відносними частотами.
Властивості 2 та 3 використовуються для спрощення підрахунків середньої арифметичної зваженої в інтервальних рядах розподілу (метод «моментів»). Середнє значення при використанні цього методу визначається за формулою:
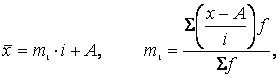
де: m1 — момент першого порядку;
і — величина інтервалу;
А — середина інтервалу з найбільшою частотою.
