6.3. Середня гармонійна величина
Середня гармонійна величина використовується у тому випадку, якщо відомі обернені значення осереднюваного показника. У цьому разі
, де х — значення прямого (осереднюваного) показника,
— значення оберненого показника.
Наприклад, прямий показник — продуктивність праці. а обернений — трудоємкість. Отже, якщо відомі значення трудоємкості, то для розрахунку середньої продуктивності праці необхідно застосувати середню гармонійну величину.
Для індивідуальних (незгрупованих) даних використовується середня гармонійна проста:
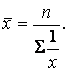
Для рядів розподілу застосовують середню гармонійну зважену:
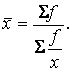
Частіше при розрахунках середньої величини використовується середня гармонійна у вигляді:
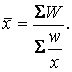
де: W = хf — значення об’ємного показника;
х — значення осереднюваного показника.
Остання формула застосовується у тих випадках, коли частоти у явній формі невідомі, а є готові добутки варіант і частот (W = xf). Наприклад, відома ціна одиниці товару та його вартість, а кількість проданих одиниць невідома. Розглянемо приклад обчислення середньої гармонійної зваженої.
| Цех | Зарплата працівника, грн. (х) | Фонд зарплати цеху, грн. (W = xf) |
| 1 | 282 | 118900 |
| 2 | 364 | 53120 |
| 3 | 258 | 17980 |
| Разом | х | 190000 |
Середня зарплата одного працівника по трьох цеха разом:
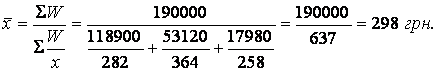
Таким чином, необхідно пам’ятати, що середня арифметична зважена використовується тоді, коли відомі значення варіант (х) та частот (f). Якщо ж замість частот відомі обсяги ознаки, тобто значення W = xf , необхідно скористатися середньою гармонійною зваженою. Але у будь-якому випадку розрахунки повинні відповідати логічній формулі середньої величини.